Find-number-of-4-letter-words-which-can-be-formed-using-the-letters-of-the-word-ALLAHABAD-such-that-NO-repetition-of-letter-and-word-should-start-either-from-H-or-ends-with-D-

Question Number 49482 by rahul 19 last updated on 07/Dec/18

F i n d n u m b e r o f 4 - l e t t e r w o r d s w h i c h

c a n b e f o r m e d u s i n g t h e l e t t e r s o f

t h e w o r d^{'} {A L L A H A B A D}^{'} s u c h t h a t :

N O r e p e t i t i o n o f l e t t e r a n d w o r d s h o u l d

s t a r t “ {e i t h e r}^{″} f r o m H “ {o r}^{″} e n d s w i t h D ?

Commented by tanmay.chaudhury50@gmail.com last updated on 07/Dec/18

w h a t i s t h e a n s w e r \dots

Commented by rahul 19 last updated on 07/Dec/18

I^{'} m c o n f u s e d i n t h e l a n g u a g e o f t h e

p r o b l e m \dots .

I f a w o r d s t a r t s f r o m H a n d e n d s w i t h

D . I s t h i s c a s e a c c e p t a b l e ? ?

Commented by Kunal12588 last updated on 07/Dec/18

t h e r e a r e 5 l e t t e r s A, L, H, B, D (r e p e t i o n n o t a l l o w e d)

w e h a v e t o m a k e 4 l e t t e r w o r d s i n w h i c h o n e

l e t t e r i s f i x e d . S o w e a c t u a l l y h a v e t o m a k e

3 l e t t e r w o r d s w i t h r e m a i n i n g l e t t e r s .

w h i c h i s^{4} P_{3} = \frac{4!}{(4 - 3)!} = 4! = 24 w o r d s .

Commented by Kunal12588 last updated on 07/Dec/18

i f t h e 4 l e t t e r s t a r t s w i t h H a n d e n d s w i t h D

t h e n i n t h e 4 l e t t e r w o r d 2 p l a c e s a r e f i x e d . W e

h a v e t o a r r a g e r e m a i n i n g 2 p l a c e s w i t h

r e m a i n i n g 3 l e t t e r s .

n o . o f w o r d s =^{3} P_{2} = 6

w h i c h a r e

H A L D, H A B D, H L A D, H L B D, H B A D, H B L D

Commented by Kunal12588 last updated on 07/Dec/18

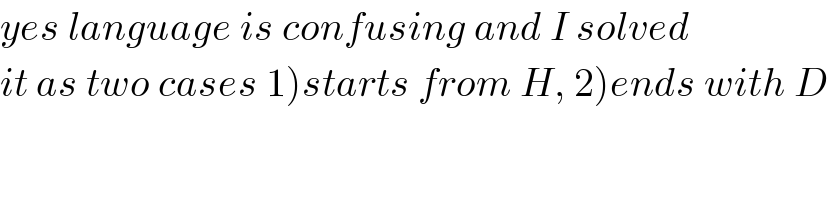
y e s l a n g u a g e i s c o n f u s i n g a n d I s o l v e d

i t a s t w o c a s e s 1) s t a r t s f r o m H, 2) e n d s w i t h D

Commented by Kunal12588 last updated on 07/Dec/18

24 i t h i n k

Commented by rahul 19 last updated on 07/Dec/18

C o r r e c t a n s w e r i s 42 (i n c l u d i n g t h e

c a s e s w h e n l e t t e r s t a r t f r o m H & e n d s

w i t h D) .

Commented by rahul 19 last updated on 07/Dec/18

thank you sir!�� Sir, but why have you counted the cases in which word starts from H and ends with D ... That's my query.

Commented by tanmay.chaudhury50@gmail.com last updated on 07/Dec/18

i a m a s k i n g t h e f i n a l r e s u l t s n o t t h e m e t h o d s \dots

Commented by mr W last updated on 07/Dec/18

t h e a n s w e r i s 2 \times 4! - 3! = 42

w e h a v e 5 d i f f e r e n t l e t t e r s .

f o r w o r d s s t a r t i n g w i t h H t h e r e a r e

4 \times 3 \times 2 = 4! p o s s o b i l i t i e s

f o r w o r d s e n d i n g w i t h D t h e r e a r e

a l s o 4! p o s s o b i l i t i e s, b u t s o m e o f t h e m

s t a r t w i t h H w h i c h a r e a l r e a d y c o u n t e d .

n u m b e r o f w o r d s s t a r t i n g w i t h H a n d e n d i n g w i t h

D i s 3 \times 2 = 3!

\Rightarrow s o l u t i o n i s 2 \times 4! - 3! = 42

Commented by Kunal12588 last updated on 07/Dec/18

g o d b l e s s y o u s i r

Commented by mr W last updated on 07/Dec/18

y e s . i h a v e c o u n t e d a l s o w o r d s s t a r t i n g

w i t h H a n d e n d i n g w i t h D . i t h i n k

t h e q u e s t i o n m e a n s w o r d s s t a r t i n g

w i t h H, n o m a t t e r i f t h e y e n d w i t h D

o r n o t, o r w o r d s e n d i n g w i t h D, n o

m a t t e r i f t h e y s t a r t w i t h H o r n o t .

Commented by mr W last updated on 07/Dec/18

i t h i n k t h e l a n g u a g e i s q u i t e c l e a r :

e i t h e r c o n d i t i o n 1 o r c o n d i t i o n 2

m e a n s o n e o f t h e c o n d i t i o n s

m u s t b e f u l f i l l e d . i t {d o e s n}^{'} t r e j e c t

t h a t b o t h c o n d i t i o n s a r e f u l f i l l e d . i f

i t i s n o t a l l o w e d t h a t b o t h c o n d i t i o n s

a r e f u l f i l l e d, t h e n t h e q u e s t i o n h a s

h a d t o b e :

e i t h e r c o n d i t i o n 1 o r c o n d i t i o n 2, b u t

n o t c o n d i t i o n 1 a n d c o n d i t i o n 2 t o g e t h e r

Commented by rahul 19 last updated on 07/Dec/18

thank you so much sir!��

Answered by tanmay.chaudhury50@gmail.com last updated on 07/Dec/18

A = 4 B = 1 D = 1 H = 1 L = 2

1) w o r d s s t a r t w i t h H

\underset{1}{H} \underset{2}{-} \underset{3}{-} \underset{4}{-}

s e l e c t i o n o f a l p h a b e t

o n e A f r o m 4 A

o n e B f r o m 1 B

o n e D f r o m 1 D

o n e L f r o m 2 L

s o v a c a n t p l a c e t h r e e (03) b u t a v a i l a b l e a l p h a b e t

(A, B, D, L) s o p e r m u t a t i o n = 4 \times 3 \times 2 = 24

(s t a r t b y H e n d b y D) + (s t a r t b y H e n d b y o t h e r s) = 24

2) w o r d s e n d w i t h D

\underset{1}{-} \underset{2}{-} \underset{3}{-} D

o n e A f r o m 4 A

o n e B f r o m 1 B

o n e H f r o m 1 H

o n e L f r o m 2 L

s l v a c a n t p l a c e t h r e e (03) a v a i l a b l e a l p h a b e t s

(A, B, H, L) s o p e r m u t a t i o n = 4 \times 3 \times 2 = 24

(e n d b y D s t a r t b y H + e n d b y D s t a r t b y o t h e r) = 24

3) w o r d s s t a r t b y H a n d e n d b y D

\underset{1}{H} \underset{2}{-} \underset{3}{-} \underset{4}{D}

o n e A f r o m 4 A

o n e B f r o m 1 B

o n e L f r o m 2 L

v a c a n t p l a c e t w o (02) a v a i l a b l e a l p h b e t s

(A, B, L) p e r m u t a t i o n 3 \times 2 = 6

(s t a r t H a n d e n d b y D) = 6

P o r Q = P \cup Q = P + Q - P \cap Q

P a n d Q = P \cap Q

s o r e s u l t s i s 24 + 24 - 6 = 42

Commented by tanmay.chaudhury50@gmail.com last updated on 07/Dec/18

t h a n k s \dots

Commented by Kunal12588 last updated on 07/Dec/18

l o v e d h o w y o u u s e d s e t s

Commented by rahul 19 last updated on 07/Dec/18

thank you sir! Finally, By Vienn diagram or , and becomes more clear!