Question Number 56205 by 121194 last updated on 12/Mar/19
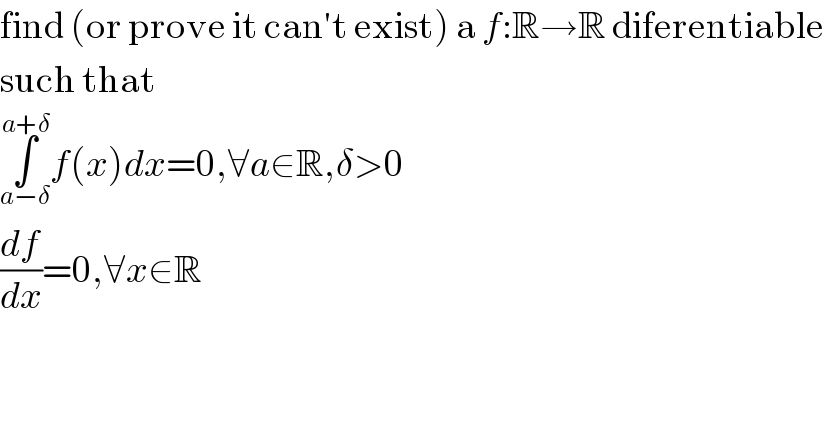
$$\mathrm{find}\:\left(\mathrm{or}\:\mathrm{prove}\:\mathrm{it}\:\mathrm{can}'\mathrm{t}\:\mathrm{exist}\right)\:\mathrm{a}\:{f}:\mathbb{R}\rightarrow\mathbb{R}\:\mathrm{diferentiable} \\ $$$$\mathrm{such}\:\mathrm{that} \\ $$$$\underset{{a}−\delta} {\overset{{a}+\delta} {\int}}{f}\left({x}\right){dx}=\mathrm{0},\forall{a}\in\mathbb{R},\delta>\mathrm{0} \\ $$$$\frac{{df}}{{dx}}=\mathrm{0},\forall{x}\in\mathbb{R} \\ $$
Answered by MJS last updated on 12/Mar/19

$${f}\left({x}\right)=\mathrm{0} \\ $$
