Question Number 14752 by Tinkutara last updated on 04/Jun/17
![Find ordered pair of (x, y) given x, y ∈ [0, 2π] if 3^(sin x + cos y) = 1 and 5^(sin^2 x + cos^2 y) = 5](https://www.tinkutara.com/question/Q14752.png)
$$\mathrm{Find}\:\mathrm{ordered}\:\mathrm{pair}\:\mathrm{of}\:\left({x},\:{y}\right)\:\mathrm{given}\:{x},\:{y}\:\in \\ $$$$\left[\mathrm{0},\:\mathrm{2}\pi\right]\:\mathrm{if}\:\mathrm{3}^{\mathrm{sin}\:{x}\:+\:\mathrm{cos}\:{y}} \:=\:\mathrm{1}\:\mathrm{and} \\ $$$$\mathrm{5}^{\mathrm{sin}^{\mathrm{2}} \:{x}\:+\:\mathrm{cos}^{\mathrm{2}} \:{y}} \:=\:\mathrm{5} \\ $$
Commented by Tinkutara last updated on 04/Jun/17

$$\mathrm{Answer}\:\mathrm{given}\:\mathrm{is}\:\mathrm{total}\:\mathrm{8}\:\mathrm{ordered}\:\mathrm{pairs} \\ $$$$\mathrm{and}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{such}\:\mathrm{pair}\:\mathrm{as}\:\mathrm{your} \\ $$$$\mathrm{answer}. \\ $$
Commented by 1kanika# last updated on 04/Jun/17
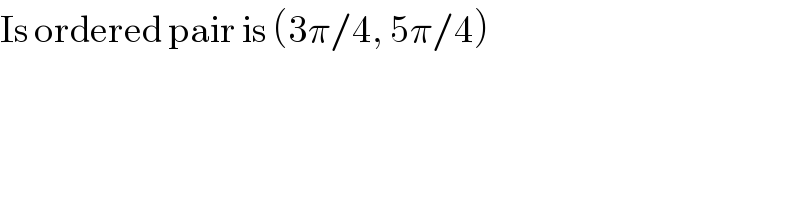
$$\mathrm{Is}\:\mathrm{ordered}\:\mathrm{pair}\:\mathrm{is}\:\left(\mathrm{3}\pi/\mathrm{4},\:\mathrm{5}\pi/\mathrm{4}\right) \\ $$
Commented by mrW1 last updated on 04/Jun/17
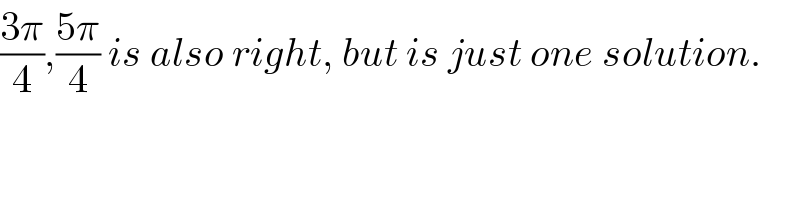
$$\frac{\mathrm{3}\pi}{\mathrm{4}},\frac{\mathrm{5}\pi}{\mathrm{4}}\:{is}\:{also}\:{right},\:{but}\:{is}\:{just}\:{one}\:{solution}. \\ $$
Commented by 1kanika# last updated on 04/Jun/17
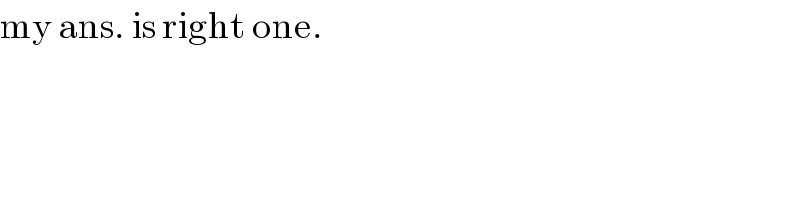
$$\mathrm{my}\:\mathrm{ans}.\:\mathrm{is}\:\mathrm{right}\:\mathrm{one}. \\ $$
Answered by mrW1 last updated on 04/Jun/17
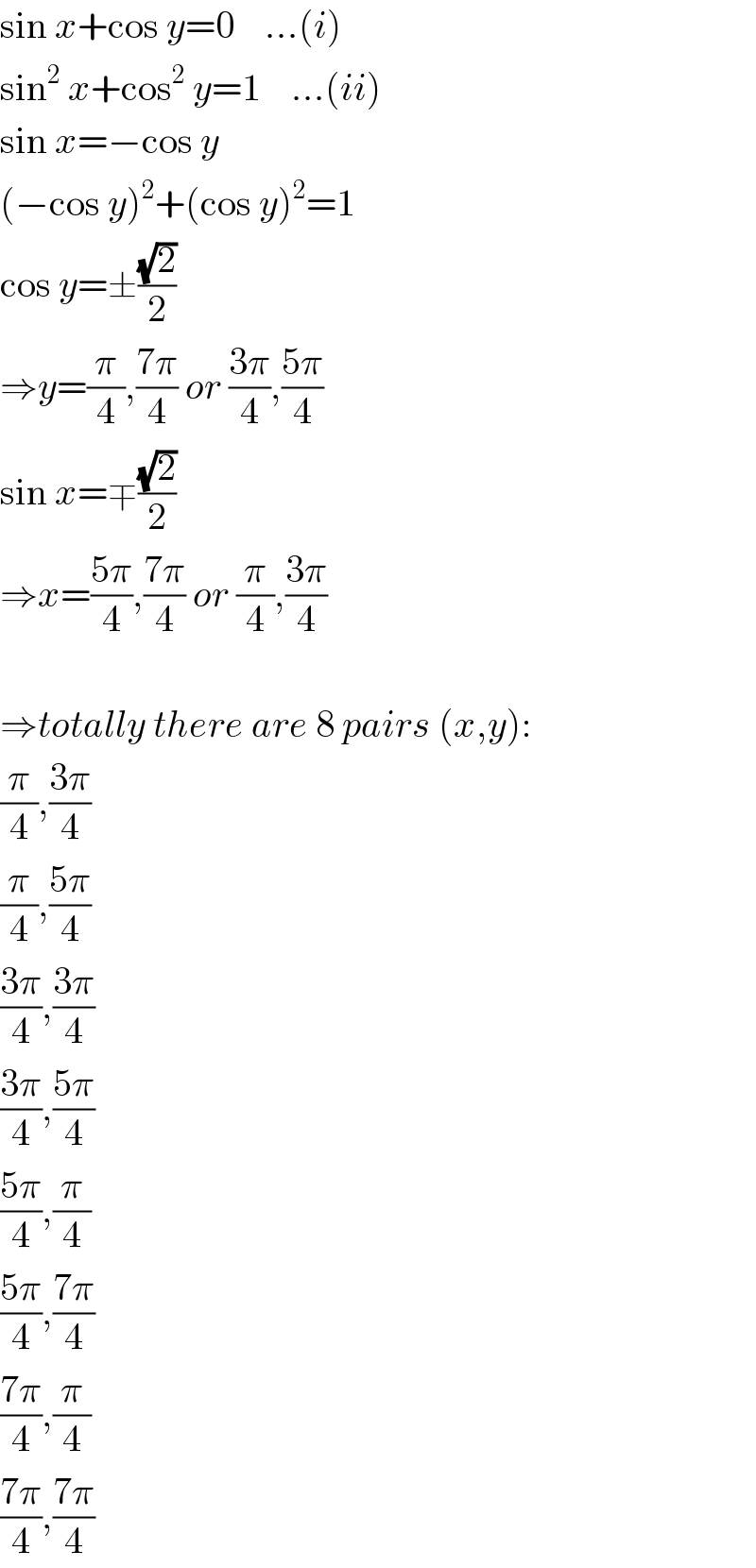
$$\mathrm{sin}\:{x}+\mathrm{cos}\:{y}=\mathrm{0}\:\:\:\:…\left({i}\right) \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{y}=\mathrm{1}\:\:\:\:…\left({ii}\right) \\ $$$$\mathrm{sin}\:{x}=−\mathrm{cos}\:{y} \\ $$$$\left(−\mathrm{cos}\:{y}\right)^{\mathrm{2}} +\left(\mathrm{cos}\:{y}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{cos}\:{y}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow{y}=\frac{\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}}\:{or}\:\frac{\mathrm{3}\pi}{\mathrm{4}},\frac{\mathrm{5}\pi}{\mathrm{4}} \\ $$$$\mathrm{sin}\:{x}=\mp\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}}\:{or}\:\frac{\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$ \\ $$$$\Rightarrow{totally}\:{there}\:{are}\:\mathrm{8}\:{pairs}\:\left({x},{y}\right): \\ $$$$\frac{\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$\frac{\pi}{\mathrm{4}},\frac{\mathrm{5}\pi}{\mathrm{4}} \\ $$$$\frac{\mathrm{3}\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$\frac{\mathrm{3}\pi}{\mathrm{4}},\frac{\mathrm{5}\pi}{\mathrm{4}} \\ $$$$\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\pi}{\mathrm{4}} \\ $$$$\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}} \\ $$$$\frac{\mathrm{7}\pi}{\mathrm{4}},\frac{\pi}{\mathrm{4}} \\ $$$$\frac{\mathrm{7}\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}} \\ $$
Commented by Tinkutara last updated on 04/Jun/17
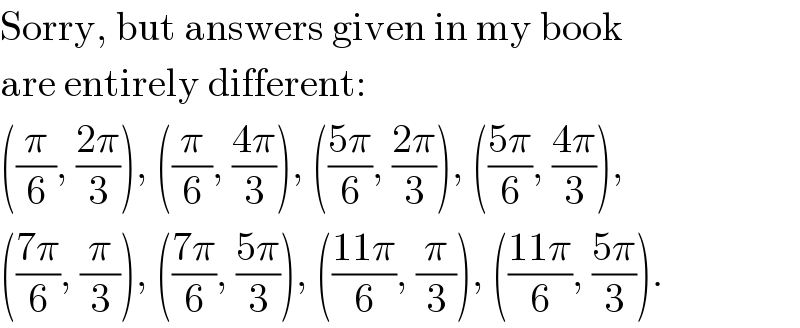
$$\mathrm{Sorry},\:\mathrm{but}\:\mathrm{answers}\:\mathrm{given}\:\mathrm{in}\:\mathrm{my}\:\mathrm{book} \\ $$$$\mathrm{are}\:\mathrm{entirely}\:\mathrm{different}: \\ $$$$\left(\frac{\pi}{\mathrm{6}},\:\frac{\mathrm{2}\pi}{\mathrm{3}}\right),\:\left(\frac{\pi}{\mathrm{6}},\:\frac{\mathrm{4}\pi}{\mathrm{3}}\right),\:\left(\frac{\mathrm{5}\pi}{\mathrm{6}},\:\frac{\mathrm{2}\pi}{\mathrm{3}}\right),\:\left(\frac{\mathrm{5}\pi}{\mathrm{6}},\:\frac{\mathrm{4}\pi}{\mathrm{3}}\right), \\ $$$$\left(\frac{\mathrm{7}\pi}{\mathrm{6}},\:\frac{\pi}{\mathrm{3}}\right),\:\left(\frac{\mathrm{7}\pi}{\mathrm{6}},\:\frac{\mathrm{5}\pi}{\mathrm{3}}\right),\:\left(\frac{\mathrm{11}\pi}{\mathrm{6}},\:\frac{\pi}{\mathrm{3}}\right),\:\left(\frac{\mathrm{11}\pi}{\mathrm{6}},\:\frac{\mathrm{5}\pi}{\mathrm{3}}\right). \\ $$
Commented by ajfour last updated on 04/Jun/17
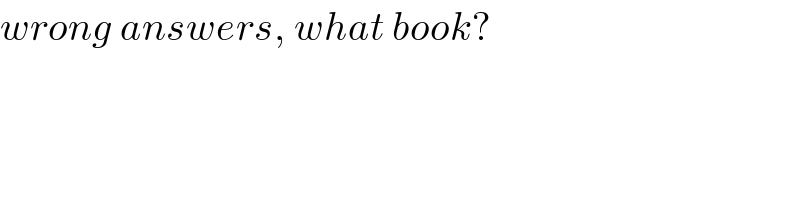
$${wrong}\:{answers},\:{what}\:{book}? \\ $$
Commented by Tinkutara last updated on 04/Jun/17

$$\mathrm{It}'\mathrm{s}\:\mathrm{my}\:\mathrm{coaching}\:\mathrm{institute}'\mathrm{s}\:\mathrm{book}\:\mathrm{for} \\ $$$$\mathrm{JEE}\:\mathrm{preparation}\:\mathrm{in}\:\mathrm{Class}\:\mathrm{XI}. \\ $$
Commented by mrW1 last updated on 04/Jun/17

$${That}\:{book}\:{is}\:{misleading}. \\ $$
