Question Number 33400 by rahul 19 last updated on 15/Apr/18
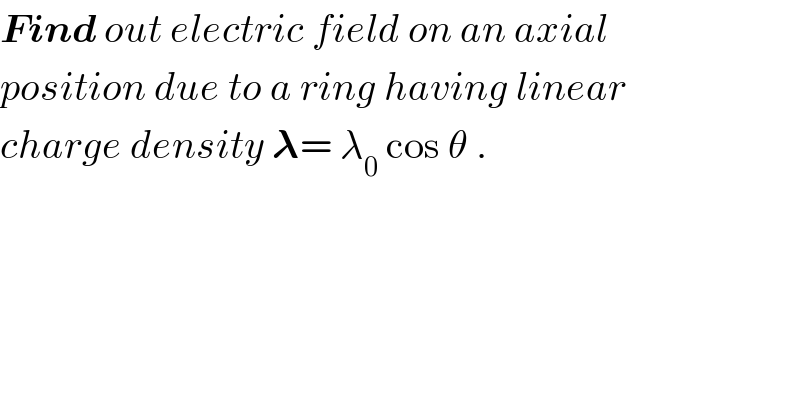
$$\boldsymbol{{Find}}\:{out}\:{electric}\:{field}\:{on}\:{an}\:{axial}\: \\ $$$${position}\:{due}\:{to}\:{a}\:{ring}\:{having}\:{linear} \\ $$$${charge}\:{density}\:\boldsymbol{\lambda}=\:\lambda_{\mathrm{0}} \:\mathrm{cos}\:\theta\:. \\ $$
Commented by ajfour last updated on 16/Apr/18
Commented by ajfour last updated on 16/Apr/18
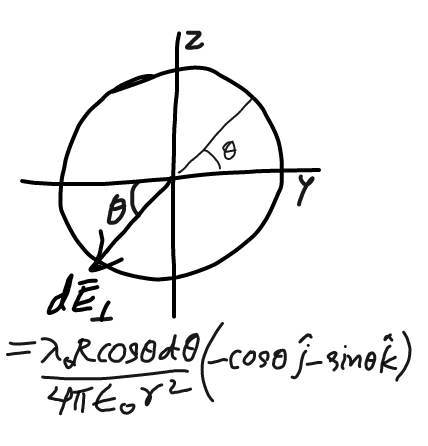
Commented by ajfour last updated on 16/Apr/18
![E_⊥ ^� =(dQ/(4πε_0 r^2 ))((R/r))(−cos θj^� −sin θk^� ) [in diagram above i forgot to include the ((R/r)) factor ] =((λ_0 R^2 cos θdθ)/(4πε_0 r^3 )) (−cos θj^� −sin θk^� ) E_x =0 , E_z =0 E_y =−((λ_0 R^2 )/(4πε_0 (x^2 +R^2 )^(3/2) )) ∫_0 ^( 2π) cos^2 θdθ =−((λ_0 R^2 )/(4πε_0 (x^2 +R^2 )^(3/2) ))×(1/2)∫_0 ^( 2π) (1+cos 2θ)dθ =−((λ_0 R^2 )/(4πε_0 (x^2 +R^2 )^(3/2) ))×(1/2)(2π) E = ∣E_y ∣=((𝛌_0 R^2 )/(4𝛆_0 (x^2 +R^2 )^(3/2) )) .](https://www.tinkutara.com/question/Q33439.png)
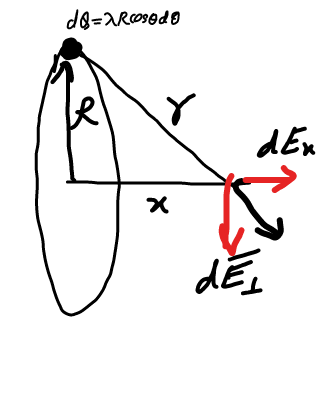
$$\bar {{E}}_{\bot} =\frac{{dQ}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {r}^{\mathrm{2}} }\left(\frac{{R}}{{r}}\right)\left(−\mathrm{cos}\:\theta\hat {{j}}−\mathrm{sin}\:\theta\hat {{k}}\right) \\ $$$$\left[{in}\:{diagram}\:{above}\:{i}\:{forgot}\:{to}\right. \\ $$$$\left.{include}\:{the}\:\:\:\left(\frac{{R}}{{r}}\right)\:\:{factor}\:\:\right] \\ $$$$\:\:\:\:\:=\frac{\lambda_{\mathrm{0}} {R}^{\mathrm{2}} \mathrm{cos}\:\theta{d}\theta}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {r}^{\mathrm{3}} }\:\left(−\mathrm{cos}\:\theta\hat {{j}}−\mathrm{sin}\:\theta\hat {{k}}\right) \\ $$$${E}_{{x}} =\mathrm{0}\:\:,\:\:{E}_{{z}} =\mathrm{0} \\ $$$${E}_{{y}} =−\frac{\lambda_{\mathrm{0}} {R}^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left({x}^{\mathrm{2}} +{R}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }\:\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} \mathrm{cos}\:^{\mathrm{2}} \theta{d}\theta \\ $$$$\:\:\:\:\:=−\frac{\lambda_{\mathrm{0}} {R}^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left({x}^{\mathrm{2}} +{R}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right){d}\theta \\ $$$$\:\:=−\frac{\lambda_{\mathrm{0}} {R}^{\mathrm{2}} }{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left({x}^{\mathrm{2}} +{R}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\pi\right) \\ $$$${E}\:=\:\mid{E}_{{y}} \mid=\frac{\boldsymbol{\lambda}_{\mathrm{0}} {R}^{\mathrm{2}} }{\mathrm{4}\boldsymbol{\epsilon}_{\mathrm{0}} \left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{R}}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }\:\:. \\ $$
Commented by rahul 19 last updated on 16/Apr/18

$${thank}\:{u}\:{sir}. \\ $$
