Question Number 117816 by snipers237 last updated on 13/Oct/20
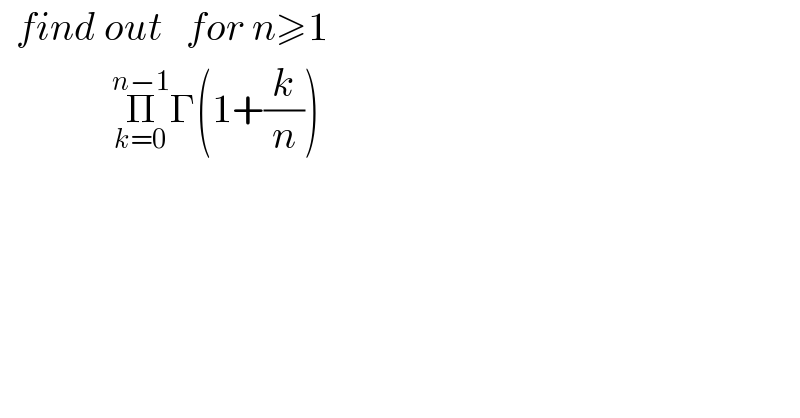
$$\:\:{find}\:{out}\:\:\:{for}\:{n}\geqslant\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\Gamma\left(\mathrm{1}+\frac{{k}}{{n}}\right) \\ $$$$ \\ $$
Answered by mnjuly1970 last updated on 14/Oct/20
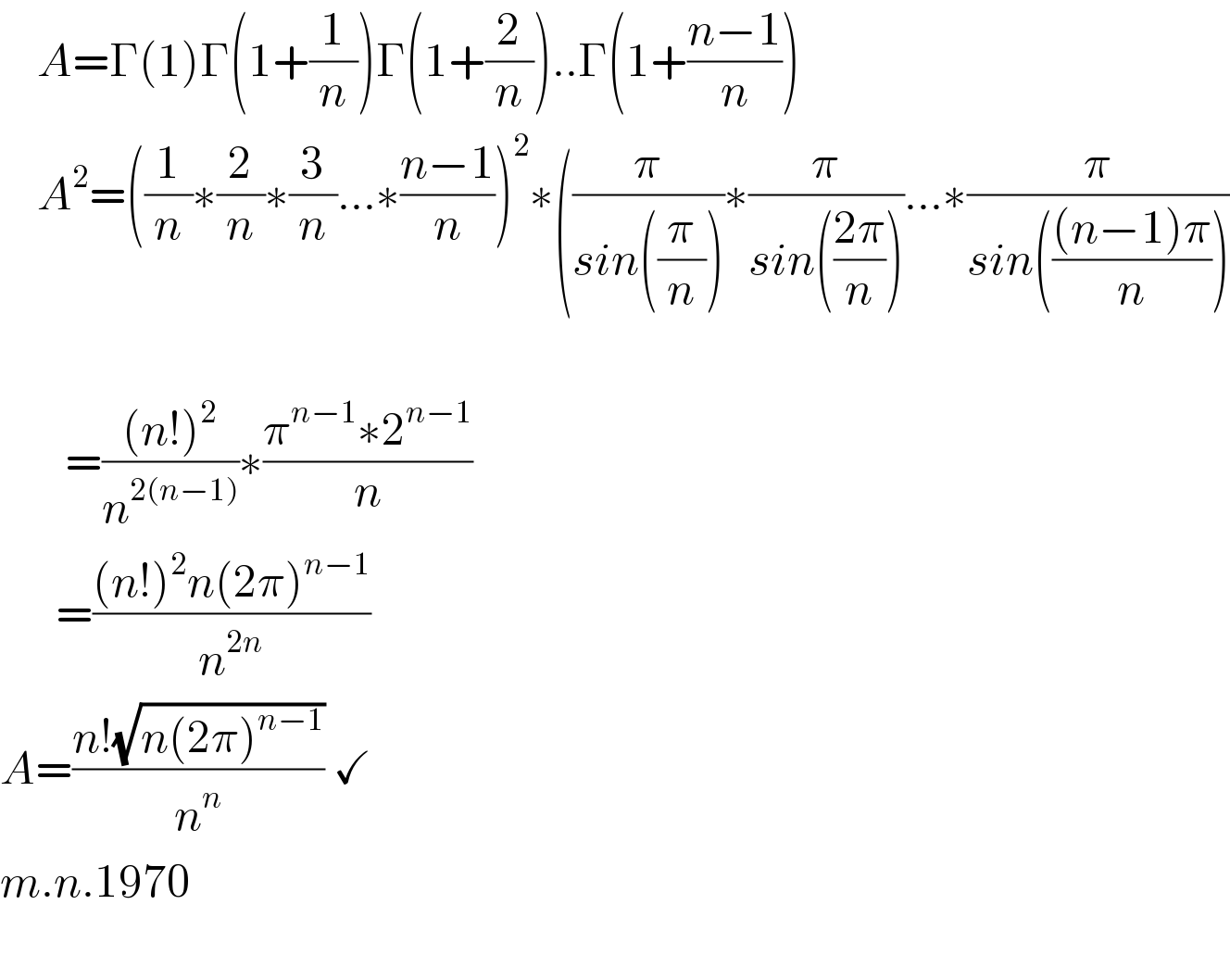
$$\:\:\:\:{A}=\Gamma\left(\mathrm{1}\right)\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\Gamma\left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right)..\Gamma\left(\mathrm{1}+\frac{{n}−\mathrm{1}}{{n}}\right) \\ $$$$\:\:\:\:{A}^{\mathrm{2}} =\left(\frac{\mathrm{1}}{{n}}\ast\frac{\mathrm{2}}{{n}}\ast\frac{\mathrm{3}}{{n}}…\ast\frac{{n}−\mathrm{1}}{{n}}\right)^{\mathrm{2}} \ast\left(\frac{\pi}{{sin}\left(\frac{\pi}{{n}}\right)}\ast\frac{\pi}{{sin}\left(\frac{\mathrm{2}\pi}{{n}}\right)}…\ast\frac{\pi}{{sin}\left(\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}\right)}\right. \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:=\frac{\left({n}!\right)^{\mathrm{2}} }{{n}^{\mathrm{2}\left({n}−\mathrm{1}\right)} }\ast\frac{\pi^{{n}−\mathrm{1}} \ast\mathrm{2}^{{n}−\mathrm{1}} }{{n}} \\ $$$$\:\:\:\:\:\:=\frac{\left({n}!\right)^{\mathrm{2}} {n}\left(\mathrm{2}\pi\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}{n}} }\: \\ $$$${A}=\frac{{n}!\sqrt{{n}\left(\mathrm{2}\pi\right)^{{n}−\mathrm{1}} }}{{n}^{{n}} }\:\checkmark \\ $$$${m}.{n}.\mathrm{1970} \\ $$$$\:\:\:\:\: \\ $$
