Menu Close

Find-out-some-pairs-a-b-such-that-for-some-n-1-a-n-b-n-a-2n-b-2n-a-4n-b-4n-a-8n-b-8n-P-

Tinku Tara 0 Comments
Pin




Question Number 160061 by Rasheed.Sindhi last updated on 24/Nov/21
Find out some pairs (a,b) such that for some n≥1 a^n +b^n ,a^(2n) +b^(2n) ,a^(4n) +b^(4n) ,a^(8n) +b^(8n) ∈P
$$ \\ $$$${Find}\:{out}\:{some}\:{pairs}\:\left({a},{b}\right)\:{such}\:{that} \\ $$$${for}\:{some}\:{n}\geqslant\mathrm{1} \\ $$$${a}^{{n}} +{b}^{{n}} ,{a}^{\mathrm{2}{n}} +{b}^{\mathrm{2}{n}} ,{a}^{\mathrm{4}{n}} +{b}^{\mathrm{4}{n}} ,{a}^{\mathrm{8}{n}} +{b}^{\mathrm{8}{n}} \in\mathbb{P} \\ $$$$ \\ $$
Answered by nikif99 last updated on 24/Nov/21
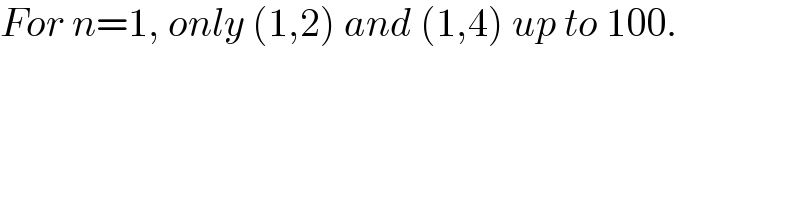
For n=1, only (1,2) and (1,4) up to 100.
$${For}\:{n}=\mathrm{1},\:{only}\:\left(\mathrm{1},\mathrm{2}\right)\:{and}\:\left(\mathrm{1},\mathrm{4}\right)\:{up}\:{to}\:\mathrm{100}. \\ $$
Commented by Rasheed.Sindhi last updated on 24/Nov/21
ThanX a lot sir! Your first example is an example of 5-level 1+2=3∈P 1^2 +2^2 =5∈P 1^4 +2^4 =17∈P 1^8 +2^8 =257∈P 1^(16) +2^(16) =65537∈P I′ve also searched but my search was not very systematic and I ignored small numbers like 1 & 2,so be not successful!Anyway now we can say that maximum number of levels≥5 THANKS again for your labour and attention sir! BTW, did you use a program for searching such numbers?
$$\mathcal{T}{han}\mathcal{X}\:{a}\:{lot}\:{sir}!\:{Your}\:{first}\:{example} \\ $$$${is}\:{an}\:{example}\:{of}\:\mathrm{5}-{level}\: \\ $$$$\mathrm{1}+\mathrm{2}=\mathrm{3}\in\mathbb{P} \\ $$$$\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} =\mathrm{5}\in\mathbb{P} \\ $$$$\mathrm{1}^{\mathrm{4}} +\mathrm{2}^{\mathrm{4}} =\mathrm{17}\in\mathbb{P} \\ $$$$\mathrm{1}^{\mathrm{8}} +\mathrm{2}^{\mathrm{8}} =\mathrm{257}\in\mathbb{P} \\ $$$$\mathrm{1}^{\mathrm{16}} +\mathrm{2}^{\mathrm{16}} =\mathrm{65537}\in\mathbb{P} \\ $$$${I}'{ve}\:{also}\:{searched}\:{but}\:{my}\:{search} \\ $$$${was}\:{not}\:{very}\:{systematic}\:{and}\:{I}\:{ignored} \\ $$$${small}\:{numbers}\:{like}\:\mathrm{1}\:\&\:\mathrm{2},{so}\:{be}\:{not} \\ $$$${successful}!{Anyway}\:{now}\:{we}\:{can}\:{say}\:{that} \\ $$$${maximum}\:{number}\:{of}\:{levels}\geqslant\mathrm{5} \\ $$$$\mathbb{THANKS}\:\mathrm{again}\:\mathrm{for}\:\mathrm{your}\:\mathrm{labour} \\ $$$$\mathrm{and}\:\mathrm{attention}\:\boldsymbol{\mathrm{sir}}! \\ $$$$\mathcal{BTW},\:{did}\:{you}\:{use}\:{a}\:{program}\:{for}\: \\ $$$${searching}\:{such}\:{numbers}? \\ $$
Commented by Rasheed.Sindhi last updated on 24/Nov/21
BTW sir, you seemed an expdrienced member of the forum.Are you really an old member of the forum?
$$\mathcal{BTW}\:{sir},\:{you}\:{seemed}\:{an}\:{expdrienced} \\ $$$${member}\:{of}\:{the}\:{forum}.{Are}\:{you}\:{really} \\ $$$${an}\:{old}\:{member}\:{of}\:{the}\:{forum}? \\ $$
Commented by Rasheed.Sindhi last updated on 24/Nov/21
Thanks nikif sir, very much!
$$\mathcal{T}{hanks}\:{nikif}\:{sir},\:{very}\:{much}! \\ $$
Commented by nikif99 last updated on 24/Nov/21
Programming in Pascal (dinosaure as programming language). Although useful in computing 8th power. I recently joined this group. I am a hobbist of math.
$${Programming}\:{in}\:{Pascal}\:\left({dinosaure}\:{as}\right. \\ $$$$\left.{programming}\:{language}\right).\:{Although} \\ $$$${useful}\:{in}\:{computing}\:\mathrm{8}{th}\:{power}. \\ $$$${I}\:{recently}\:{joined}\:{this}\:{group}.\:{I}\:{am}\:{a} \\ $$$${hobbist}\:{of}\:{math}. \\ $$
Commented by Rasheed.Sindhi last updated on 25/Nov/21
A trivial example of infinity-level is pair is(1,1).Because 1^n +1^n =2∈P ∀n∈N
$${A}\:{trivial}\:{example}\:{of}\:{infinity}-{level} \\ $$$${is}\:{pair}\:{is}\left(\mathrm{1},\mathrm{1}\right).{Because}\:\mathrm{1}^{{n}} +\mathrm{1}^{{n}} =\mathrm{2}\in\mathbb{P} \\ $$$$\forall{n}\in\mathbb{N} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *