Question Number 62214 by Rasheed.Sindhi last updated on 17/Jun/19
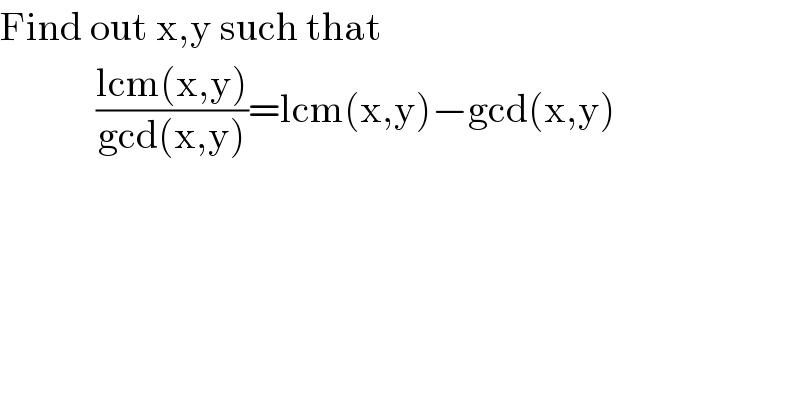
$$\mathrm{Find}\:\mathrm{out}\:\mathrm{x},\mathrm{y}\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{lcm}\left(\mathrm{x},\mathrm{y}\right)}{\mathrm{gcd}\left(\mathrm{x},\mathrm{y}\right)}=\mathrm{lcm}\left(\mathrm{x},\mathrm{y}\right)−\mathrm{gcd}\left(\mathrm{x},\mathrm{y}\right) \\ $$
Answered by MJS last updated on 17/Jun/19
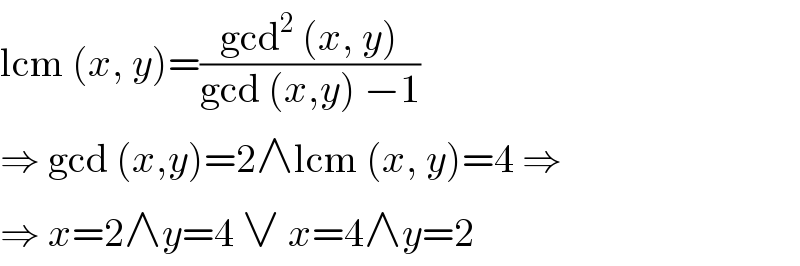
$$\mathrm{lcm}\:\left({x},\:{y}\right)=\frac{\mathrm{gcd}^{\mathrm{2}} \:\left({x},\:{y}\right)}{\mathrm{gcd}\:\left({x},{y}\right)\:−\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{gcd}\:\left({x},{y}\right)=\mathrm{2}\wedge\mathrm{lcm}\:\left({x},\:{y}\right)=\mathrm{4}\:\Rightarrow\: \\ $$$$\Rightarrow\:{x}=\mathrm{2}\wedge{y}=\mathrm{4}\:\vee\:{x}=\mathrm{4}\wedge{y}=\mathrm{2} \\ $$
Commented by Rasheed.Sindhi last updated on 18/Jun/19

$$\mathcal{TH}\alpha{nk}\:{you}\:\mathcal{S}{ir}! \\ $$
