Find-p-and-q-such-that-p-2-q-2-101-2-Where-p-q-Z-different-from-zero-

Question Number 113689 by Ar Brandon last updated on 14/Sep/20

Find p and q such that

p^{2} + q^{2} = 101^{2} . Where p, q \in Z

different from zero .

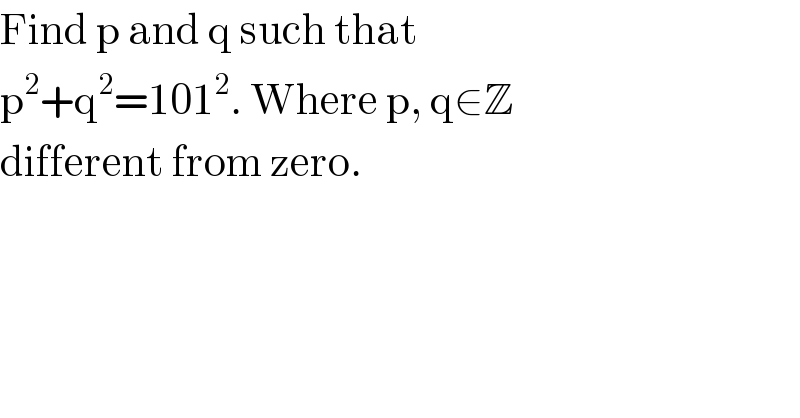
Commented by Rasheed.Sindhi last updated on 14/Sep/20

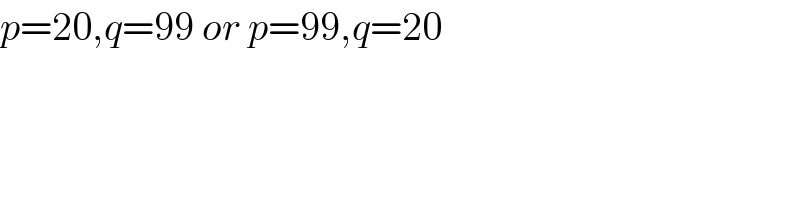
p = 20, q = 99 o r p = 99, q = 20

Answered by nimnim last updated on 14/Sep/20

If a, b and c are primitive pythagorean triples

then : -

Case (1) when a = odd,

b = \frac{a^{2}}{2} - \frac{1}{2} and c = \frac{a^{2}}{2} + \frac{1}{2}

Let a = 13, c = \frac{169}{2} + \frac{1}{2} = 85 \neq 101

a = 15, c = \frac{225}{2} + \frac{1}{2} = 113 \neq 101

Case (2) when a = even

b = {(\frac{a}{2})}^{2} - 1 and c = {(\frac{a}{2})}^{2} + 1

Let a = 20, c = {(\frac{20}{2})}^{2} + 1 = 101

b = {(\frac{20}{2})}^{2} - 1 = 99

\Rightarrow (p, q) = (20, 99) or (99, 20)

Answered by Rasheed.Sindhi last updated on 15/Sep/20

I f m & n a r e \boldsymbol a n y p o s i t i v e

i n t e g e r s w i t h m > n

(m^{2} - n^{2}, 2 m n, m^{2} + n^{2}) i s a

p a t h a g o r e a n t r i p l e t .

T h i s r u l e i s p e r f e c t, i t c a n p r o d u c e

\boldsymbol a l l t h e p a t h a g o r e a n t r i p l e t s a n d

t h a t a l s o m e a n s t h a t f o r \boldsymbol e v e r y

t r i p l e t t h e r e e x i s t m & n w h i c h

c a n p r o d u c e t h a t t r i p l e t .

H e r e (p, q, 101) i s p a t h a g o r e a n

t r i p l e t s o m^{2} + n^{2} = 101

o r m^{2} = 101 - n^{2} . C l e a r l y

n ⩽ ⌊ \sqrt{101} ⌋, s o {w e}^{'} v e t o f i n d s u c h

n f o r w h i c h 101 - n^{2} i s p e r f e c t

s q u a r e b e t w e e n 1 a n d 10 .

H e n c e n = 1, 10 a r e o n l y p r o p e r

v a l u e s a n d c o r r e s p o n d i n g v a l u e s

o f m a r e 10, 1 . S i n c e m > n s o

(m, n) = (10, 1)

p = m^{2} - n^{2} = 10^{2} - 1^{2} = 99

q = 2 m n = 2 (10) (1) = 20

O r

p = 2 m n = 20

q = m^{2} - n^{2} = 99

S i n c e p, q \in Z

(p, q) = (20, 99), (20, - 99),

(- 20, 99), (- 20, - 99),

(99, 20), (99, - 20),

(- 99, 20), (- 99, - 20) .

Answered by 1549442205PVT last updated on 16/Sep/20

We known that (a, b, c) is a triple of

Pythagor posirive integer numbers

where b^{2} + c^{2} = a^{2}

(a, b) = 1 if and only if c = uv, b = \frac{u^{2} - v^{2}}{2},

a = \frac{u^{2} + v^{2}}{2} where u, v are odd and coprime

. In the our problem p^{2} + q^{2} = 101^{2} (*)

Since 101 is a prime, so (p, q) = 1 .

Hence, p = uv, q = \frac{u^{2} - v^{2}}{2}, \frac{u^{2} + v^{2}}{2} = 101

\Leftrightarrow u^{2} + v^{2} = 202 \Rightarrow v < 9 < u ⩽ 13

i) If u = 13 then v^{2} = 202 - 169 = 33 \Rightarrow rejected

ii) If u = 11 then v^{2} = 202 - 121 = 81 = 9^{2}

\Rightarrow v = 9 \Rightarrow p = uv = 99, q = \frac{11^{2} - 9^{2}}{2} = 20

Since p, q have equal role in the

equation, we obtain

(\boldsymbol p, \boldsymbol q) \in {(99, 20), (20, 99) . From this

follows (- p, q), (p, - q), (- p, - q)

also satisfying

\boldsymbol second \boldsymbol way :

If (p, q) is a root of (*) then (- p, q), (p, - q)

and (- p, - q) are also roots of (*) . Hence

we just need find pairs (p, q) of positive

integer numbers of the equation (*)

Since 101 is a prime number, p and q

are coprime (because suppose that

\gcd (p, q) = d \neq 1 then p = md, q = nd with

(m, n) = 1 . Then p^{2} + q^{2} = 101^{2} (*)

\Leftrightarrow (m^{2} + n^{2}) d^{2} = 101^{2} \Rightarrow 101 ⋮ d which is

contradiction to the fact that 101 is prime)

. Furthermore, among two numbers p, q

must have one number is even and other

number is odd . Hence, WLOG suppose

p is odd and q is even . From that we have

(*) \Leftrightarrow p^{2} = (101 + q) (101 - q)

Put 101 + q = m, 101 - q = n \Rightarrow m > n, we

get p^{2} = mn, q = \frac{m - n}{2}, 101 = \frac{m + n}{2} .

We see that m and n - coprime .

because of suppose the contrary, that

\gcd (m, n) = d \neq 1 . Then m = m_{1} d, n = n_{1} d

From that 101 = \frac{m + n}{2} = \frac{m_{1} + n_{1}}{2} d

which is impossible since 101 is prime

Therefore, m and n are coprime . From

p^{2} = mn and (m, n) = 1 we infer

m = u^{2}, n = v^{2} where u and v - coprime,

u > v > 0 and are odd numbers . Finally,

we obtain {\begin{cases} p = uv (1) \\ q = \frac{u^{2} - v^{2}}{2} (2) \\ 101 = \frac{u^{2} + v^{2}}{2} (3) \end{cases}

(3) \Leftrightarrow u^{2} + v^{2} = 202 \Rightarrow v < 11 ⩽ u ⩽ 13

i) For u = 13 \Rightarrow v^{2} = 202 - 169 = 33 \Rightarrow ∄ v \in Z

ii) For u = 11 \Rightarrow v^{2} = 202 - 121 = 81

\Rightarrow v = 9 . Put into (1) (2) we get

(p, q) \in (99, 20) and due to above note and the

equality of p and q in equation we get

(p, q) \in {99, 20), (- 99, 20), (20, 99), (20, - 99),

(99, - 20), (- 99, - 20), (- 20, 99), (- 20, - 99)}