Question Number 182369 by mathocean1 last updated on 08/Dec/22
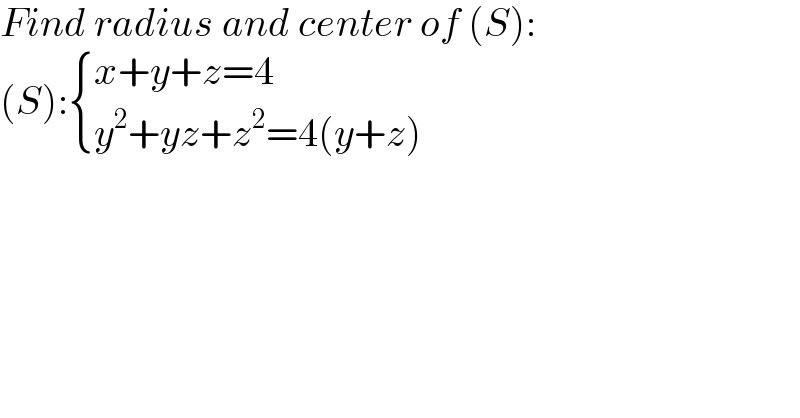
$${Find}\:{radius}\:{and}\:{center}\:{of}\:\left({S}\right): \\ $$$$\left({S}\right):\begin{cases}{{x}+{y}+{z}=\mathrm{4}}\\{{y}^{\mathrm{2}} +{yz}+{z}^{\mathrm{2}} =\mathrm{4}\left({y}+{z}\right)}\end{cases} \\ $$
Commented by a.lgnaoui last updated on 09/Dec/22
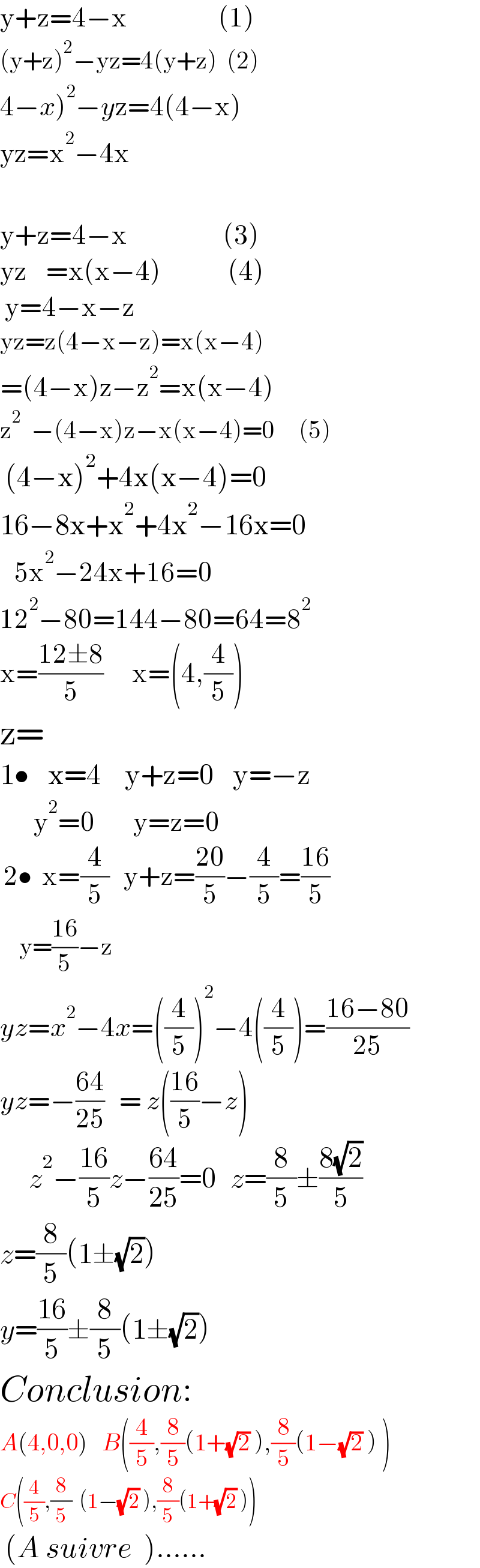
$$\mathrm{y}+\mathrm{z}=\mathrm{4}−\mathrm{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{y}+\mathrm{z}\right)^{\mathrm{2}} −\mathrm{yz}=\mathrm{4}\left(\mathrm{y}+\mathrm{z}\right)\:\:\left(\mathrm{2}\right) \\ $$$$\left.\mathrm{4}−{x}\right)^{\mathrm{2}} −{y}\mathrm{z}=\mathrm{4}\left(\mathrm{4}−\mathrm{x}\right) \\ $$$$\mathrm{yz}=\mathrm{x}^{\mathrm{2}} −\mathrm{4x} \\ $$$$ \\ $$$$\mathrm{y}+\mathrm{z}=\mathrm{4}−\mathrm{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$$\mathrm{yz}\:\:\:\:=\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{4}\right) \\ $$$$\:\mathrm{y}=\mathrm{4}−\mathrm{x}−\mathrm{z} \\ $$$$\mathrm{yz}=\mathrm{z}\left(\mathrm{4}−\mathrm{x}−\mathrm{z}\right)=\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right) \\ $$$$=\left(\mathrm{4}−\mathrm{x}\right)\mathrm{z}−\mathrm{z}^{\mathrm{2}} =\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right) \\ $$$$\mathrm{z}^{\mathrm{2}} \:\:−\left(\mathrm{4}−\mathrm{x}\right)\mathrm{z}−\mathrm{x}\left(\mathrm{x}−\mathrm{4}\right)=\mathrm{0}\:\:\:\:\:\left(\mathrm{5}\right)\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\left(\mathrm{4}−\mathrm{x}\right)^{\mathrm{2}} +\mathrm{4x}\left(\mathrm{x}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{16}−\mathrm{8x}+\mathrm{x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{2}} −\mathrm{16x}=\mathrm{0} \\ $$$$\:\:\:\mathrm{5x}^{\mathrm{2}} −\mathrm{24x}+\mathrm{16}=\mathrm{0} \\ $$$$\mathrm{12}^{\mathrm{2}} −\mathrm{80}=\mathrm{144}−\mathrm{80}=\mathrm{64}=\mathrm{8}^{\mathrm{2}} \\ $$$$\mathrm{x}=\frac{\mathrm{12}\pm\mathrm{8}}{\mathrm{5}}\:\:\:\:\:\:\mathrm{x}=\left(\mathrm{4},\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$$\mathrm{z}= \\ $$$$\mathrm{1}\bullet\:\:\:\:\mathrm{x}=\mathrm{4}\:\:\:\:\:\mathrm{y}+\mathrm{z}=\mathrm{0}\:\:\:\:\mathrm{y}=−\mathrm{z}\:\:\: \\ $$$$\:\:\:\:\:\:\:\mathrm{y}^{\mathrm{2}} =\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{y}=\mathrm{z}=\mathrm{0} \\ $$$$\:\mathrm{2}\bullet\:\:\mathrm{x}=\frac{\mathrm{4}}{\mathrm{5}}\:\:\:\mathrm{y}+\mathrm{z}=\frac{\mathrm{20}}{\mathrm{5}}−\frac{\mathrm{4}}{\mathrm{5}}=\frac{\mathrm{16}}{\mathrm{5}} \\ $$$$\:\:\:\:\mathrm{y}=\frac{\mathrm{16}}{\mathrm{5}}−\mathrm{z}\:\:\:\: \\ $$$${yz}={x}^{\mathrm{2}} −\mathrm{4}{x}=\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{2}} −\mathrm{4}\left(\frac{\mathrm{4}}{\mathrm{5}}\right)=\frac{\mathrm{16}−\mathrm{80}}{\mathrm{25}} \\ $$$${yz}=−\frac{\mathrm{64}}{\mathrm{25}}\:\:\:=\:{z}\left(\frac{\mathrm{16}}{\mathrm{5}}−{z}\right) \\ $$$$\:\:\:\:\:\:{z}^{\mathrm{2}} −\frac{\mathrm{16}}{\mathrm{5}}{z}−\frac{\mathrm{64}}{\mathrm{25}}=\mathrm{0}\:\:\:{z}=\frac{\mathrm{8}}{\mathrm{5}}\pm\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{5}} \\ $$$${z}=\frac{\mathrm{8}}{\mathrm{5}}\left(\mathrm{1}\pm\sqrt{\mathrm{2}}\right) \\ $$$${y}=\frac{\mathrm{16}}{\mathrm{5}}\pm\frac{\mathrm{8}}{\mathrm{5}}\left(\mathrm{1}\pm\sqrt{\mathrm{2}}\right) \\ $$$${Conclusion}: \\ $$$${A}\left(\mathrm{4},\mathrm{0},\mathrm{0}\right)\:\:\:{B}\left(\frac{\mathrm{4}}{\mathrm{5}},\frac{\mathrm{8}}{\mathrm{5}}\left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right),\frac{\mathrm{8}}{\mathrm{5}}\left(\mathrm{1}−\sqrt{\mathrm{2}}\:\right)\:\right) \\ $$$${C}\left(\frac{\mathrm{4}}{\mathrm{5}},\frac{\mathrm{8}}{\mathrm{5}}\:\:\left(\mathrm{1}−\sqrt{\mathrm{2}}\:\right),\frac{\mathrm{8}}{\mathrm{5}}\left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right)\right) \\ $$$$\:\left({A}\:{suivre}\:\:\right)…… \\ $$
Commented by a.lgnaoui last updated on 09/Dec/22

Answered by mr W last updated on 10/Dec/22

$${the}\:{section}\:\left({S}\right)\:{of}\:{both}\:{surfaces}\:{is}\: \\ $$$${a}\:{circle}\:{with} \\ $$$${center}\:{at}\:\left(\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$${and}\:{radius}\:\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 10/Dec/22

$${sorry},\:{i}\:{checked}\:{again}.\:{the}\:{section}\:{is} \\ $$$${indeed}\:{a}\:{circle}.\:{i}\:{have}\:{fixed}\:{my}\:{answer}. \\ $$
Commented by a.lgnaoui last updated on 10/Dec/22

$${thank}\:{you}\: \\ $$
Commented by mr W last updated on 10/Dec/22

