Question Number 83653 by jagoll last updated on 05/Mar/20

$$\mathrm{find}\:\mathrm{range}\:\mathrm{of}\:\mathrm{function}\: \\ $$$$\mathrm{y}=\:\frac{\mathrm{4}}{\left({x}^{\mathrm{2}} −\mathrm{4}\right)} \\ $$
Answered by MJS last updated on 05/Mar/20

$${x}=\pm\mathrm{2}\sqrt{\frac{{y}+\mathrm{1}}{{y}}} \\ $$$$\Rightarrow\:{y}\leqslant−\mathrm{1}\vee{y}>\mathrm{0} \\ $$
Commented by jagoll last updated on 05/Mar/20

$$\mathrm{yess} \\ $$
Answered by jagoll last updated on 05/Mar/20
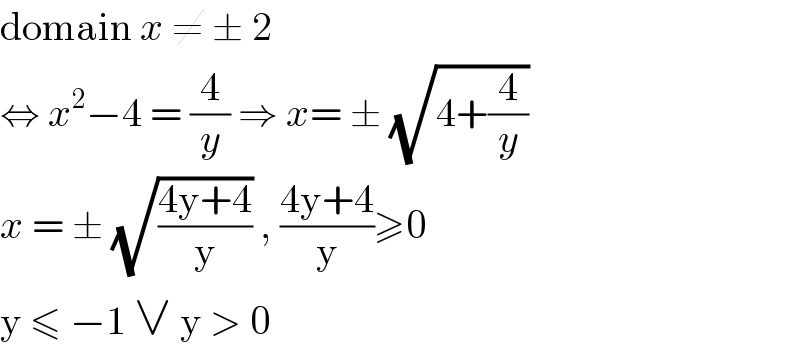
$$\mathrm{domain}\:{x}\:\neq\:\pm\:\mathrm{2} \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} −\mathrm{4}\:=\:\frac{\mathrm{4}}{{y}}\:\Rightarrow\:{x}=\:\pm\:\sqrt{\mathrm{4}+\frac{\mathrm{4}}{{y}}} \\ $$$${x}\:=\:\pm\:\sqrt{\frac{\mathrm{4y}+\mathrm{4}}{\mathrm{y}}}\:,\:\frac{\mathrm{4y}+\mathrm{4}}{\mathrm{y}}\geqslant\mathrm{0} \\ $$$$\mathrm{y}\:\leqslant\:−\mathrm{1}\:\vee\:\mathrm{y}\:>\:\mathrm{0} \\ $$
