Question Number 153257 by naka3546 last updated on 06/Sep/21
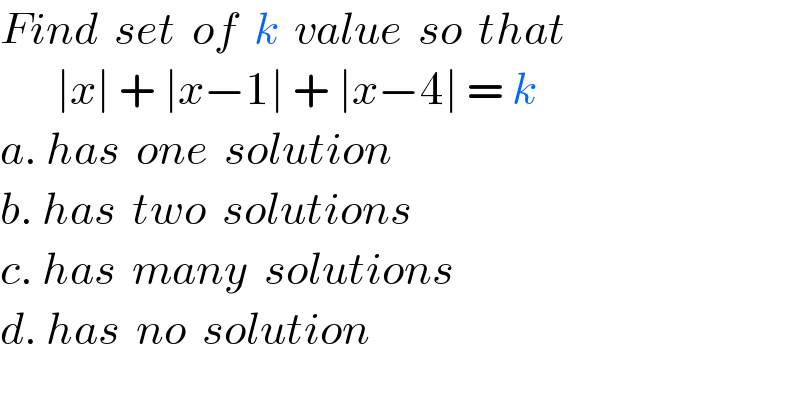
$${Find}\:\:{set}\:\:{of}\:\:{k}\:\:{value}\:\:{so}\:\:{that} \\ $$$$\:\:\:\:\:\:\:\mid{x}\mid\:+\:\mid{x}−\mathrm{1}\mid\:+\:\mid{x}−\mathrm{4}\mid\:=\:{k} \\ $$$${a}.\:{has}\:\:{one}\:\:{solution} \\ $$$${b}.\:{has}\:\:{two}\:\:{solutions} \\ $$$${c}.\:{has}\:\:{many}\:\:{solutions} \\ $$$${d}.\:{has}\:\:{no}\:\:{solution} \\ $$
Answered by ajfour last updated on 06/Sep/21

$${let}\:\:{x}−\mathrm{2}={t}\:,\:{then} \\ $$$$\mid{x}\mid+\mid{x}−\mathrm{1}\mid+\mid{x}−\mathrm{3}\mid+\mid{x}−\mathrm{4}\mid \\ $$$$\:\:\:={k}+\mid{x}−\mathrm{3}\mid \\ $$$$\Rightarrow\:\:\mid{t}+\mathrm{2}\mid+\mid{t}+\mathrm{1}\mid+\mid{t}−\mathrm{1}\mid+\mid{t}−\mathrm{2}\mid \\ $$$$\:\:\:={k}+\mid{t}−\mathrm{1}\mid \\ $$$${now}\:{we}\:{better}\:{use}\:{graph}: \\ $$$$\:\:\:{blue}\:{graph}\:=\:{red}\:{graph} \\ $$$${so}\:{for}\:{no}\:{solution}\:{k}<\mathrm{4} \\ $$$${one}\:{solution}\:\:\:\:{k}=\mathrm{4} \\ $$$${for}\:{three}\:{solutions},\left({two}\:{equal}\right) \\ $$$$\:\:\:\:\:\:{k}=\mathrm{6} \\ $$$${two}\:{solutions}\:\:\:{k}>\mathrm{4} \\ $$$${For}\:\:{more}\:{than}\:{two}\:\left({distinct}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{no}\:{real}\:{value}\:{of}\:{k}. \\ $$$$ \\ $$
Commented by ajfour last updated on 06/Sep/21

Answered by MJS_new last updated on 06/Sep/21
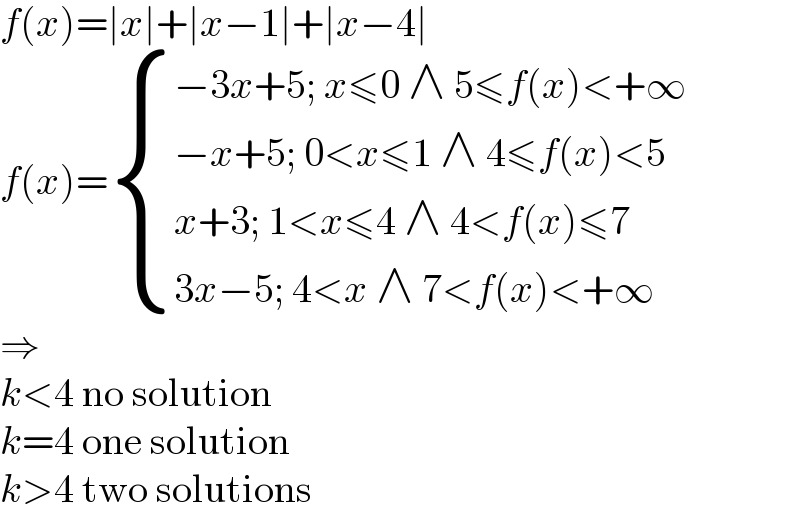
$${f}\left({x}\right)=\mid{x}\mid+\mid{x}−\mathrm{1}\mid+\mid{x}−\mathrm{4}\mid \\ $$$${f}\left({x}\right)=\begin{cases}{−\mathrm{3}{x}+\mathrm{5};\:{x}\leqslant\mathrm{0}\:\wedge\:\mathrm{5}\leqslant{f}\left({x}\right)<+\infty}\\{−{x}+\mathrm{5};\:\mathrm{0}<{x}\leqslant\mathrm{1}\:\wedge\:\mathrm{4}\leqslant{f}\left({x}\right)<\mathrm{5}\:}\\{{x}+\mathrm{3};\:\mathrm{1}<{x}\leqslant\mathrm{4}\:\wedge\:\mathrm{4}<{f}\left({x}\right)\leqslant\mathrm{7}}\\{\mathrm{3}{x}−\mathrm{5};\:\mathrm{4}<{x}\:\wedge\:\mathrm{7}<{f}\left({x}\right)<+\infty}\end{cases} \\ $$$$\Rightarrow \\ $$$${k}<\mathrm{4}\:\mathrm{no}\:\mathrm{solution} \\ $$$${k}=\mathrm{4}\:\mathrm{one}\:\mathrm{solution} \\ $$$${k}>\mathrm{4}\:\mathrm{two}\:\mathrm{solutions} \\ $$
