Find-shortest-distance-from-origin-to-the-cubic-y-x-3-10x-2-27x-18-

Question Number 54983 by ajfour last updated on 15/Feb/19

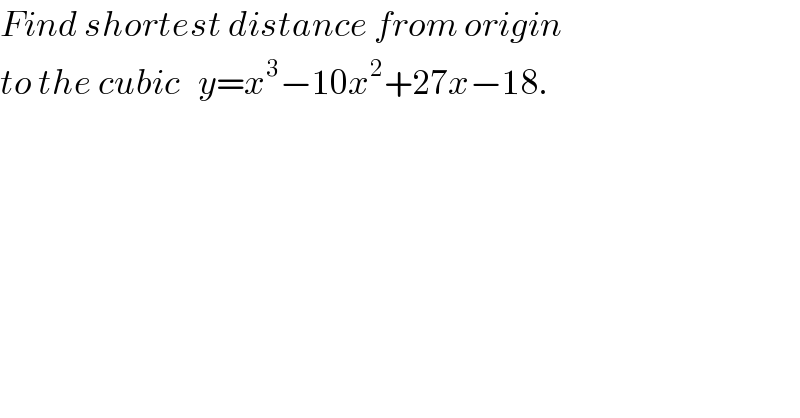
$${Find}\:{shortest}\:{distance}\:{from}\:{origin} \\ $$$${to}\:{the}\:{cubic}\:\:\:{y}={x}^{\mathrm{3}} −\mathrm{10}{x}^{\mathrm{2}} +\mathrm{27}{x}−\mathrm{18}. \\ $$

Commented by mr W last updated on 15/Feb/19

$${you}\:{can}\:{apply}\:{your}\:{solution}\:{method}\:{for} \\ $$$${quintic}\:{equations}\:{to}\:{solve}\:{this}\:{question}.\: \\ $$

Commented by ajfour last updated on 15/Feb/19

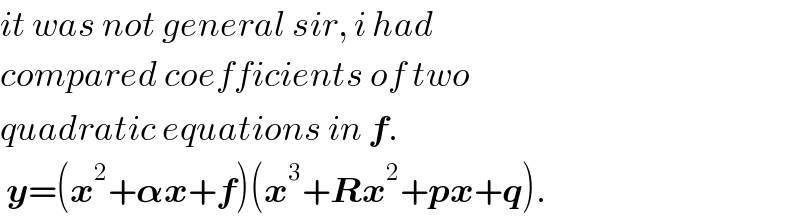
it was not general sir, i had compared coefficients of two quadratic equations in f. y=(x^2 +𝛂x+f)(x^3 +Rx^2 +px+q).

$${it}\:{was}\:{not}\:{general}\:{sir},\:{i}\:{had} \\ $$$${compared}\:{coefficients}\:{of}\:{two} \\ $$$${quadratic}\:{equations}\:{in}\:\boldsymbol{{f}}. \\ $$$$\:\boldsymbol{{y}}=\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{\alpha{x}}+\boldsymbol{{f}}\right)\left(\boldsymbol{{x}}^{\mathrm{3}} +\boldsymbol{{Rx}}^{\mathrm{2}} +\boldsymbol{{px}}+\boldsymbol{{q}}\right). \\ $$

Answered by mr W last updated on 16/Feb/19

Commented by mr W last updated on 16/Feb/19

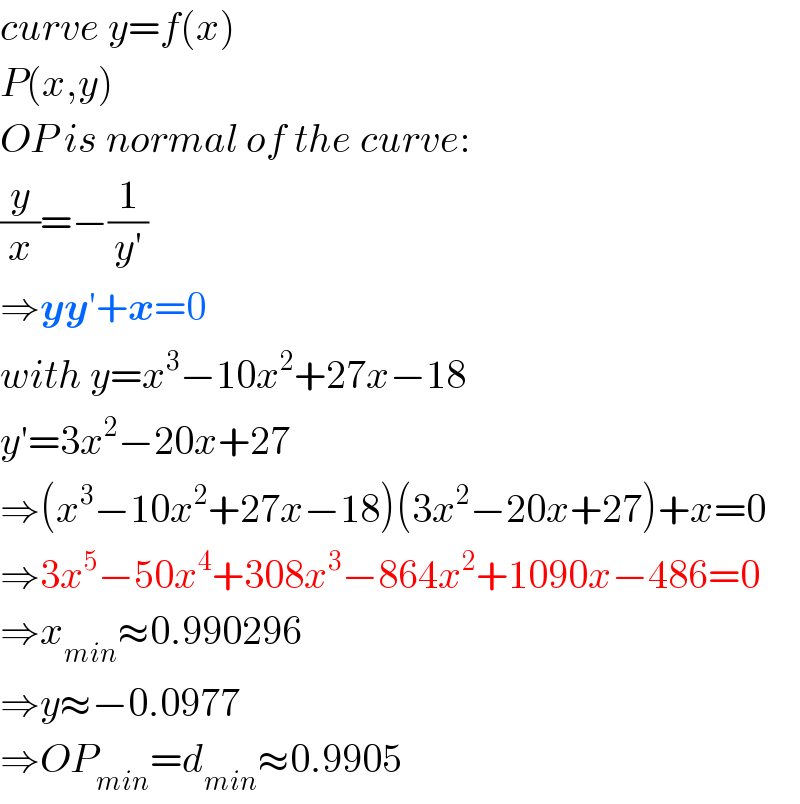
curve y=f(x) P(x,y) OP is normal of the curve: (y/x)=−(1/(y′)) ⇒yy′+x=0 with y=x^3 −10x^2 +27x−18 y′=3x^2 −20x+27 ⇒(x^3 −10x^2 +27x−18)(3x^2 −20x+27)+x=0 ⇒3x^5 −50x^4 +308x^3 −864x^2 +1090x−486=0 ⇒x_(min) ≈0.990296 ⇒y≈−0.0977 ⇒OP_(min) =d_(min) ≈0.9905

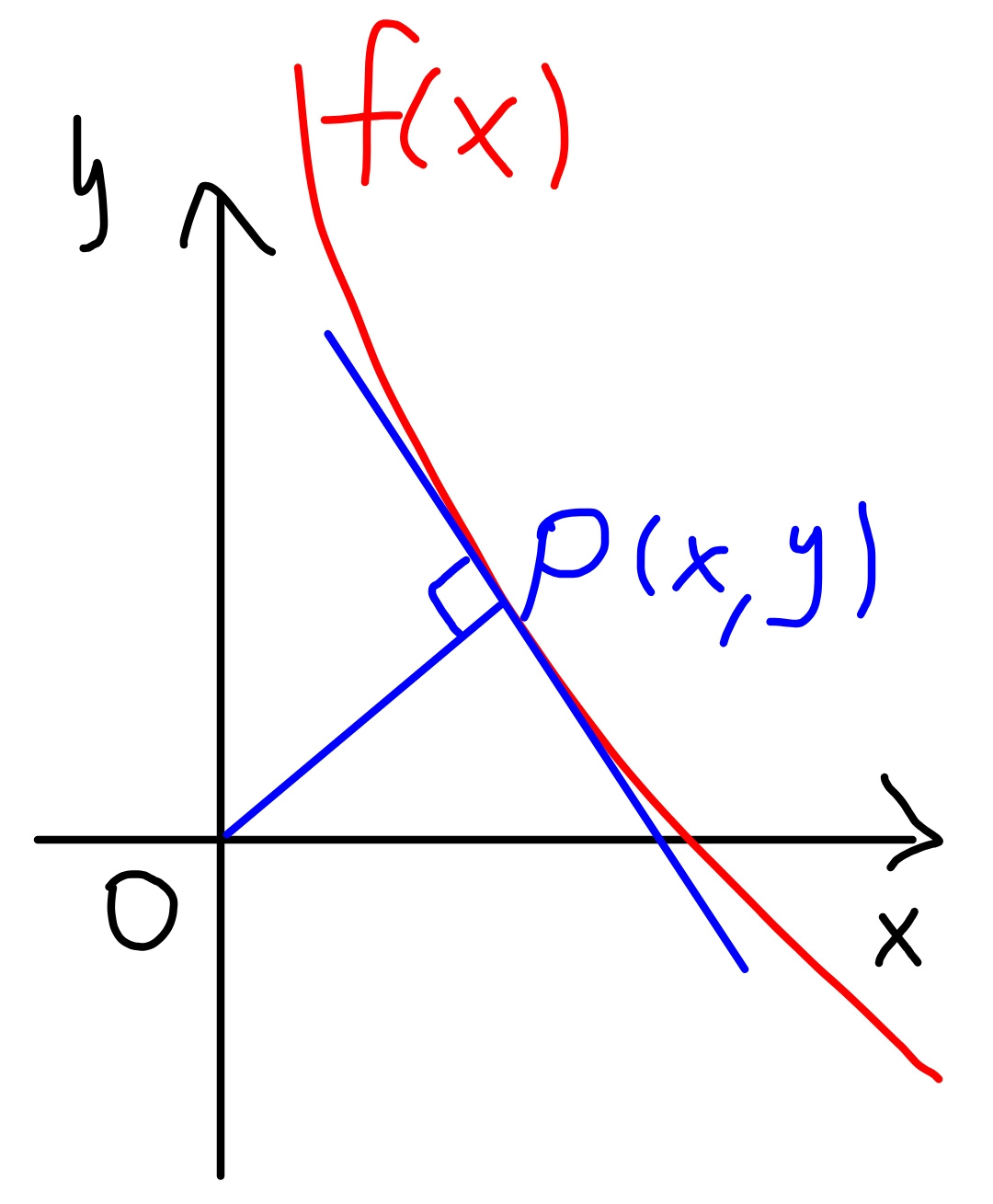
$${curve}\:{y}={f}\left({x}\right) \\ $$$${P}\left({x},{y}\right) \\ $$$${OP}\:{is}\:{normal}\:{of}\:{the}\:{curve}: \\ $$$$\frac{{y}}{{x}}=−\frac{\mathrm{1}}{{y}'} \\ $$$$\Rightarrow\boldsymbol{{yy}}'+\boldsymbol{{x}}=\mathrm{0} \\ $$$${with}\:{y}={x}^{\mathrm{3}} −\mathrm{10}{x}^{\mathrm{2}} +\mathrm{27}{x}−\mathrm{18} \\ $$$${y}'=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{20}{x}+\mathrm{27} \\ $$$$\Rightarrow\left({x}^{\mathrm{3}} −\mathrm{10}{x}^{\mathrm{2}} +\mathrm{27}{x}−\mathrm{18}\right)\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{20}{x}+\mathrm{27}\right)+{x}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}{x}^{\mathrm{5}} −\mathrm{50}{x}^{\mathrm{4}} +\mathrm{308}{x}^{\mathrm{3}} −\mathrm{864}{x}^{\mathrm{2}} +\mathrm{1090}{x}−\mathrm{486}=\mathrm{0} \\ $$$$\Rightarrow{x}_{{min}} \approx\mathrm{0}.\mathrm{990296} \\ $$$$\Rightarrow{y}\approx−\mathrm{0}.\mathrm{0977} \\ $$$$\Rightarrow{OP}_{{min}} ={d}_{{min}} \approx\mathrm{0}.\mathrm{9905} \\ $$

Commented by mr W last updated on 16/Feb/19

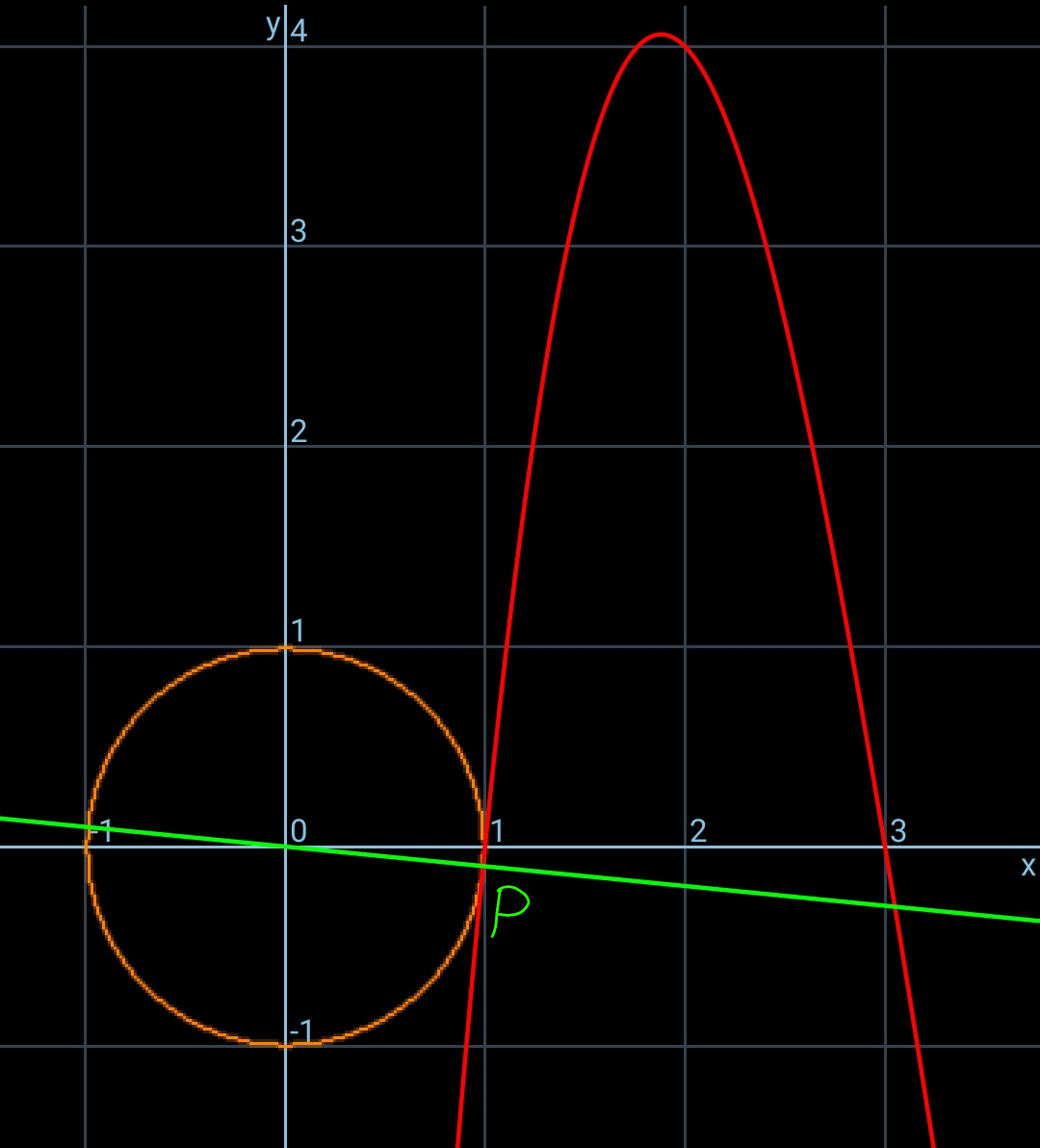
Commented by mr W last updated on 16/Feb/19

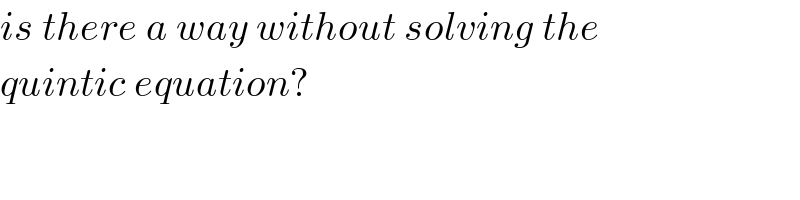
$${is}\:{there}\:{a}\:{way}\:{without}\:{solving}\:{the} \\ $$$${quintic}\:{equation}? \\ $$

Commented by mr W last updated on 16/Feb/19

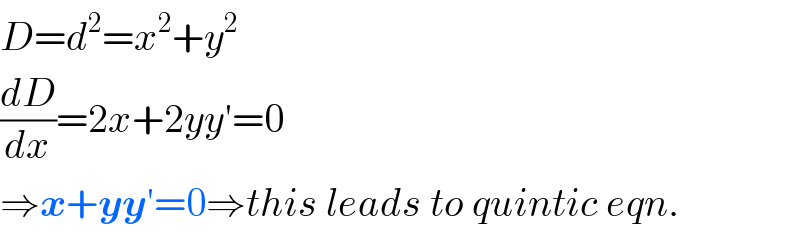
D=d^2 =x^2 +y^2 (dD/dx)=2x+2yy′=0 ⇒x+yy′=0⇒this leads to quintic eqn.

$${D}={d}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$\frac{{dD}}{{dx}}=\mathrm{2}{x}+\mathrm{2}{yy}'=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{{x}}+\boldsymbol{{yy}}'=\mathrm{0}\Rightarrow{this}\:{leads}\:{to}\:{quintic}\:{eqn}. \\ $$

Commented by MJS last updated on 16/Feb/19

no Sir. we can also go this way: (d/dx)[f(x)^2 +x^2 ]=0 which also leads to a quintic with at least no easy exact solution

$$\mathrm{no}\:\mathrm{Sir}. \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{also}\:\mathrm{go}\:\mathrm{this}\:\mathrm{way}: \\ $$$$\frac{{d}}{{dx}}\left[{f}\left({x}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} \right]=\mathrm{0} \\ $$$$\mathrm{which}\:\mathrm{also}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{quintic}\:\mathrm{with}\:\mathrm{at}\:\mathrm{least} \\ $$$$\mathrm{no}\:\mathrm{easy}\:\mathrm{exact}\:\mathrm{solution} \\ $$

Commented by ajfour last updated on 16/Feb/19

Beautiful demonstration Sir, thanks a lot. i think whatsoever we do it′ll land on solving a degree 5.

$${Beautiful}\:{demonstration}\:{Sir}, \\ $$$${thanks}\:{a}\:{lot}.\:{i}\:{think}\:{whatsoever} \\ $$$${we}\:{do}\:{it}'{ll}\:{land}\:{on}\:{solving}\:{a}\:{degree}\:\mathrm{5}. \\ $$

Facebook Tweet Pin

Find-shortest-distance-from-origin-to-the-cubic-y-x-3-10x-2-27x-18-

Leave a Reply Cancel reply