Menu Close

find-sin-cosx-x-2-x-1-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 100969 by mathmax by abdo last updated on 29/Jun/20
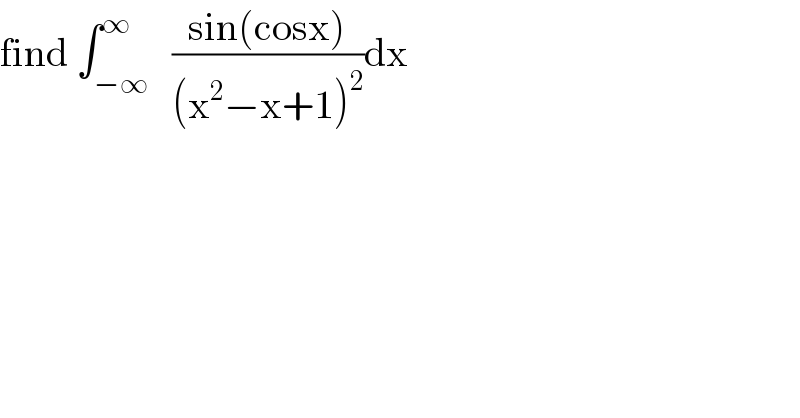
find ∫_(−∞) ^∞ ((sin(cosx))/((x^2 −x+1)^2 ))dx
$$\mathrm{find}\:\int_{−\infty} ^{\infty} \:\:\frac{\mathrm{sin}\left(\mathrm{cosx}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 30/Jun/20
I =∫_(−∞) ^(+∞ ) ((sin(cosx))/((x^2 −x+1)^2 ))dx ⇒I =Im(∫_(−∞) ^(+∞) (e^(icosx) /((x^2 −x+1)^2 ))dx) let ϕ(z) =(e^(icosz) /((z^2 −z+1)^2 )) poles of ϕ? z^2 −z+1 =0 →Δ =−3 ⇒z_1 =1+i(√3) =2e^((iπ)/3) z_2 =1−i(√3)=2e^(−((iπ)/3)) ⇒ϕ(z) =(e^(icosz) /((z−2e^((iπ)/3) )^2 (z+2e^(−((iπ)/3)) )^(2 ) )) the poles of ϕ are 2e^((iπ)/3) and 2 e^(−((iπ)/3)) (doubles) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,2e^((iπ)/3) ) Res(ϕ ,2e^((iπ)/3) ) =lim_(x→2 e^((iπ)/3) ) (1/((2−1)!)){ (z−e^((iπ)/3) )^2 ϕ(z)}^((1)) =lim_(z→2e^((iπ)/3) ) { (e^(icosz) /((z+2e^(−((iπ)/3)) )^2 ))}^((1)) =lim_(z→2e^((iπ)/3) ) {((−isinz e^(icosz) (z+2e^(−((iπ)/3)) )^2 −2(z+2e^(−((iπ)/3)) )e^(icosz) )/((z+2e^(−((iπ)/3)) )^4 ))} =lim_(z→2e^((iπ)/3) ) ((−isinz e^(icosz) (z+2e^(−((iπ)/3)) )−2 e^(icosz) )/((z+2e^(−((iπ)/3)) )^3 )) =lim_(z→ 2e^((iπ)/3) ) (({−isinz (z+2e^(−((iπ)/3)) )−2 }e^(icosz) )/((z+2e^(−((iπ)/3)) )^3 )) =(({−isin(2e^((iπ)/3) )(4cos((π/3))−2}e^(i cos(2e^((iπ)/3) )) )/(8(2cos((π/3))))) rest to finish the calculus...
$$\mathrm{I}\:=\int_{−\infty} ^{+\infty\:} \:\frac{\mathrm{sin}\left(\mathrm{cosx}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\:\Rightarrow\mathrm{I}\:=\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{icosx}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\right)\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{icosz}} }{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$$$\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta\:=−\mathrm{3}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}\:=\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \\ $$$$\mathrm{z}_{\mathrm{2}} =\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}=\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\Rightarrow\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{icosz}} }{\left(\mathrm{z}−\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}\:\:} }\:\:\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\varphi\:\mathrm{are} \\ $$$$\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{2}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\left(\mathrm{doubles}\right)\:\:\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give}\: \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right) \\ $$$$\mathrm{Res}\left(\varphi\:,\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{2}\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\:\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} \:\varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\left\{\:\frac{\mathrm{e}^{\mathrm{icosz}} }{\left(\mathrm{z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \: \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\:\left\{\frac{−\mathrm{isinz}\:\mathrm{e}^{\mathrm{icosz}} \left(\mathrm{z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\mathrm{e}^{\mathrm{icosz}} }{\left(\mathrm{z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} }\right\} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\frac{−\mathrm{isinz}\:\mathrm{e}^{\mathrm{icosz}} \left(\mathrm{z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)−\mathrm{2}\:\mathrm{e}^{\mathrm{icosz}} }{\left(\mathrm{z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} } \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\:\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\:\:\frac{\left\{−\mathrm{isinz}\:\left(\mathrm{z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)−\mathrm{2}\:\right\}\mathrm{e}^{\mathrm{icosz}} }{\left(\mathrm{z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} } \\ $$$$=\frac{\left\{−\mathrm{isin}\left(\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{4cos}\left(\frac{\pi}{\mathrm{3}}\right)−\mathrm{2}\right\}\mathrm{e}^{\mathrm{i}\:\mathrm{cos}\left(\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)} \right.}{\mathrm{8}\left(\mathrm{2cos}\left(\frac{\pi}{\mathrm{3}}\right)\right)}\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{finish}\:\mathrm{the}\:\mathrm{calculus}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *