Question Number 117606 by TANMAY PANACEA last updated on 12/Oct/20
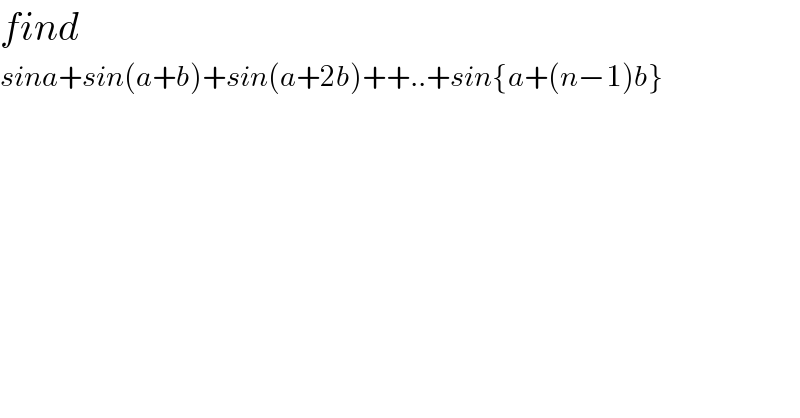
$${find} \\ $$$${sina}+{sin}\left({a}+{b}\right)+{sin}\left({a}+\mathrm{2}{b}\right)++..+{sin}\left\{{a}+\left({n}−\mathrm{1}\right){b}\right\} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Oct/20
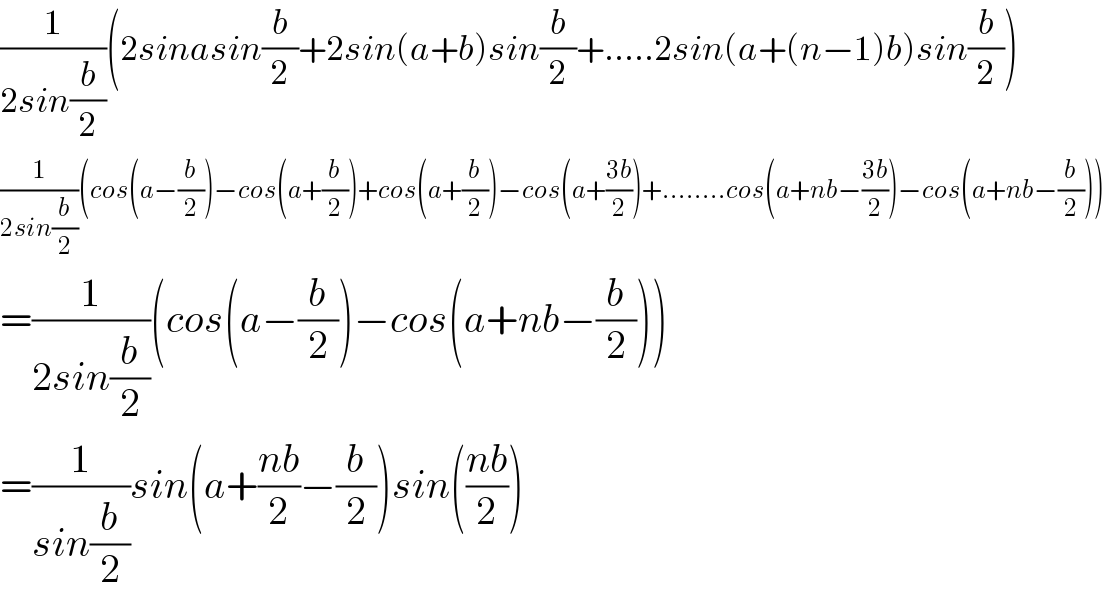
$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{{b}}{\mathrm{2}}}\left(\mathrm{2}{sinasin}\frac{{b}}{\mathrm{2}}+\mathrm{2}{sin}\left({a}+{b}\right){sin}\frac{{b}}{\mathrm{2}}+…..\mathrm{2}{sin}\left({a}+\left({n}−\mathrm{1}\right){b}\right){sin}\frac{{b}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{{b}}{\mathrm{2}}}\left({cos}\left({a}−\frac{{b}}{\mathrm{2}}\right)−{cos}\left({a}+\frac{{b}}{\mathrm{2}}\right)+{cos}\left({a}+\frac{{b}}{\mathrm{2}}\right)−{cos}\left({a}+\frac{\mathrm{3}{b}}{\mathrm{2}}\right)+……..{cos}\left({a}+{nb}−\frac{\mathrm{3}{b}}{\mathrm{2}}\right)−{cos}\left({a}+{nb}−\frac{{b}}{\mathrm{2}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{{b}}{\mathrm{2}}}\left({cos}\left({a}−\frac{{b}}{\mathrm{2}}\right)−{cos}\left({a}+{nb}−\frac{{b}}{\mathrm{2}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{{sin}\frac{{b}}{\mathrm{2}}}{sin}\left({a}+\frac{{nb}}{\mathrm{2}}−\frac{{b}}{\mathrm{2}}\right){sin}\left(\frac{{nb}}{\mathrm{2}}\right) \\ $$
Commented by TANMAY PANACEA last updated on 12/Oct/20

$${bah}\:{darun}… \\ $$
Commented by Dwaipayan Shikari last updated on 12/Oct/20
ধন্যবাদ
Commented by Dwaipayan Shikari last updated on 12/Oct/20
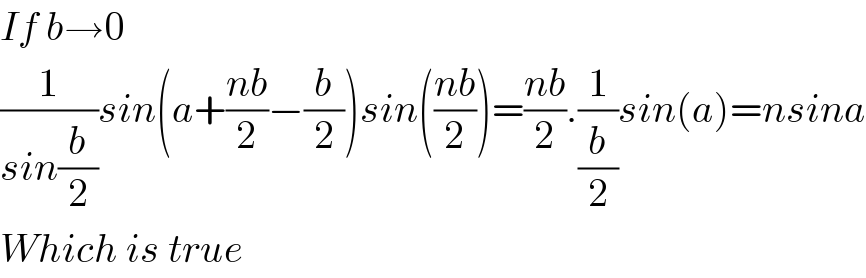
$${If}\:{b}\rightarrow\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{sin}\frac{{b}}{\mathrm{2}}}{sin}\left({a}+\frac{{nb}}{\mathrm{2}}−\frac{{b}}{\mathrm{2}}\right){sin}\left(\frac{{nb}}{\mathrm{2}}\right)=\frac{{nb}}{\mathrm{2}}.\frac{\mathrm{1}}{\frac{{b}}{\mathrm{2}}}{sin}\left({a}\right)={nsina} \\ $$$${Which}\:{is}\:{true} \\ $$
Answered by mathmax by abdo last updated on 12/Oct/20

$$\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \mathrm{sin}\left(\mathrm{a}+\mathrm{kb}\right)\:\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\mathrm{Im}\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \mathrm{e}^{\mathrm{i}\left(\mathrm{a}+\mathrm{kb}\right)} \right) \\ $$$$\sum_{\mathrm{k}=\mathrm{0}\:} ^{\mathrm{n}−\mathrm{1}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{a}+\mathrm{kb}\right)} \:=\mathrm{e}^{\mathrm{ia}} \:\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\left(\mathrm{e}^{\mathrm{ib}} \right)^{\mathrm{k}} \:=\mathrm{e}^{\mathrm{ia}} ×\frac{\mathrm{1}−\left(\mathrm{e}^{\mathrm{ib}} \right)^{\mathrm{n}} }{\mathrm{1}−\mathrm{e}^{\mathrm{ib}} } \\ $$$$=\mathrm{e}^{\mathrm{ia}} ×\frac{\mathrm{1}−\mathrm{e}^{\mathrm{inb}} }{\mathrm{1}−\mathrm{cosb}−\mathrm{isinb}}\:=\mathrm{e}^{\mathrm{ia}} ×\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{nb}\right)−\mathrm{isin}\left(\mathrm{nb}\right)}{\mathrm{1}−\mathrm{cosb}−\mathrm{isinb}} \\ $$$$=\mathrm{e}^{\mathrm{ia}} .\frac{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{nb}}{\mathrm{2}}\right)−\mathrm{2isin}\left(\frac{\mathrm{nb}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{nb}}{\mathrm{2}}\right)}{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{b}}{\mathrm{2}}\right)−\mathrm{2isin}\left(\frac{\mathrm{b}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{b}}{\mathrm{2}}\right)} \\ $$$$=\mathrm{e}^{\mathrm{ia}} ×\frac{−\mathrm{isin}\left(\frac{\mathrm{nb}}{\mathrm{2}}\right)\:\mathrm{e}^{\mathrm{i}\frac{\mathrm{nb}}{\mathrm{2}}} }{−\mathrm{isin}\left(\frac{\mathrm{b}}{\mathrm{2}}\right)\mathrm{e}^{\frac{\mathrm{ib}}{\mathrm{2}}} }\:=\frac{\mathrm{sin}\left(\frac{\mathrm{nb}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\mathrm{b}}{\mathrm{2}}\right)}\mathrm{e}^{\mathrm{ia}} ×\mathrm{e}^{\mathrm{i}\frac{\left(\mathrm{n}−\mathrm{1}\right)\mathrm{b}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{sin}\left(\frac{\mathrm{nb}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\mathrm{b}}{\mathrm{2}}\right)}×\:\mathrm{e}^{\mathrm{i}\left(\mathrm{a}+\frac{\left(\mathrm{n}−\mathrm{1}\right)\mathrm{b}}{\mathrm{2}}\right)} \:\Rightarrow\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{sin}\left(\frac{\mathrm{nb}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\mathrm{b}}{\mathrm{2}}\right)}×\mathrm{sin}\left(\mathrm{a}+\frac{\left(\mathrm{n}−\mathrm{1}\right)\mathrm{b}}{\mathrm{2}}\right) \\ $$
