Question Number 86701 by john santu last updated on 30/Mar/20
![find solution 4^(sin x −(1/4)) − (1/(2+(√2))) .2^(sin x) −1 = 0 in x ∈[ 0,2π ]](https://www.tinkutara.com/question/Q86701.png)
$$\mathrm{find}\:\mathrm{solution}\: \\ $$$$\mathrm{4}^{\mathrm{sin}\:\mathrm{x}\:−\frac{\mathrm{1}}{\mathrm{4}}} \:−\:\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:.\mathrm{2}^{\mathrm{sin}\:\mathrm{x}} \:−\mathrm{1}\:=\:\mathrm{0}\: \\ $$$$\mathrm{in}\:\mathrm{x}\:\in\left[\:\mathrm{0},\mathrm{2}\pi\:\right]\: \\ $$
Commented by john santu last updated on 30/Mar/20
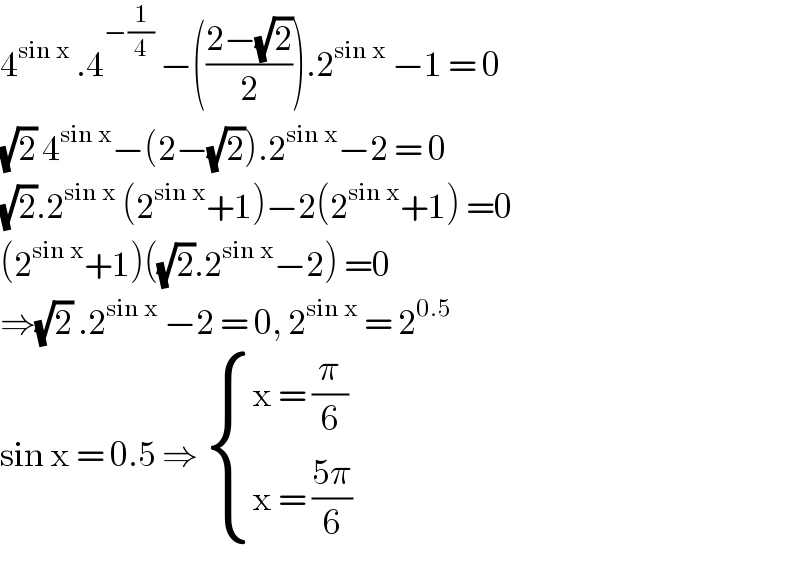
$$\mathrm{4}^{\mathrm{sin}\:\mathrm{x}} \:.\mathrm{4}^{−\frac{\mathrm{1}}{\mathrm{4}}} \:−\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}}\right).\mathrm{2}^{\mathrm{sin}\:\mathrm{x}} \:−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\sqrt{\mathrm{2}}\:\mathrm{4}^{\mathrm{sin}\:\mathrm{x}} −\left(\mathrm{2}−\sqrt{\mathrm{2}}\right).\mathrm{2}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{2}\:=\:\mathrm{0} \\ $$$$\sqrt{\mathrm{2}}.\mathrm{2}^{\mathrm{sin}\:\mathrm{x}} \:\left(\mathrm{2}^{\mathrm{sin}\:\mathrm{x}} +\mathrm{1}\right)−\mathrm{2}\left(\mathrm{2}^{\mathrm{sin}\:\mathrm{x}} +\mathrm{1}\right)\:=\mathrm{0} \\ $$$$\left(\mathrm{2}^{\mathrm{sin}\:\mathrm{x}} +\mathrm{1}\right)\left(\sqrt{\mathrm{2}}.\mathrm{2}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{2}\right)\:=\mathrm{0} \\ $$$$\Rightarrow\sqrt{\mathrm{2}}\:.\mathrm{2}^{\mathrm{sin}\:\mathrm{x}} \:−\mathrm{2}\:=\:\mathrm{0},\:\mathrm{2}^{\mathrm{sin}\:\mathrm{x}} \:=\:\mathrm{2}^{\mathrm{0}.\mathrm{5}} \\ $$$$\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{0}.\mathrm{5}\:\Rightarrow\:\begin{cases}{\mathrm{x}\:=\:\frac{\pi}{\mathrm{6}}}\\{\mathrm{x}\:=\:\frac{\mathrm{5}\pi}{\mathrm{6}}}\end{cases} \\ $$
