Question Number 125691 by fajri last updated on 13/Dec/20

$${find}\:{solution}\:: \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}\:} }\:+\:\mathrm{4}\frac{{dy}}{{dx}}\:=\:\mathrm{3}\:{cosec}\:\theta \\ $$
Answered by mathmax by abdo last updated on 14/Dec/20
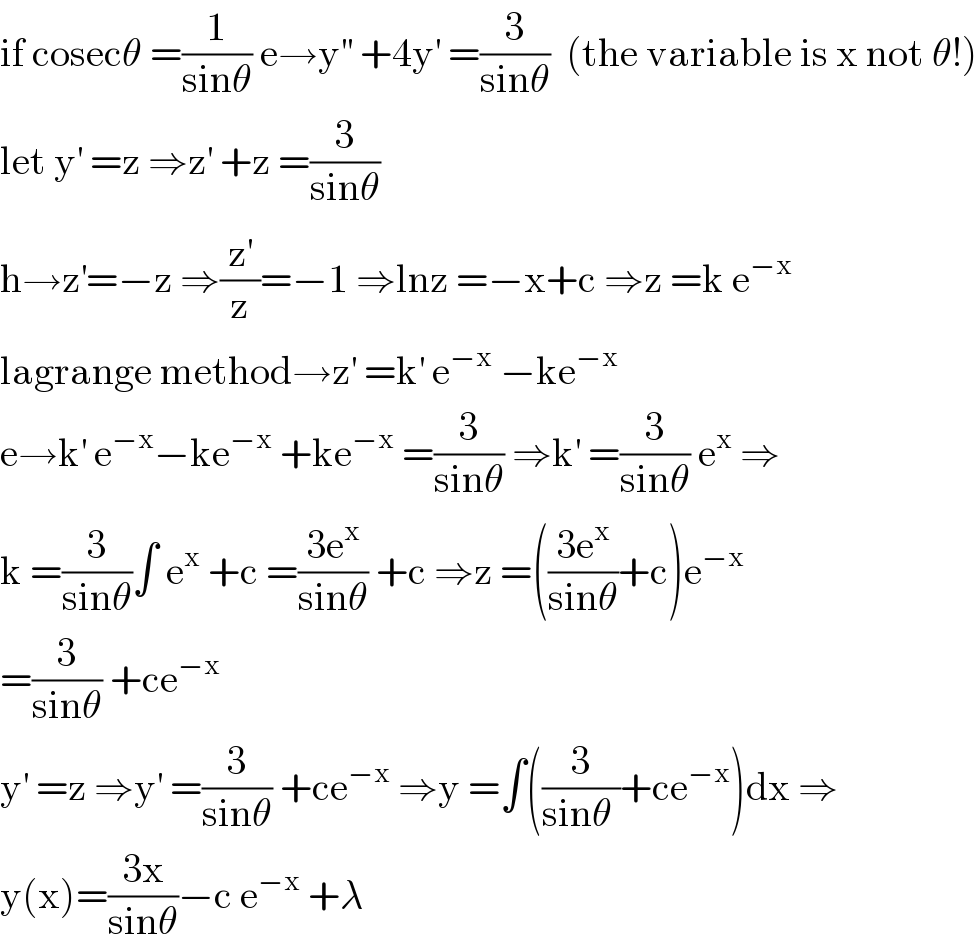
$$\mathrm{if}\:\mathrm{cosec}\theta\:=\frac{\mathrm{1}}{\mathrm{sin}\theta}\:\mathrm{e}\rightarrow\mathrm{y}^{''} \:+\mathrm{4y}^{'} \:=\frac{\mathrm{3}}{\mathrm{sin}\theta}\:\:\left(\mathrm{the}\:\mathrm{variable}\:\mathrm{is}\:\mathrm{x}\:\mathrm{not}\:\theta!\right) \\ $$$$\mathrm{let}\:\mathrm{y}^{'} \:=\mathrm{z}\:\Rightarrow\mathrm{z}^{'} \:+\mathrm{z}\:=\frac{\mathrm{3}}{\mathrm{sin}\theta} \\ $$$$\mathrm{h}\rightarrow\mathrm{z}^{'} =−\mathrm{z}\:\Rightarrow\frac{\mathrm{z}^{'} }{\mathrm{z}}=−\mathrm{1}\:\Rightarrow\mathrm{lnz}\:=−\mathrm{x}+\mathrm{c}\:\Rightarrow\mathrm{z}\:=\mathrm{k}\:\mathrm{e}^{−\mathrm{x}} \\ $$$$\mathrm{lagrange}\:\mathrm{method}\rightarrow\mathrm{z}^{'} \:=\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{x}} \:−\mathrm{ke}^{−\mathrm{x}} \\ $$$$\mathrm{e}\rightarrow\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{x}} −\mathrm{ke}^{−\mathrm{x}} \:+\mathrm{ke}^{−\mathrm{x}} \:=\frac{\mathrm{3}}{\mathrm{sin}\theta}\:\Rightarrow\mathrm{k}^{'} \:=\frac{\mathrm{3}}{\mathrm{sin}\theta}\:\mathrm{e}^{\mathrm{x}} \:\Rightarrow \\ $$$$\mathrm{k}\:=\frac{\mathrm{3}}{\mathrm{sin}\theta}\int\:\mathrm{e}^{\mathrm{x}} \:+\mathrm{c}\:=\frac{\mathrm{3e}^{\mathrm{x}} }{\mathrm{sin}\theta}\:+\mathrm{c}\:\Rightarrow\mathrm{z}\:=\left(\frac{\mathrm{3e}^{\mathrm{x}} }{\mathrm{sin}\theta}+\mathrm{c}\right)\mathrm{e}^{−\mathrm{x}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{sin}\theta}\:+\mathrm{ce}^{−\mathrm{x}} \\ $$$$\mathrm{y}^{'} \:=\mathrm{z}\:\Rightarrow\mathrm{y}^{'} \:=\frac{\mathrm{3}}{\mathrm{sin}\theta}\:+\mathrm{ce}^{−\mathrm{x}} \:\Rightarrow\mathrm{y}\:=\int\left(\frac{\mathrm{3}}{\mathrm{sin}\theta\:}+\mathrm{ce}^{−\mathrm{x}} \right)\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\frac{\mathrm{3x}}{\mathrm{sin}\theta}−\mathrm{c}\:\mathrm{e}^{−\mathrm{x}} \:+\lambda \\ $$
