Question Number 63291 by aliesam last updated on 02/Jul/19
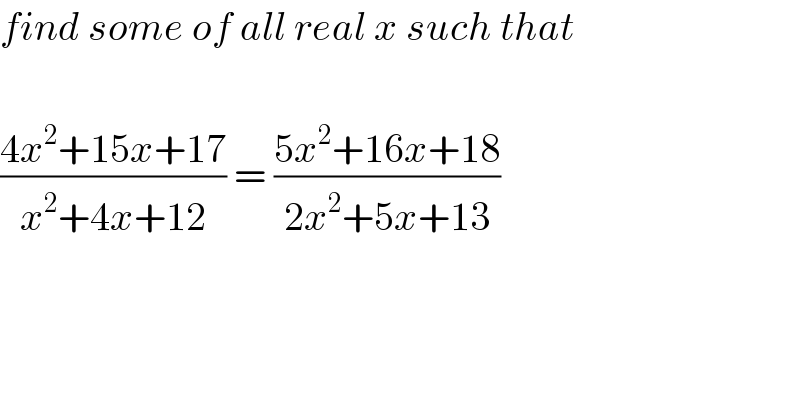
$${find}\:{some}\:{of}\:{all}\:{real}\:{x}\:{such}\:{that} \\ $$$$ \\ $$$$\frac{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{17}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{12}}\:=\:\frac{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{16}{x}+\mathrm{18}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{13}} \\ $$
Commented by Prithwish sen last updated on 02/Jul/19

$$\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{5x}+\mathrm{13}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{12}}\:=\:\frac{\mathrm{5x}^{\mathrm{2}} +\mathrm{16x}+\mathrm{18}}{\mathrm{4x}^{\mathrm{2}} +\mathrm{15x}+\mathrm{17}} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{12}}\:=\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}{\mathrm{4x}^{\mathrm{2}} +\mathrm{15x}+\mathrm{17}} \\ $$$$\mathrm{either}\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{or}\:\mathrm{4x}^{\mathrm{2}} +\mathrm{15x}+\mathrm{17}−\mathrm{x}^{\mathrm{2}} −\mathrm{4x}−\mathrm{12}\:=\mathrm{0} \\ $$$$\mathrm{3x}^{\mathrm{2}} +\mathrm{11x}+\mathrm{5}=\mathrm{0} \\ $$$$\therefore\:\mathrm{x}\:=\:\frac{−\mathrm{1}\pm\sqrt{−\mathrm{3}}}{\mathrm{2}}\:,\:\frac{−\mathrm{11}\pm\sqrt{\mathrm{61}}}{\mathrm{6}} \\ $$$$\mathrm{please}\:\mathrm{check} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by aliesam last updated on 02/Jul/19

$${well}\:{done}\:{sir} \\ $$
Commented by Prithwish sen last updated on 02/Jul/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
