Question Number 150500 by EnterUsername last updated on 13/Aug/21
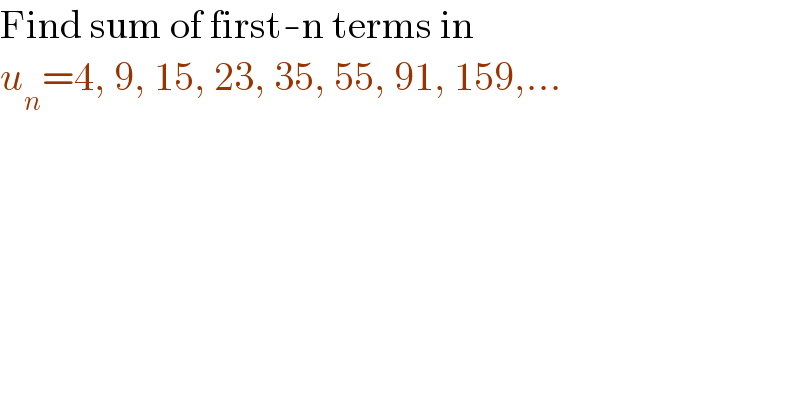
$$\mathrm{Find}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{first}-\mathrm{n}\:\mathrm{terms}\:\mathrm{in} \\ $$$${u}_{{n}} =\mathrm{4},\:\mathrm{9},\:\mathrm{15},\:\mathrm{23},\:\mathrm{35},\:\mathrm{55},\:\mathrm{91},\:\mathrm{159},… \\ $$
Commented by CAIMAN last updated on 13/Aug/21
Un=2^n-1+4n -1
Answered by Ar Brandon last updated on 13/Aug/21
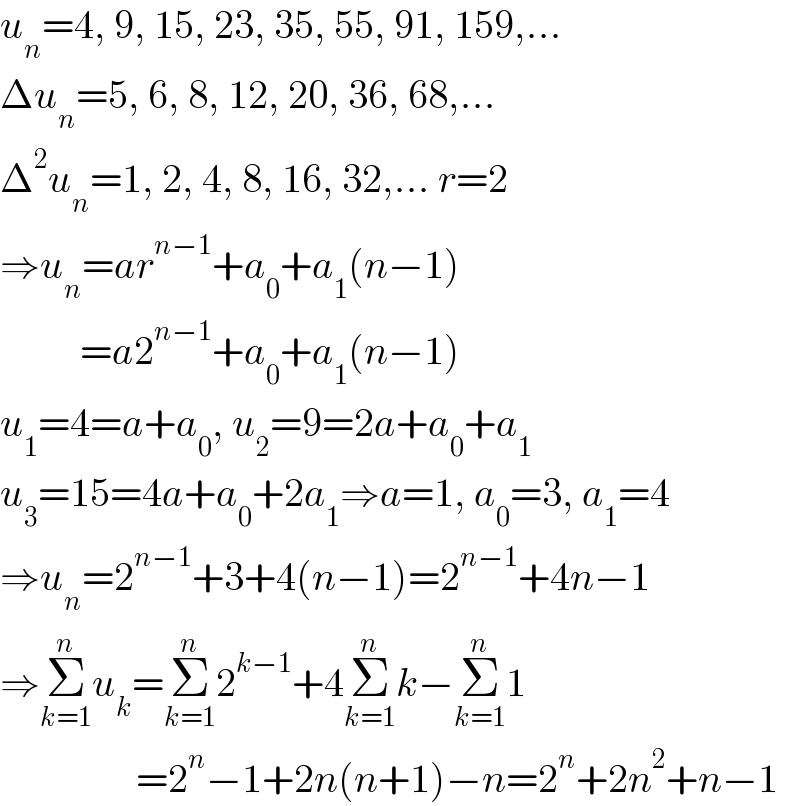
$${u}_{{n}} =\mathrm{4},\:\mathrm{9},\:\mathrm{15},\:\mathrm{23},\:\mathrm{35},\:\mathrm{55},\:\mathrm{91},\:\mathrm{159},… \\ $$$$\Delta{u}_{{n}} =\mathrm{5},\:\mathrm{6},\:\mathrm{8},\:\mathrm{12},\:\mathrm{20},\:\mathrm{36},\:\mathrm{68},… \\ $$$$\Delta^{\mathrm{2}} {u}_{{n}} =\mathrm{1},\:\mathrm{2},\:\mathrm{4},\:\mathrm{8},\:\mathrm{16},\:\mathrm{32},…\:{r}=\mathrm{2} \\ $$$$\Rightarrow{u}_{{n}} ={ar}^{{n}−\mathrm{1}} +{a}_{\mathrm{0}} +{a}_{\mathrm{1}} \left({n}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:={a}\mathrm{2}^{{n}−\mathrm{1}} +{a}_{\mathrm{0}} +{a}_{\mathrm{1}} \left({n}−\mathrm{1}\right) \\ $$$${u}_{\mathrm{1}} =\mathrm{4}={a}+{a}_{\mathrm{0}} ,\:{u}_{\mathrm{2}} =\mathrm{9}=\mathrm{2}{a}+{a}_{\mathrm{0}} +{a}_{\mathrm{1}} \\ $$$${u}_{\mathrm{3}} =\mathrm{15}=\mathrm{4}{a}+{a}_{\mathrm{0}} +\mathrm{2}{a}_{\mathrm{1}} \Rightarrow{a}=\mathrm{1},\:{a}_{\mathrm{0}} =\mathrm{3},\:{a}_{\mathrm{1}} =\mathrm{4} \\ $$$$\Rightarrow{u}_{{n}} =\mathrm{2}^{{n}−\mathrm{1}} +\mathrm{3}+\mathrm{4}\left({n}−\mathrm{1}\right)=\mathrm{2}^{{n}−\mathrm{1}} +\mathrm{4}{n}−\mathrm{1} \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{u}_{{k}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}−\mathrm{1}} +\mathrm{4}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{{n}} −\mathrm{1}+\mathrm{2}{n}\left({n}+\mathrm{1}\right)−{n}=\mathrm{2}^{{n}} +\mathrm{2}{n}^{\mathrm{2}} +{n}−\mathrm{1} \\ $$
