Question Number 31456 by rahul 19 last updated on 08/Mar/18
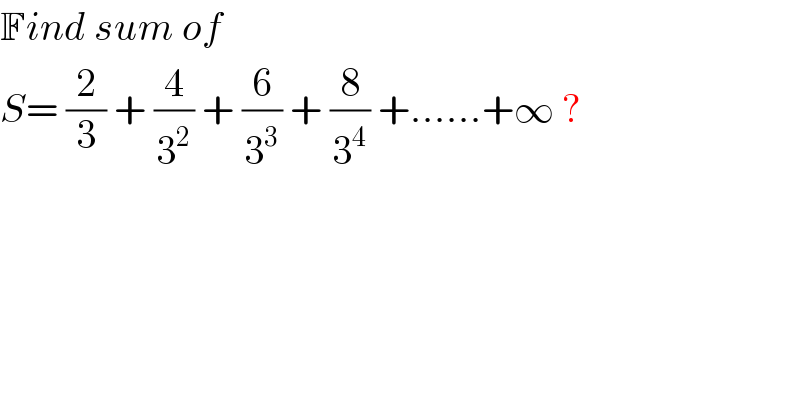
$$\mathbb{F}{ind}\:{sum}\:{of} \\ $$$${S}=\:\frac{\mathrm{2}}{\mathrm{3}}\:+\:\frac{\mathrm{4}}{\mathrm{3}^{\mathrm{2}} }\:+\:\frac{\mathrm{6}}{\mathrm{3}^{\mathrm{3}} }\:+\:\frac{\mathrm{8}}{\mathrm{3}^{\mathrm{4}} }\:+……+\infty\:? \\ $$
Commented by MJS last updated on 08/Mar/18
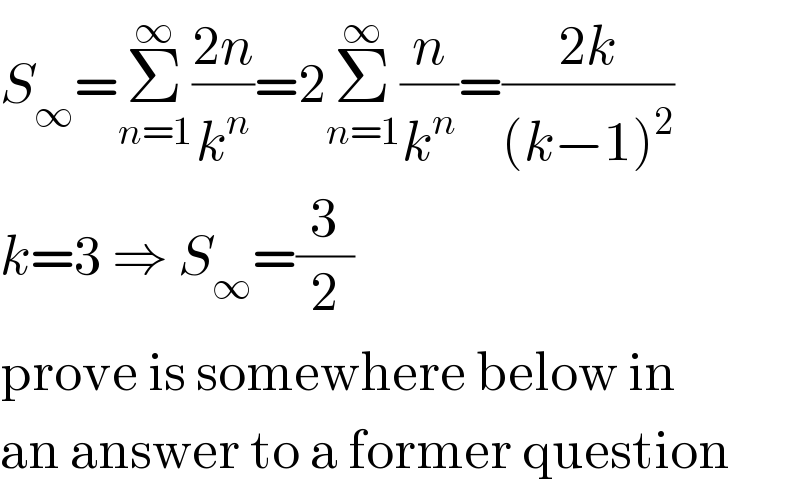
$${S}_{\infty} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}}{{k}^{{n}} }=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{{k}^{{n}} }=\frac{\mathrm{2}{k}}{\left({k}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${k}=\mathrm{3}\:\Rightarrow\:{S}_{\infty} =\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{prove}\:\mathrm{is}\:\mathrm{somewhere}\:\mathrm{below}\:\mathrm{in} \\ $$$$\mathrm{an}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{a}\:\mathrm{former}\:\mathrm{question} \\ $$
Commented by rahul 19 last updated on 09/Mar/18

$${thank}\:{u}\:{sir}! \\ $$
