Question Number 173677 by naka3546 last updated on 16/Jul/22
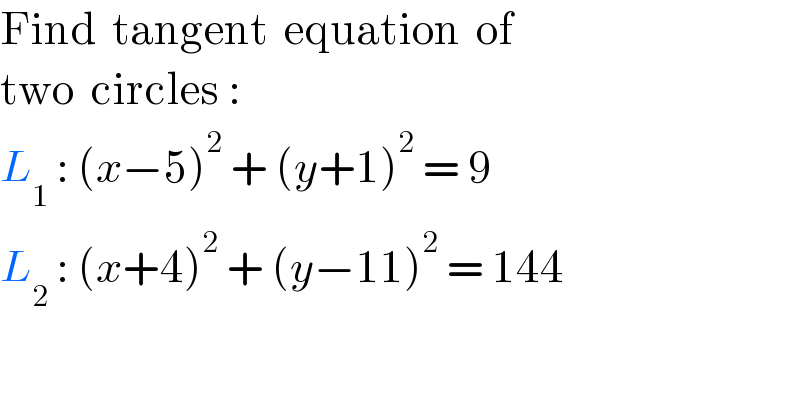
$$\mathrm{Find}\:\:\mathrm{tangent}\:\:\mathrm{equation}\:\:\mathrm{of}\:\: \\ $$$$\mathrm{two}\:\:\mathrm{circles}\:: \\ $$$${L}_{\mathrm{1}} \::\:\left({x}−\mathrm{5}\right)^{\mathrm{2}} \:+\:\left({y}+\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{9} \\ $$$${L}_{\mathrm{2}} \::\:\left({x}+\mathrm{4}\right)^{\mathrm{2}} \:+\:\left({y}−\mathrm{11}\right)^{\mathrm{2}} \:=\:\mathrm{144} \\ $$
Commented by kaivan.ahmadi last updated on 16/Jul/22
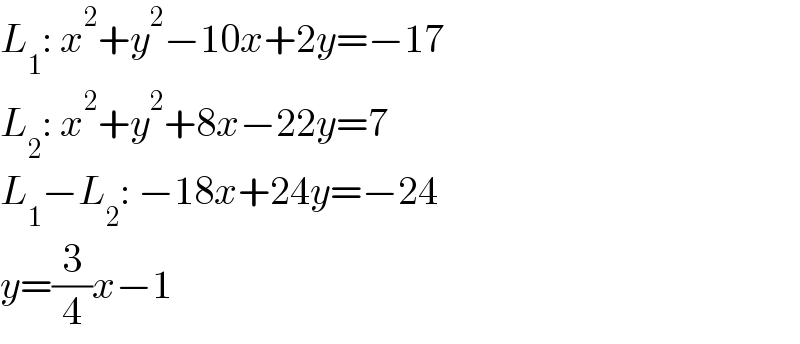
$${L}_{\mathrm{1}} :\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{2}{y}=−\mathrm{17} \\ $$$${L}_{\mathrm{2}} :\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{22}{y}=\mathrm{7} \\ $$$${L}_{\mathrm{1}} −{L}_{\mathrm{2}} :\:−\mathrm{18}{x}+\mathrm{24}{y}=−\mathrm{24} \\ $$$${y}=\frac{\mathrm{3}}{\mathrm{4}}{x}−\mathrm{1} \\ $$
Commented by naka3546 last updated on 16/Jul/22
$$\mathrm{Thank}\:\:\mathrm{you},\:\mathrm{sir}. \\ $$
