Question Number 58168 by maxmathsup by imad last updated on 19/Apr/19
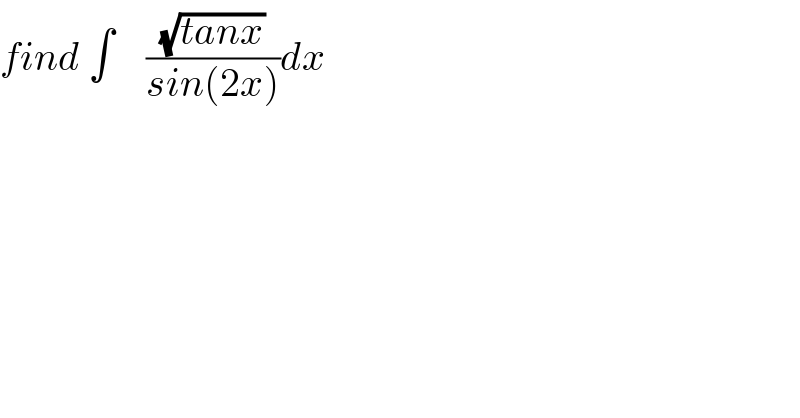
$${find}\:\int\:\:\:\:\frac{\sqrt{{tanx}}}{{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$
Answered by tanmay last updated on 19/Apr/19
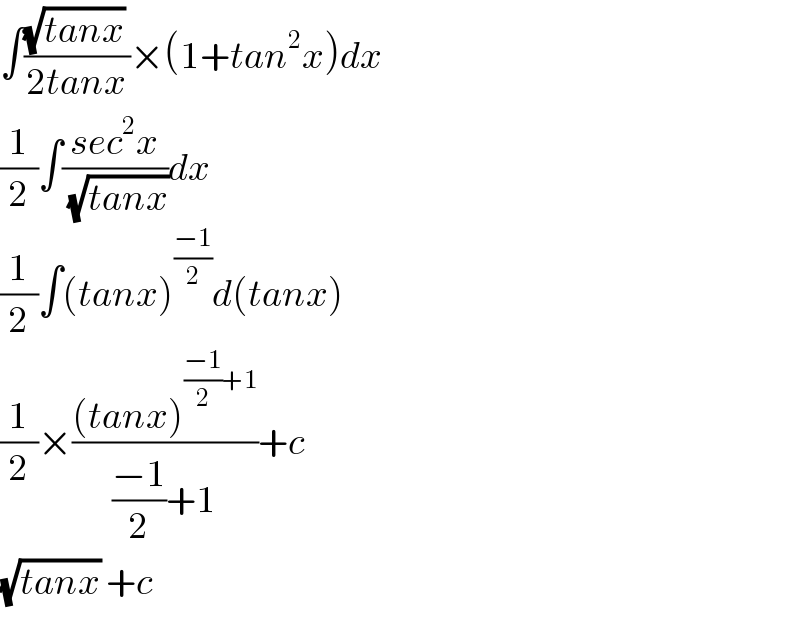
$$\int\frac{\sqrt{{tanx}}\:}{\mathrm{2}{tanx}}×\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right){dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sec}^{\mathrm{2}} {x}}{\:\sqrt{{tanx}}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\left({tanx}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} {d}\left({tanx}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\left({tanx}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} }{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}}+{c} \\ $$$$\sqrt{{tanx}}\:+{c} \\ $$
Commented by maxmathsup by imad last updated on 19/Apr/19

$${thanks}\:{sir} \\ $$
Answered by malwaan last updated on 19/Apr/19
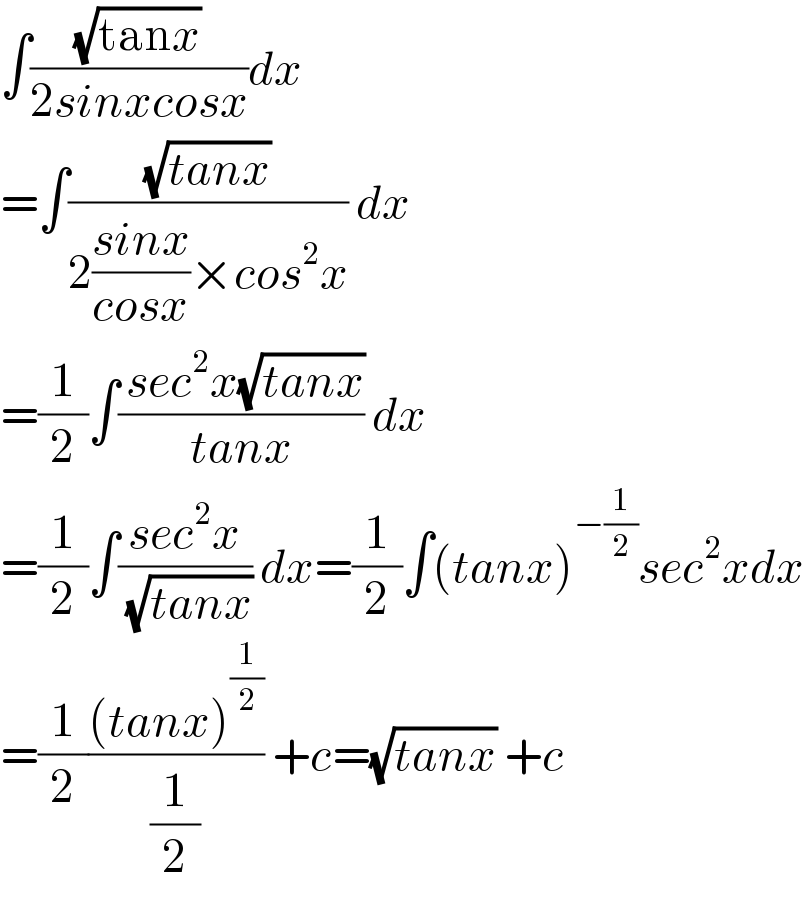
$$\int\frac{\sqrt{\mathrm{tan}{x}}}{\mathrm{2}{sinxcosx}}{dx} \\ $$$$=\int\frac{\sqrt{{tanx}}}{\mathrm{2}\frac{{sinx}}{{cosx}}×{cos}^{\mathrm{2}} {x}}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\:{sec}^{\mathrm{2}} {x}\sqrt{{tanx}}}{{tanx}}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sec}^{\mathrm{2}} {x}}{\:\sqrt{{tanx}}}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\left({tanx}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {sec}^{\mathrm{2}} {xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{\left({tanx}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\frac{\mathrm{1}}{\mathrm{2}}}\:+{c}=\sqrt{{tanx}}\:+{c} \\ $$
Commented by maxmathsup by imad last updated on 19/Apr/19

$${thanks}\:{sir} \\ $$
