Question Number 79626 by M±th+et£s last updated on 26/Jan/20
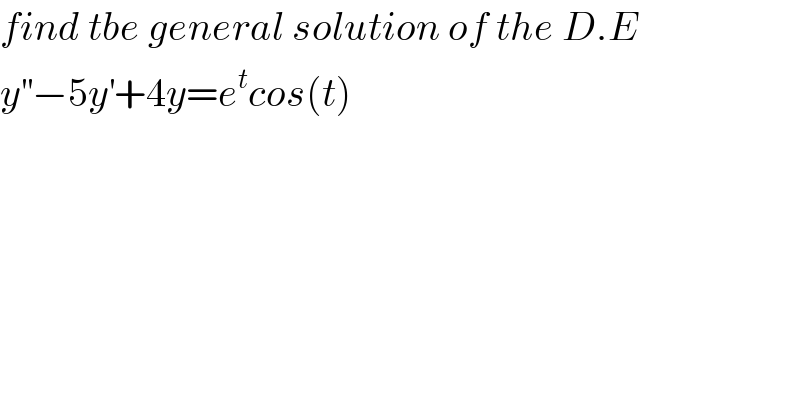
$${find}\:{tbe}\:{general}\:{solution}\:{of}\:{the}\:{D}.{E} \\ $$$${y}^{''} −\mathrm{5}{y}^{'} +\mathrm{4}{y}={e}^{{t}} {cos}\left({t}\right) \\ $$
Answered by mind is power last updated on 27/Jan/20
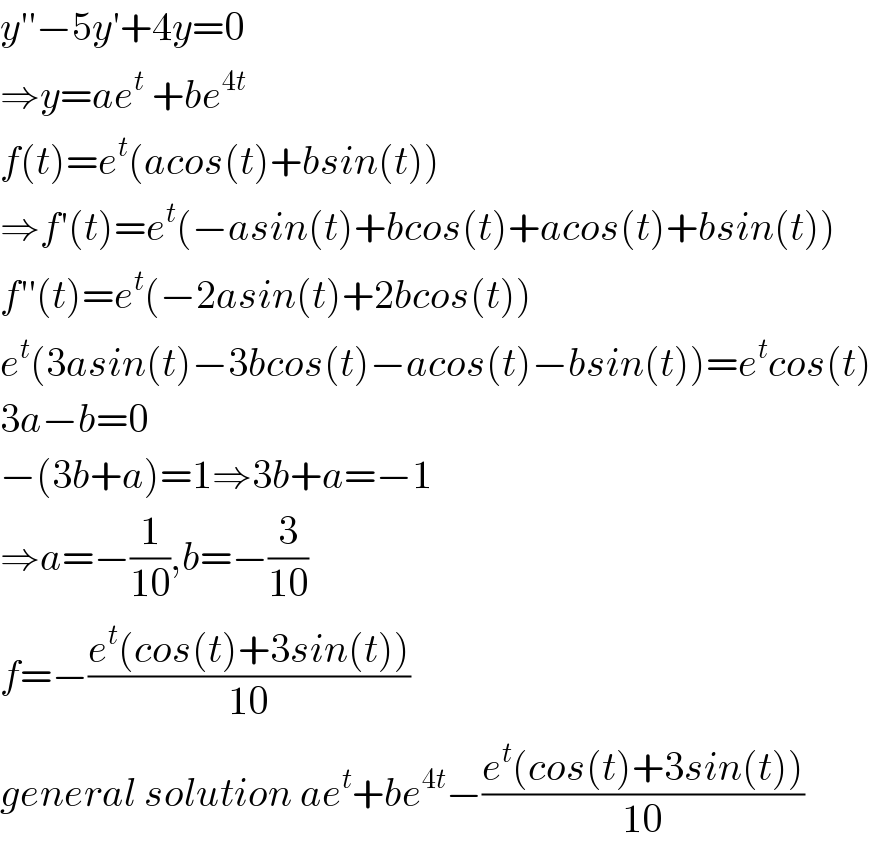
$${y}''−\mathrm{5}{y}'+\mathrm{4}{y}=\mathrm{0} \\ $$$$\Rightarrow{y}={ae}^{{t}} \:+{be}^{\mathrm{4}{t}} \\ $$$${f}\left({t}\right)={e}^{{t}} \left({acos}\left({t}\right)+{bsin}\left({t}\right)\right) \\ $$$$\Rightarrow{f}'\left({t}\right)={e}^{{t}} \left(−{asin}\left({t}\right)+{bcos}\left({t}\right)+{acos}\left({t}\right)+{bsin}\left({t}\right)\right) \\ $$$${f}''\left({t}\right)={e}^{{t}} \left(−\mathrm{2}{asin}\left({t}\right)+\mathrm{2}{bcos}\left({t}\right)\right) \\ $$$${e}^{{t}} \left(\mathrm{3}{asin}\left({t}\right)−\mathrm{3}{bcos}\left({t}\right)−{acos}\left({t}\right)−{bsin}\left({t}\right)\right)={e}^{{t}} {cos}\left({t}\right) \\ $$$$\mathrm{3}{a}−{b}=\mathrm{0} \\ $$$$−\left(\mathrm{3}{b}+{a}\right)=\mathrm{1}\Rightarrow\mathrm{3}{b}+{a}=−\mathrm{1} \\ $$$$\Rightarrow{a}=−\frac{\mathrm{1}}{\mathrm{10}},{b}=−\frac{\mathrm{3}}{\mathrm{10}} \\ $$$${f}=−\frac{{e}^{{t}} \left({cos}\left({t}\right)+\mathrm{3}{sin}\left({t}\right)\right)}{\mathrm{10}} \\ $$$${general}\:{solution}\:{ae}^{{t}} +{be}^{\mathrm{4}{t}} −\frac{{e}^{{t}} \left({cos}\left({t}\right)+\mathrm{3}{sin}\left({t}\right)\right)}{\mathrm{10}} \\ $$
