Question Number 42621 by maxmathsup by imad last updated on 29/Aug/18

$${find}\:\int\:{th}\left({x}\right){dx}\: \\ $$
Commented by maxmathsup by imad last updated on 30/Aug/18
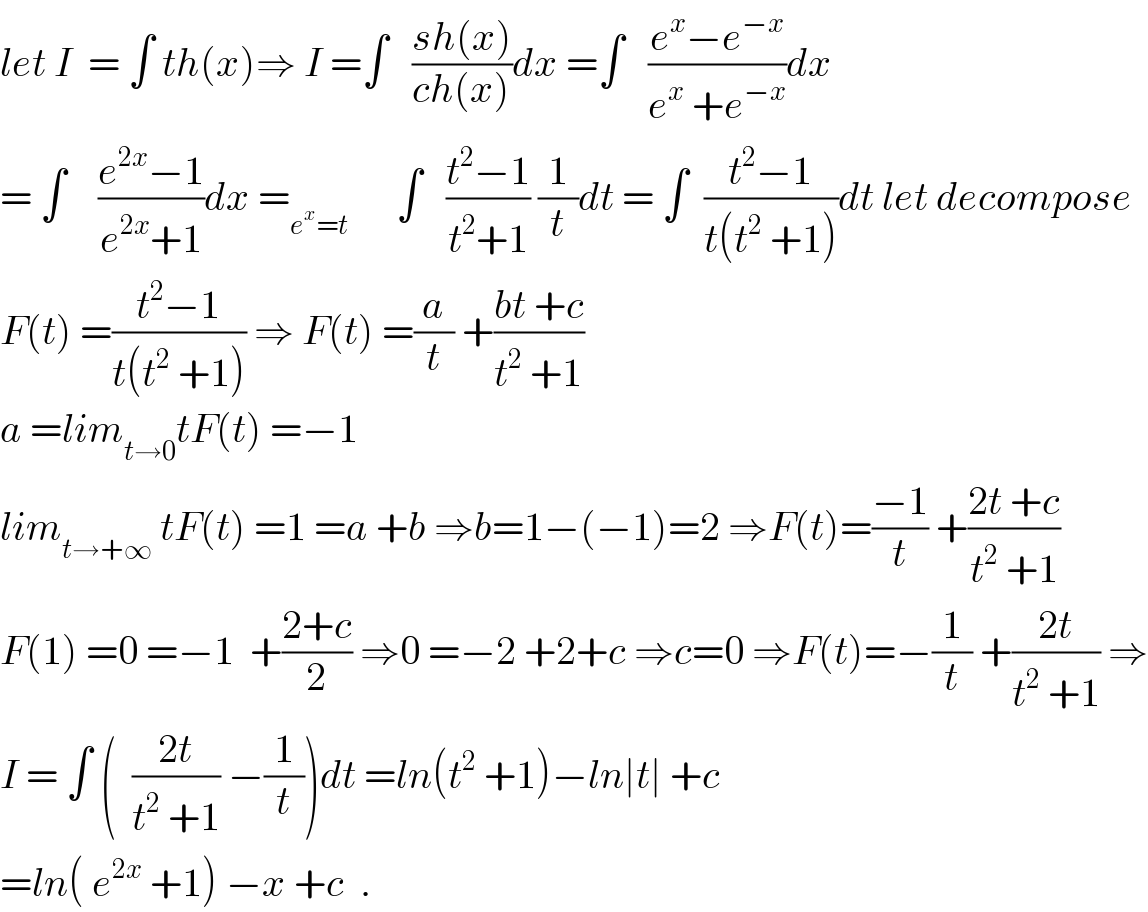
$${let}\:{I}\:\:=\:\int\:{th}\left({x}\right)\Rightarrow\:{I}\:=\int\:\:\:\frac{{sh}\left({x}\right)}{{ch}\left({x}\right)}{dx}\:=\int\:\:\:\frac{{e}^{{x}} −{e}^{−{x}} }{{e}^{{x}} \:+{e}^{−{x}} }{dx} \\ $$$$=\:\int\:\:\:\:\frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{{e}^{\mathrm{2}{x}} +\mathrm{1}}{dx}\:=_{{e}^{{x}} ={t}} \:\:\:\:\:\:\int\:\:\:\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\:\frac{\mathrm{1}}{{t}}{dt}\:=\:\int\:\:\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}{dt}\:{let}\:{decompose} \\ $$$${F}\left({t}\right)\:=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow\:{F}\left({t}\right)\:=\frac{{a}}{{t}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow\mathrm{0}} {tF}\left({t}\right)\:=−\mathrm{1} \\ $$$${lim}_{{t}\rightarrow+\infty} \:{tF}\left({t}\right)\:=\mathrm{1}\:={a}\:+{b}\:\Rightarrow{b}=\mathrm{1}−\left(−\mathrm{1}\right)=\mathrm{2}\:\Rightarrow{F}\left({t}\right)=\frac{−\mathrm{1}}{{t}}\:+\frac{\mathrm{2}{t}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)\:=\mathrm{0}\:=−\mathrm{1}\:\:+\frac{\mathrm{2}+{c}}{\mathrm{2}}\:\Rightarrow\mathrm{0}\:=−\mathrm{2}\:+\mathrm{2}+{c}\:\Rightarrow{c}=\mathrm{0}\:\Rightarrow{F}\left({t}\right)=−\frac{\mathrm{1}}{{t}}\:+\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${I}\:=\:\int\:\left(\:\:\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:−\frac{\mathrm{1}}{{t}}\right){dt}\:={ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)−{ln}\mid{t}\mid\:+{c} \\ $$$$={ln}\left(\:{e}^{\mathrm{2}{x}} \:+\mathrm{1}\right)\:−{x}\:+{c}\:\:. \\ $$
