Menu Close

find-the-3-rd-derivative-of-x-5-ln-2x-using-the-Leibniz-theorem-

Tinku Tara 0 Comments
Pin




Question Number 83189 by john santu last updated on 28/Feb/20
find the 3^(rd) derivative of x^5 ln(2x) using the Leibniz theorem
$$\mathrm{find}\:\mathrm{the}\:\mathrm{3}\:^{\mathrm{rd}} \:\mathrm{derivative}\:\mathrm{of}\: \\ $$$$\mathrm{x}^{\mathrm{5}} \:\mathrm{ln}\left(\mathrm{2x}\right)\:\mathrm{using}\:\mathrm{the}\:\mathrm{Leibniz}\:\mathrm{theorem} \\ $$
Commented by jagoll last updated on 28/Feb/20
y = x^5 ln(2x) y ′(x) = 5x^4 ln(2x) + ((2x^5 )/(2x)) y′(x) = 5x^4 ln(2x)+ x^4 y′′(x)= 20x^3 ln(2x)+ ((10x^4 )/(2x))+4x^3 y′′ (x) = 20x^3 ln(2x) + 9x^3 y′′′(x) = 60x^2 ln(2x) + ((40x^3 )/(2x))+27x^2 y′′′(x) = 60x^2 ln(2x) + 47x^2
$$\mathrm{y}\:=\:\mathrm{x}^{\mathrm{5}} \:\mathrm{ln}\left(\mathrm{2x}\right) \\ $$$$\mathrm{y}\:'\left(\mathrm{x}\right)\:=\:\mathrm{5x}^{\mathrm{4}} \:\mathrm{ln}\left(\mathrm{2x}\right)\:+\:\frac{\mathrm{2x}^{\mathrm{5}} }{\mathrm{2x}} \\ $$$$\mathrm{y}'\left(\mathrm{x}\right)\:=\:\mathrm{5x}^{\mathrm{4}} \:\mathrm{ln}\left(\mathrm{2x}\right)+\:\mathrm{x}^{\mathrm{4}} \\ $$$$\mathrm{y}''\left(\mathrm{x}\right)=\:\mathrm{20x}^{\mathrm{3}} \:\mathrm{ln}\left(\mathrm{2x}\right)+\:\frac{\mathrm{10x}^{\mathrm{4}} }{\mathrm{2x}}+\mathrm{4x}^{\mathrm{3}} \\ $$$$\mathrm{y}''\:\left(\mathrm{x}\right)\:=\:\mathrm{20x}^{\mathrm{3}} \:\mathrm{ln}\left(\mathrm{2x}\right)\:+\:\mathrm{9x}^{\mathrm{3}} \\ $$$$\mathrm{y}'''\left(\mathrm{x}\right)\:=\:\mathrm{60x}^{\mathrm{2}} \:\mathrm{ln}\left(\mathrm{2x}\right)\:+\:\frac{\mathrm{40x}^{\mathrm{3}} }{\mathrm{2x}}+\mathrm{27x}^{\mathrm{2}} \\ $$$$\mathrm{y}'''\left(\mathrm{x}\right)\:=\:\mathrm{60x}^{\mathrm{2}} \:\mathrm{ln}\left(\mathrm{2x}\right)\:+\:\mathrm{47x}^{\mathrm{2}} \\ $$
Commented by mr W last updated on 28/Feb/20
(x^5 ln (2x))^((3)) =x^5 ((2/x^3 ))+3(5x^4 )(−(1/x^2 ))+3(20x^3 )((1/x))+(60x^2 )ln (2x) =2x^2 −15x^2 +60x^2 +60x^2 ln (2x) =x^2 (47+60 ln (2x))
$$\left({x}^{\mathrm{5}} \mathrm{ln}\:\left(\mathrm{2}{x}\right)\right)^{\left(\mathrm{3}\right)} \\ $$$$={x}^{\mathrm{5}} \left(\frac{\mathrm{2}}{{x}^{\mathrm{3}} }\right)+\mathrm{3}\left(\mathrm{5}{x}^{\mathrm{4}} \right)\left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)+\mathrm{3}\left(\mathrm{20}{x}^{\mathrm{3}} \right)\left(\frac{\mathrm{1}}{{x}}\right)+\left(\mathrm{60}{x}^{\mathrm{2}} \right)\mathrm{ln}\:\left(\mathrm{2}{x}\right) \\ $$$$=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{15}{x}^{\mathrm{2}} +\mathrm{60}{x}^{\mathrm{2}} +\mathrm{60}{x}^{\mathrm{2}} \:\mathrm{ln}\:\left(\mathrm{2}{x}\right) \\ $$$$={x}^{\mathrm{2}} \left(\mathrm{47}+\mathrm{60}\:\mathrm{ln}\:\left(\mathrm{2}{x}\right)\right) \\ $$
Commented by mathmax by abdo last updated on 28/Feb/20
direct calculus f(x)=x^5 ln(2x) ⇒ f^((1)) (x)=5x^4 ln(2x) +x^5 ×(1/x) =5x^4 ln(2x)+x^4 f^((2)) (x)=20x^3 ln(2x)+5x^4 ×(1/x) +4x^3 =20x^3 ln(2x)+5x^3 +4x^3 =20x^3 ln(2x)+9x^3 ⇒f^((3)) (x)=60x^2 ln(2x)+20x^3 ×(1/x) +27x^2 =60x^2 ln(2x) +47 x^2 =x^2 {60ln(2x)+47}
$${direct}\:{calculus}\:{f}\left({x}\right)={x}^{\mathrm{5}} {ln}\left(\mathrm{2}{x}\right)\:\Rightarrow \\ $$$${f}^{\left(\mathrm{1}\right)} \left({x}\right)=\mathrm{5}{x}^{\mathrm{4}} {ln}\left(\mathrm{2}{x}\right)\:+{x}^{\mathrm{5}} ×\frac{\mathrm{1}}{{x}}\:=\mathrm{5}{x}^{\mathrm{4}} {ln}\left(\mathrm{2}{x}\right)+{x}^{\mathrm{4}} \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{20}{x}^{\mathrm{3}} {ln}\left(\mathrm{2}{x}\right)+\mathrm{5}{x}^{\mathrm{4}} ×\frac{\mathrm{1}}{{x}}\:+\mathrm{4}{x}^{\mathrm{3}} \:=\mathrm{20}{x}^{\mathrm{3}} {ln}\left(\mathrm{2}{x}\right)+\mathrm{5}{x}^{\mathrm{3}} \:+\mathrm{4}{x}^{\mathrm{3}} \\ $$$$=\mathrm{20}{x}^{\mathrm{3}} {ln}\left(\mathrm{2}{x}\right)+\mathrm{9}{x}^{\mathrm{3}} \:\Rightarrow{f}^{\left(\mathrm{3}\right)} \left({x}\right)=\mathrm{60}{x}^{\mathrm{2}} {ln}\left(\mathrm{2}{x}\right)+\mathrm{20}{x}^{\mathrm{3}} ×\frac{\mathrm{1}}{{x}}\:+\mathrm{27}{x}^{\mathrm{2}} \\ $$$$=\mathrm{60}{x}^{\mathrm{2}} {ln}\left(\mathrm{2}{x}\right)\:+\mathrm{47}\:{x}^{\mathrm{2}} \:={x}^{\mathrm{2}} \left\{\mathrm{60}{ln}\left(\mathrm{2}{x}\right)+\mathrm{47}\right\} \\ $$
Commented by jagoll last updated on 28/Feb/20
what generally Leibniz theorem sir
$$\mathrm{what}\:\mathrm{generally}\:\mathrm{Leibniz}\:\mathrm{theorem}\:\mathrm{sir} \\ $$
Commented by jagoll last updated on 28/Feb/20
yes sir. thank you
$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathmax by abdo last updated on 29/Feb/20
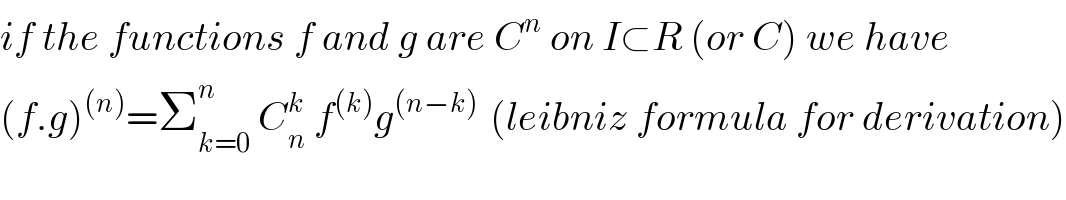
if the functions f and g are C^n on I⊂R (or C) we have (f.g)^((n)) =Σ_(k=0) ^n C_n ^k f^((k)) g^((n−k) ) (leibniz formula for derivation)
$${if}\:{the}\:{functions}\:{f}\:{and}\:{g}\:{are}\:{C}^{{n}} \:{on}\:{I}\subset{R}\:\left({or}\:{C}\right)\:{we}\:{have} \\ $$$$\left({f}.{g}\right)^{\left({n}\right)} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{f}^{\left({k}\right)} {g}^{\left({n}−{k}\right)\:} \:\left({leibniz}\:{formula}\:{for}\:{derivation}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *