Menu Close

Find-the-angle-between-the-curves-1-x-2-y-1-y-and-x-3-2-2y-2-x-2-y-2-a-2-2-and-x-2-y-2-a-2-

Tinku Tara 0 Comments
Pin




Question Number 58097 by rahul 19 last updated on 17/Apr/19
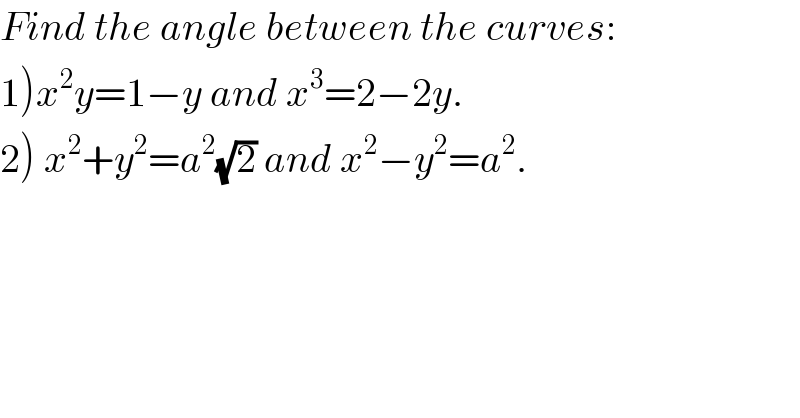
Find the angle between the curves: 1)x^2 y=1−y and x^3 =2−2y. 2) x^2 +y^2 =a^2 (√2) and x^2 −y^2 =a^2 .
$${Find}\:{the}\:{angle}\:{between}\:{the}\:{curves}: \\ $$$$\left.\mathrm{1}\right){x}^{\mathrm{2}} {y}=\mathrm{1}−{y}\:{and}\:{x}^{\mathrm{3}} =\mathrm{2}−\mathrm{2}{y}. \\ $$$$\left.\mathrm{2}\right)\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \sqrt{\mathrm{2}}\:{and}\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} ={a}^{\mathrm{2}} . \\ $$
Answered by tanmay last updated on 17/Apr/19
1)x^2 y=1−y y=(1/(1+x^2 )) x^3 =2−2y x^3 =2−2((1/(1+x^2 ))) x^3 (1+x^2 )=2(1+x^2 )−2 x^3 +x^5 =2x^2 x^2 (x+x^3 −2)=0 x^2 {(x−1)+x^3 −1}=0 x^2 (x−1)(1+x^2 +x+1)=0 x^2 (x−1)(x^2 +x+2)=0 x=0 x=1 x=((−1±(√(1−4×1×2)))/(2×1)) x=((−1±(√7) i)/2) ←not feasible first curve y=(1/(1+x^2 )) (dy/dx)=((−1)/((1+x^2 )^2 ))×2x m_1 =((−2×1)/((1+1)^2 ))=((−1)/2) 2y=2−x^3 y=1−(x^3 /2) →(dy/dx)=((−3)/2)×x^2 =((−3x^2 )/2) when point (x=1) m_2 =((−3)/2) [point x=1] tanθ_2 =((((−1)/2)+(3/2))/(1+(((−1)/2))(((−3)/2)))) =((2/2)/(1+(3/4)))=(4/7)→θ_2 =tan^(−1) ((4/7)) discussion... let two curve intesect at point(x_1 ,y_1 ) then angle between two tangents at that point(x_1 ,y_1 ) is the angle between two curves
$$\left.\mathrm{1}\right){x}^{\mathrm{2}} {y}=\mathrm{1}−{y} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{3}} =\mathrm{2}−\mathrm{2}{y} \\ $$$${x}^{\mathrm{3}} =\mathrm{2}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right) \\ $$$${x}^{\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)=\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2} \\ $$$${x}^{\mathrm{3}} +{x}^{\mathrm{5}} =\mathrm{2}{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \left({x}+{x}^{\mathrm{3}} −\mathrm{2}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left\{\left({x}−\mathrm{1}\right)+{x}^{\mathrm{3}} −\mathrm{1}\right\}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} +{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{2}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0} \\ $$$${x}=\mathrm{1} \\ $$$${x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}×\mathrm{1}×\mathrm{2}}}{\mathrm{2}×\mathrm{1}} \\ $$$${x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{7}}\:{i}}{\mathrm{2}}\:\leftarrow{not}\:{feasible} \\ $$$$ \\ $$$${first}\:{curve}\:{y}=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\frac{{dy}}{{dx}}=\frac{−\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }×\mathrm{2}{x}\: \\ $$$${m}_{\mathrm{1}} =\frac{−\mathrm{2}×\mathrm{1}}{\left(\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}{y}=\mathrm{2}−{x}^{\mathrm{3}} \\ $$$${y}=\mathrm{1}−\frac{{x}^{\mathrm{3}} }{\mathrm{2}}\:\:\rightarrow\frac{{dy}}{{dx}}=\frac{−\mathrm{3}}{\mathrm{2}}×{x}^{\mathrm{2}} =\frac{−\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${when}\:{point}\:\left({x}=\mathrm{1}\right) \\ $$$$ \\ $$$${m}_{\mathrm{2}} =\frac{−\mathrm{3}}{\mathrm{2}}\:\left[{point}\:{x}=\mathrm{1}\right] \\ $$$${tan}\theta_{\mathrm{2}} =\frac{\frac{−\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}}{\mathrm{1}+\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\left(\frac{−\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\:\:=\frac{\frac{\mathrm{2}}{\mathrm{2}}}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}}=\frac{\mathrm{4}}{\mathrm{7}}\rightarrow\theta_{\mathrm{2}} ={tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{7}}\right) \\ $$$${discussion}… \\ $$$${let}\:{two}\:{curve}\:{intesect}\:{at}\:{point}\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right) \\ $$$${then}\:{angle}\:{between}\:{two}\:{tangents}\:{at}\:{that} \\ $$$${point}\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)\:{is}\:{the}\:{angle}\:{between}\:{two}\:{curves} \\ $$
Commented by rahul 19 last updated on 17/Apr/19
Thank u sir!
$${Thank}\:{u}\:{sir}! \\ $$
Commented by tanmay last updated on 18/Apr/19
most welcome rahul...
$${most}\:{welcome}\:{rahul}… \\ $$
Answered by tanmay last updated on 17/Apr/19
2) x^2 +y^2 =a^2 (√2) x^2 −y^2 =a^2 2x^2 =a^2 (1+(√2) ) x^2 =((a^2 (1+(√2) ))/2)→x=a×(√(((√2) +1)/2)) y^2 =a^2 (√2) −((a^2 (1+(√2) ))/2) y^2 =((2(√2) a^2 −a^2 −(√2) a^2 )/2) y^2 =((a^2 ((√2) −1))/2)→y=a(√((((√2) −1)/2) )) first curve x^2 +y^2 =a^2 (√2) 2x+2y×(dy/dx)=0 (dy/dx)=((−x)/y)→((−1×(a×(√(((√2) +1)/2)) ))/(a×(√(((√2) −1)/2)))) m_1 =−1×(√(((√2) +1)/( (√2) −1))) =−1×((((√2) +1)/1)) second curve.. x^2 −y^2 =a^2 y^2 =x^2 −a^2 y^2 =a^2 (((1+(√2))/2))−a^2 y^2 =((a^2 ((√2) −1))/2) now x^2 −y^2 =a^2 2x−2y×(dy/dx)=0 (dy/dx)=(x/y)→m_2 =((a×(√(((√2) +1)/2)))/(a(√(((√2) −1)/2))))=(√2) +1 tanθ=((m_2 −m_1 )/(1+m_1 m_2 ))=((2((√2) +1))/(1+((√2) +1)×{−1((√(2 )) +1)})) tsnθ=((2((√2) +1))/(1−(3+2(√2) )))=((2((√2) +1))/(1−3−2(√2)))=((2((√2) +1))/(−2(1+(√2) )))=−1 tanθ=−1=tan135^o θ=135^o
$$\left.\mathrm{2}\right)\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} ={a}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right) \\ $$$${x}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right)}{\mathrm{2}}\rightarrow{x}={a}×\sqrt{\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\mathrm{2}}} \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} \sqrt{\mathrm{2}}\:−\frac{{a}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right)}{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{2}\sqrt{\mathrm{2}}\:{a}^{\mathrm{2}} −{a}^{\mathrm{2}} −\sqrt{\mathrm{2}}\:{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} \left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)}{\mathrm{2}}\rightarrow{y}={a}\sqrt{\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\mathrm{2}}\:} \\ $$$${first}\:{curve} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \sqrt{\mathrm{2}}\: \\ $$$$\mathrm{2}{x}+\mathrm{2}{y}×\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=\frac{−{x}}{{y}}\rightarrow\frac{−\mathrm{1}×\left({a}×\sqrt{\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\mathrm{2}}}\:\right)}{{a}×\sqrt{\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\mathrm{2}}}} \\ $$$${m}_{\mathrm{1}} =−\mathrm{1}×\sqrt{\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\:\sqrt{\mathrm{2}}\:−\mathrm{1}}}\:=−\mathrm{1}×\left(\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\mathrm{1}}\right) \\ $$$${second}\:{curve}.. \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} ={x}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}\right)−{a}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} \left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)}{\mathrm{2}} \\ $$$${now}\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}−\mathrm{2}{y}×\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=\frac{{x}}{{y}}\rightarrow{m}_{\mathrm{2}} =\frac{{a}×\sqrt{\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\mathrm{2}}}}{{a}\sqrt{\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\mathrm{2}}}}=\sqrt{\mathrm{2}}\:+\mathrm{1} \\ $$$${tan}\theta=\frac{{m}_{\mathrm{2}} −{m}_{\mathrm{1}} }{\mathrm{1}+{m}_{\mathrm{1}} {m}_{\mathrm{2}} }=\frac{\mathrm{2}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)}{\mathrm{1}+\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)×\left\{−\mathrm{1}\left(\sqrt{\mathrm{2}\:}\:+\mathrm{1}\right)\right\}} \\ $$$${tsn}\theta=\frac{\mathrm{2}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)}{\mathrm{1}−\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\right)}=\frac{\mathrm{2}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)}{\mathrm{1}−\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\mathrm{2}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)}{−\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right)}=−\mathrm{1} \\ $$$${tan}\theta=−\mathrm{1}={tan}\mathrm{135}^{{o}} \\ $$$$\theta=\mathrm{135}^{{o}} \\ $$$$ \\ $$
Commented by rahul 19 last updated on 17/Apr/19
Ans given is 45°.
Commented by MJS last updated on 17/Apr/19
without going through above workings: the angle between 2 curves = the angle between their tangents. the angle between 2 straight lines is not unique, it′s either α or 180°−α ⇒ 45° is ok and 135° is ok too
$$\mathrm{without}\:\mathrm{going}\:\mathrm{through}\:\mathrm{above}\:\mathrm{workings}: \\ $$$$\mathrm{the}\:\mathrm{angle}\:\mathrm{between}\:\mathrm{2}\:\mathrm{curves}\:=\:\mathrm{the}\:\mathrm{angle} \\ $$$$\mathrm{between}\:\mathrm{their}\:\mathrm{tangents}.\:\mathrm{the}\:\mathrm{angle}\:\mathrm{between} \\ $$$$\mathrm{2}\:\mathrm{straight}\:\mathrm{lines}\:\mathrm{is}\:\mathrm{not}\:\mathrm{unique},\:\mathrm{it}'\mathrm{s}\:\mathrm{either} \\ $$$$\alpha\:\mathrm{or}\:\mathrm{180}°−\alpha\:\Rightarrow\:\mathrm{45}°\:\mathrm{is}\:\mathrm{ok}\:\mathrm{and}\:\mathrm{135}°\:\mathrm{is}\:\mathrm{ok}\:\mathrm{too} \\ $$
Commented by tanmay last updated on 18/Apr/19
thank you sir...
$${thank}\:{you}\:{sir}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *