Find-the-area-between-the-circle-2acos-and-cardiode-a-1-cos-

Question Number 113868 by Ar Brandon last updated on 15/Sep/20

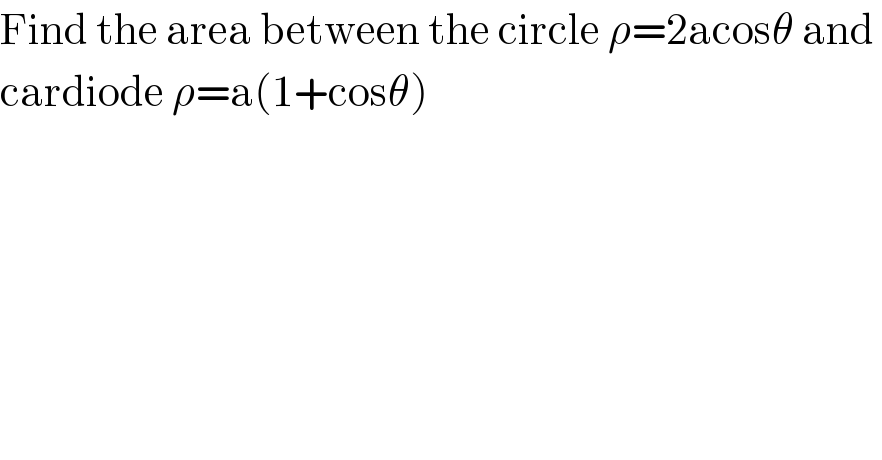
Find the area between the circle ρ = 2 acos θ and

cardiode ρ = a (1 + \cos θ)

Commented by kaivan.ahmadi last updated on 18/Sep/20

2 a c o s θ = a + a c o s θ \Rightarrow a c o s θ = a \Rightarrow c o s θ = 1 \Rightarrow

θ = 0, θ = 2 π

\int_{0}^{2 π} ({(2 a c o s θ)}^{2} - {(a (1 + c o s θ))}^{2}) d θ =

\int_{0}^{2 π} (4 a^{2} {c o s}^{2} θ - a^{2} {c o s}^{2} θ - 2 a^{2} c o s θ - a^{2}) d θ =

a^{2} \int_{0}^{2 π} (3 {c o s}^{2} θ - 2 c o s θ - 1) d θ =

a^{2} (\frac{3 θ}{2} - \frac{3 s i n 2 θ}{4} - 2 s i n θ - θ ∣_{0}^{2 π}) =

a^{2} [(3 π - 0 - 0 - 2 π) - (0 - 0 - 0 - 0)] =

a^{2} π