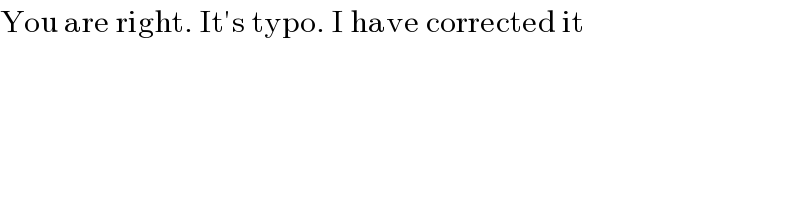Question Number 32775 by NECx last updated on 02/Apr/18
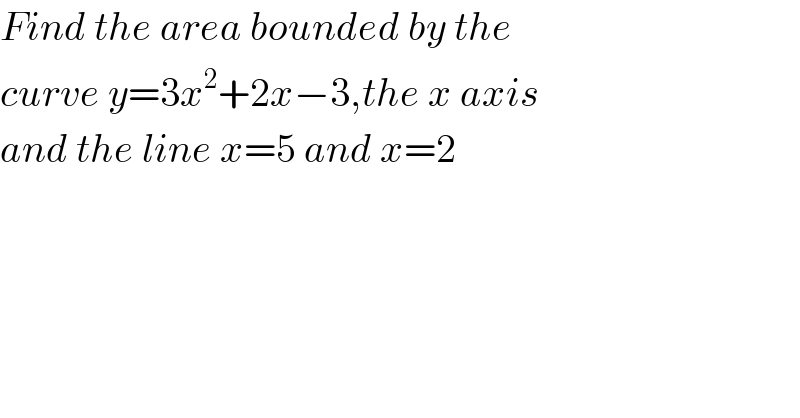
Answered by MJS last updated on 02/Apr/18
![1. check the zeros x^2 +(2/3)x−1=0 x=−(1/3)±(√((1/9)+1))=−(1/3)±((√(10))/3) x_1 ≈−1.39 and x_2 ≈.72 are both inside [−5;2]⇒changes of sign 2. area: x<x_1 ⇒f(x)>0 x∈]x_1 ;x_2 [⇒f(x)<0 x>x_2 ⇒f(x)>0 ∫_(−5) ^x_1 f(x)dx−∫_x_1 ^x_2 f(x)dx+∫_x_2 ^2 f(x)dx= =F(x)∣_(−5) ^x_1 −F(x)∣_x_1 ^x_2 +F(x)∣_x_2 ^2 = [F(x)=x^3 +x^2 −3x] =91+((80(√(10)))/(27))](https://www.tinkutara.com/question/Q32779.png)
Commented by MJS last updated on 02/Apr/18
Commented by NECx last updated on 02/Apr/18
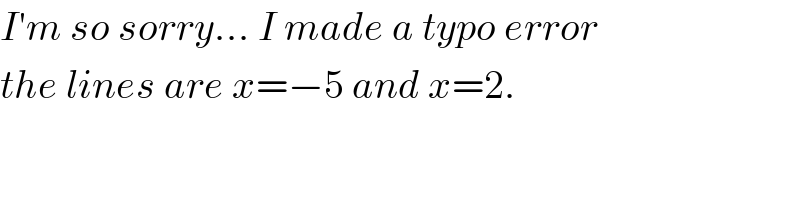
Commented by Joel578 last updated on 03/Apr/18
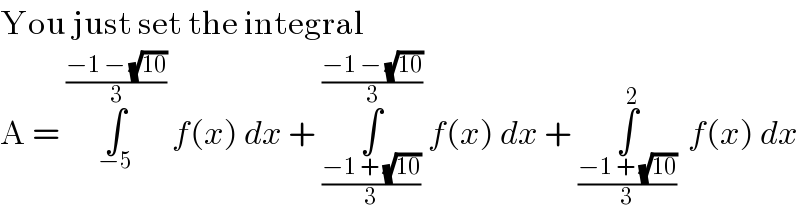
Commented by MJS last updated on 02/Apr/18
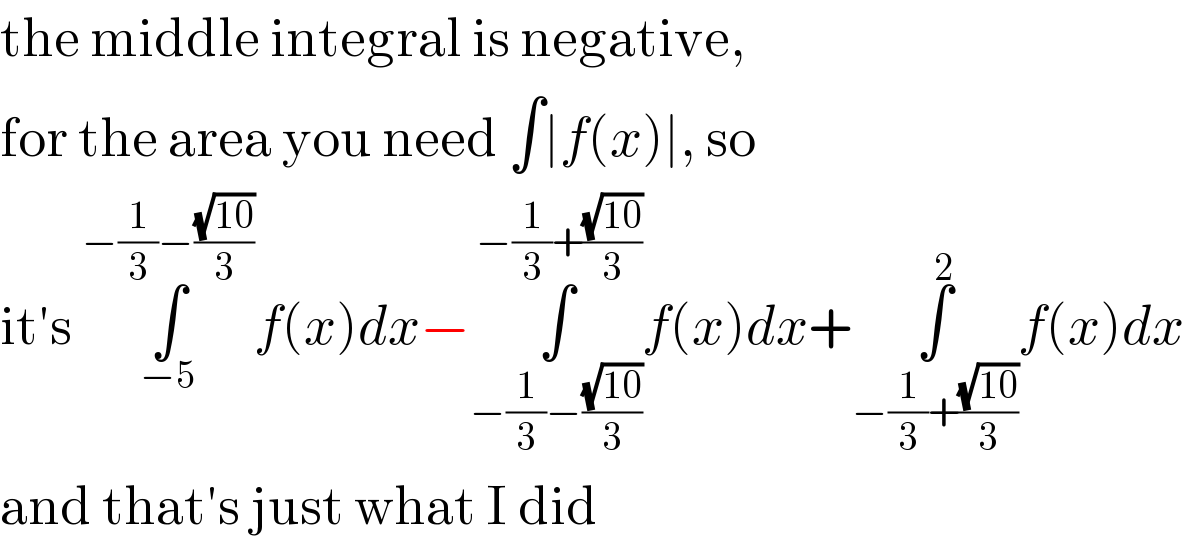
Commented by Joel578 last updated on 03/Apr/18