Question Number 61986 by necx1 last updated on 13/Jun/19
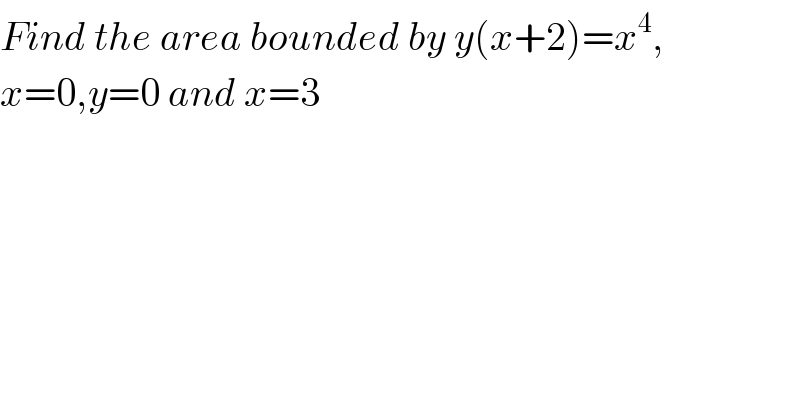
$${Find}\:{the}\:{area}\:{bounded}\:{by}\:{y}\left({x}+\mathrm{2}\right)={x}^{\mathrm{4}} , \\ $$$${x}=\mathrm{0},{y}=\mathrm{0}\:{and}\:{x}=\mathrm{3} \\ $$
Answered by mr W last updated on 13/Jun/19
![y=(x^4 /(x+2)) A=∫_0 ^3 (x^4 /(x+2)) dx A=∫_0 ^3 (((x+2)(x−2)(x^2 +4)+16)/(x+2)) dx A=∫_0 ^3 [(x−2)(x^2 +4)+((16)/(x+2))] dx A=∫_0 ^3 [x^3 −2x^2 +4x−8+((16)/(x+2))] dx A=[(1/4)x^4 −(2/3)x^3 +2x^2 −8x+16 ln (x+2)]_0 ^3 A=[(1/4)3^4 −(2/3)3^3 +2×3^2 −8×3+16 ln ((3+2)/2)] A=[−((15)/4)+16 ln (5/2)]=10.91](https://www.tinkutara.com/question/Q61987.png)
$${y}=\frac{{x}^{\mathrm{4}} }{{x}+\mathrm{2}} \\ $$$${A}=\int_{\mathrm{0}} ^{\mathrm{3}} \frac{{x}^{\mathrm{4}} }{{x}+\mathrm{2}}\:{dx} \\ $$$${A}=\int_{\mathrm{0}} ^{\mathrm{3}} \frac{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)+\mathrm{16}}{{x}+\mathrm{2}}\:{dx} \\ $$$${A}=\int_{\mathrm{0}} ^{\mathrm{3}} \left[\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)+\frac{\mathrm{16}}{{x}+\mathrm{2}}\right]\:{dx} \\ $$$${A}=\int_{\mathrm{0}} ^{\mathrm{3}} \left[{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{8}+\frac{\mathrm{16}}{{x}+\mathrm{2}}\right]\:{dx} \\ $$$${A}=\left[\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} −\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{16}\:\mathrm{ln}\:\left({x}+\mathrm{2}\right)\right]_{\mathrm{0}} ^{\mathrm{3}} \\ $$$${A}=\left[\frac{\mathrm{1}}{\mathrm{4}}\mathrm{3}^{\mathrm{4}} −\frac{\mathrm{2}}{\mathrm{3}}\mathrm{3}^{\mathrm{3}} +\mathrm{2}×\mathrm{3}^{\mathrm{2}} −\mathrm{8}×\mathrm{3}+\mathrm{16}\:\mathrm{ln}\:\frac{\mathrm{3}+\mathrm{2}}{\mathrm{2}}\right] \\ $$$${A}=\left[−\frac{\mathrm{15}}{\mathrm{4}}+\mathrm{16}\:\mathrm{ln}\:\frac{\mathrm{5}}{\mathrm{2}}\right]=\mathrm{10}.\mathrm{91} \\ $$
Commented by necx1 last updated on 13/Jun/19
$${Thank}\:{you}\:{so}\:{much}. \\ $$
