find-the-area-bounded-inner-the-curve-r-4-2cos-and-outer-the-curve-r-6-2cos-

Question Number 102369 by bobhans last updated on 08/Jul/20

f i n d t h e a r e a b o u n d e d i n n e r t h e c u r v e

r = 4 - 2 \cos θ a n d o u t e r t h e c u r v e r = 6 + 2 \cos θ

Answered by Ar Brandon last updated on 08/Jul/20

Area, A = \int_{0}^{2 π} \int_{4 - 2 \cos θ}^{6 + 2 \cos θ} rdrd θ = \int_{0}^{2 π} {[\frac{r^{2}}{2}]}_{4 - 2 \cos θ}^{6 + 2 \cos θ} d θ

\Rightarrow A = \frac{1}{2} \int_{0}^{2 π} {{(6 + 2 \cos θ)}^{2} - {(4 - 2 \cos θ)}^{2}} d θ

= \frac{1}{2} \int_{0}^{2 π} {(36 + 24 \cos θ + {4 \cos}^{2} θ) - (16 - 16 \cos θ + {4 \cos}^{2} θ)} d θ

= \frac{1}{2} \int_{0}^{2 π} (20 + 40 \cos θ) d θ = {[\frac{20 θ + 40 \sin θ}{2}]}_{0}^{2 π}

= 20 π square units

{D o n}^{'} t r e a l l y k n o w i f I^{'} v e d o n e i t i n t h e r i g h t w a y .

P l e a s e l e t m e k n o w w h a t y o u t h i n k .

Commented by mr W last updated on 09/Jul/20

y o u a r e r i g h t . i m i s r e a d, b e c a u s e t h i s

i s h o w t h e q u e s t i o n i s d i s p l a y e d o n

m y d e v i c e :

Commented by mr W last updated on 08/Jul/20

A = \int_{0}^{2 π} \int_{4 - 2 \cos θ}^{6} rdrd θ

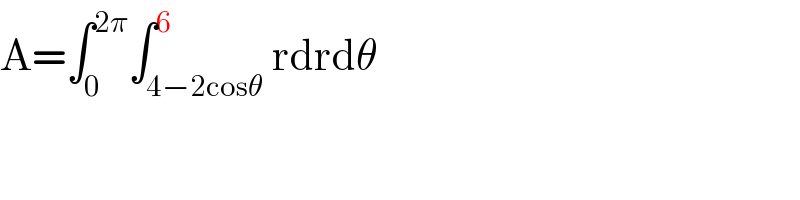
Commented by Ar Brandon last updated on 08/Jul/20

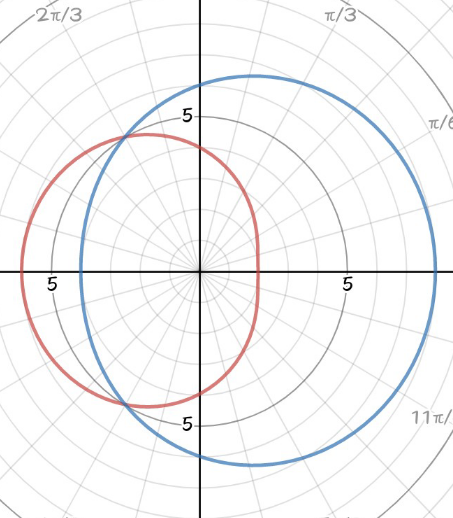
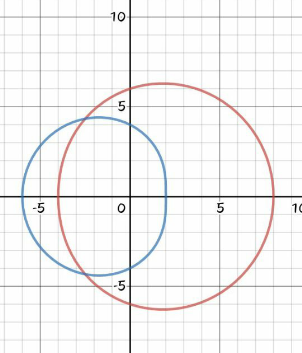
Why the 6 at the upper bound, mr W ?

Commented by mr W last updated on 09/Jul/20

Commented by mr W last updated on 09/Jul/20

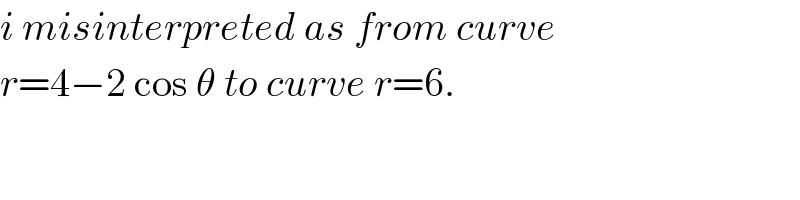
i m i s i n t e r p r e t e d a s f r o m c u r v e

r = 4 - 2 \cos θ t o c u r v e r = 6 .

Commented by bobhans last updated on 09/Jul/20

s i r w h y \underset{0}{\int^{2 π}} ? i t h i n k \underset{0}{\int^{π}} ?

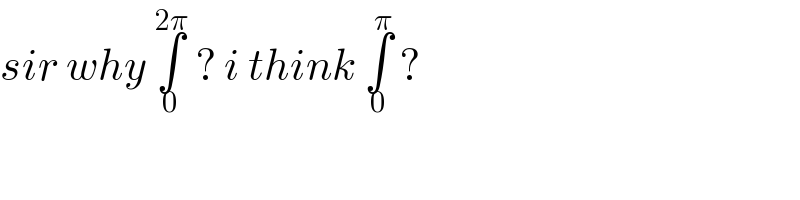
Commented by bobhans last updated on 09/Jul/20

Commented by Ar Brandon last updated on 09/Jul/20

OK Sir

Commented by Ar Brandon last updated on 09/Jul/20

{You}^{'} re heading somewhere mr Bobhans . I think {you}^{'} re

making a point there . {Let}^{'} s see;

Mathematically inner the curve 4 - 2 \cos θ implies

4 - 2 \cos θ < r

and outer the curve 6 + 2 \cos θ implies

6 + 2 \cos θ > r

Therefore at points of intersection r = r

\Rightarrow 4 - 2 \cos θ = 6 + 2 \cos θ \Rightarrow \cos θ = \frac{- 1}{2}

\Rightarrow θ_{1} = \frac{4}{3} π, θ_{2} = \frac{2}{3} π

Commented by Ar Brandon last updated on 09/Jul/20

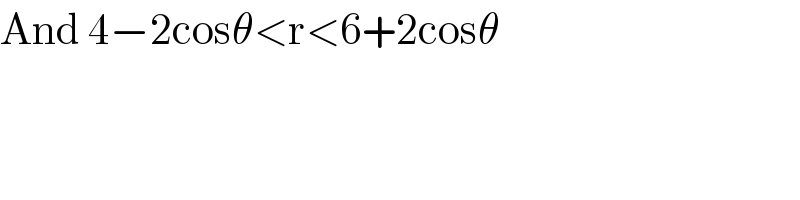
And 4 - 2 \cos θ < r < 6 + 2 \cos θ

Commented by bemath last updated on 09/Jul/20

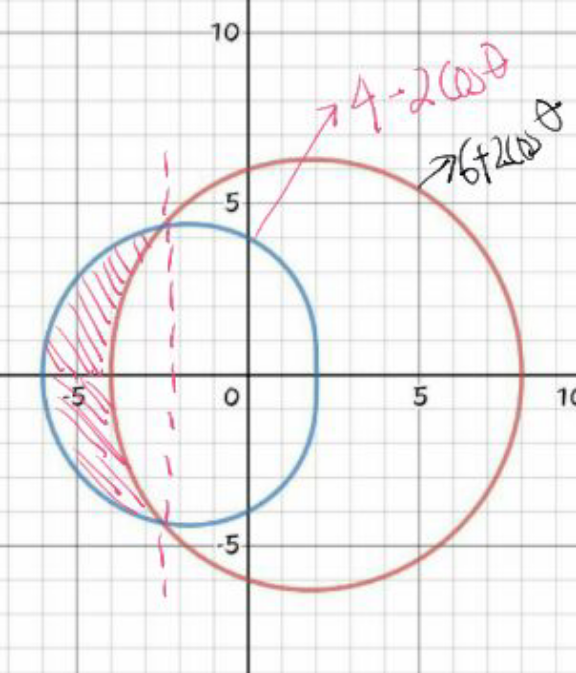
Commented by 1549442205 last updated on 09/Jul/20

If the figure is bounded by

{\begin{cases} r = 4 - 2 \cos θ \\ r = 6 \end{cases} then

S = \int_{0}^{π} [6^{2} - {(4 - 2 \cos θ)}^{2}] d θ

= \int_{0}^{π} (20 + 16 \cos θ - {4 \cos}^{2} θ) d θ

= (20 θ + 16 \sin θ) ∣_{0}^{π} - 2 \int_{0}^{π} (1 + \cos 2 θ) d θ

= 20 π - (2 θ + \sin 2 θ) ∣_{0}^{π} = 18 π

If the figure is bounded {\begin{cases} r = 4 - 2 \cos θ \\ r = 6 + 2 \cos θ \end{cases} then

S = \int_{0}^{\frac{2 π}{3}} [{(6 + 2 \cos θ)}^{2} - {(4 - 2 \cos θ)}^{2}] d θ

= \int_{0}^{\frac{2 π}{3}} (20 + 40 \cos θ d θ = (20 θ + 40 \sin θ) ∣_{0}^{\frac{2 π}{3}}

= 20 \times \frac{2 π}{3} + 40 \times \frac{\sqrt{3}}{2} = \frac{40 π}{3} - 20 \sqrt{3} \approx 76.53

Commented by 1549442205 last updated on 09/Jul/20

Answered by Ar Brandon last updated on 09/Jul/20

Area, A = \int_{\frac{2 π}{3}}^{\frac{4 π}{3}} \int_{4 - 2 \cos θ}^{6 + 2 \cos θ} rdrd θ = \int_{\frac{2 π}{3}}^{\frac{4 π}{3}} {[\frac{r^{2}}{2}]}_{4 - 2 \cos θ}^{6 + 2 \cos θ} d θ

\Rightarrow A = \frac{1}{2} \int_{\frac{2 π}{3}}^{\frac{4 π}{3}} {{(6 + 2 \cos θ)}^{2} - {(4 - 2 \cos θ)}^{2}} d θ

= \frac{1}{2} \int_{\frac{2 π}{3}}^{\frac{4 π}{3}} {(36 + 24 \cos θ + {4 \cos}^{2} θ) - (16 - 16 \cos θ + {4 \cos}^{2} θ)} d θ

= \frac{1}{2} \int_{\frac{2 π}{3}}^{\frac{4 π}{3}} (20 + 40 \cos θ) d θ = {[\frac{20 θ + 40 \sin θ}{2}]}_{\frac{2 π}{3}}^{\frac{4 π}{3}}

= \frac{1}{2} [20 \times \frac{4 π}{3} - 40 \times \frac{\sqrt{3}}{2} - 20 \times \frac{2 π}{3} + 40 \times \frac{\sqrt{3}}{2}]

= \frac{20}{3} π square units

Answered by bemath last updated on 09/Jul/20

Facebook Tweet Pin