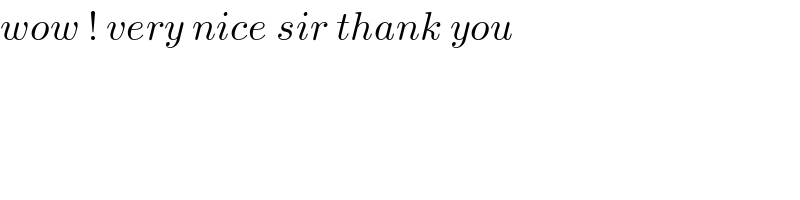find-the-area-bounded-the-parabola-y-4x-2-and-y-8-4x-2-by-using-intigral-help-me-

Question Number 101319 by mhmd last updated on 01/Jul/20

f i n d t h e a r e a b o u n d e d t h e p a r a b o l a

y = 4 x^{2} a n d y = 8 - 4 x^{2} ? b y u s i n g i n t i g r a l ?

h e l p m e

Commented by smridha last updated on 01/Jul/20

\boldsymbol t h e \boldsymbol a r e a \boldsymbol u n d e r \boldsymbol t h e \boldsymbol c u r v e s (\boldsymbol h e r e \boldsymbol p a r a b o l a)

\boldsymbol A = 2 [\int_{0}^{1} (8 - 4 \boldsymbol x^{2}) \boldsymbol d x - \int_{0}^{1} 4 \boldsymbol x^{2} \boldsymbol d x]

= 2 {[8 \boldsymbol x - \frac{8}{3} \boldsymbol x^{3}]}_{0}^{1} = 2 [\frac{8}{1} - \frac{8}{3}] = \frac{32}{3} .

Commented by mhmd last updated on 01/Jul/20

v e r y t h a n k s i r

Commented by smridha last updated on 01/Jul/20

welcome...I think you can draw the picture..

Commented by mhmd last updated on 01/Jul/20

y e s s i r

Answered by bobhans last updated on 01/Jul/20

intercept : {4 x}^{2} = 8 - {4 x}^{2}; {8 x}^{2} = 8; x = \pm 1

test x = \frac{1}{2} \to {\begin{cases} y = 4 \times \frac{1}{4} = 1 \\ y = 8 - 4 \times \frac{1}{4} = 7 \end{cases}

8 - {4 x}^{2} ⩾ {4 x}^{2}, so the area =

2 \underset{0}{\int^{1}} (8 - {8 x}^{2}) dx = 2 {[(8 x - \frac{8}{3} x^{3})]}_{0}^{1}

= 2 (8 - \frac{8}{3}) = 2 \times \frac{16}{3} = \frac{32}{3} ★

Commented by bramlex last updated on 02/Jul/20

♠ ★

♠ ★

Commented by mhmd last updated on 02/Jul/20

w o w! v e r y n i c e s i r t h a n k y o u

w o w! v e r y n i c e s i r t h a n k y o u

Facebook Tweet Pin