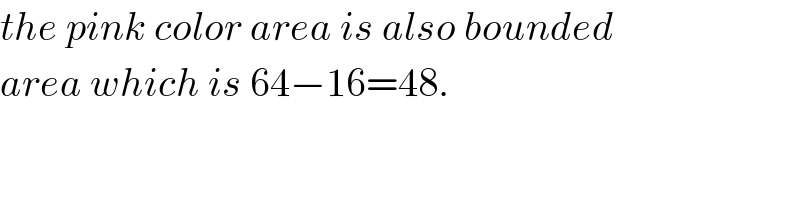Question Number 38568 by ajfour last updated on 27/Jun/18
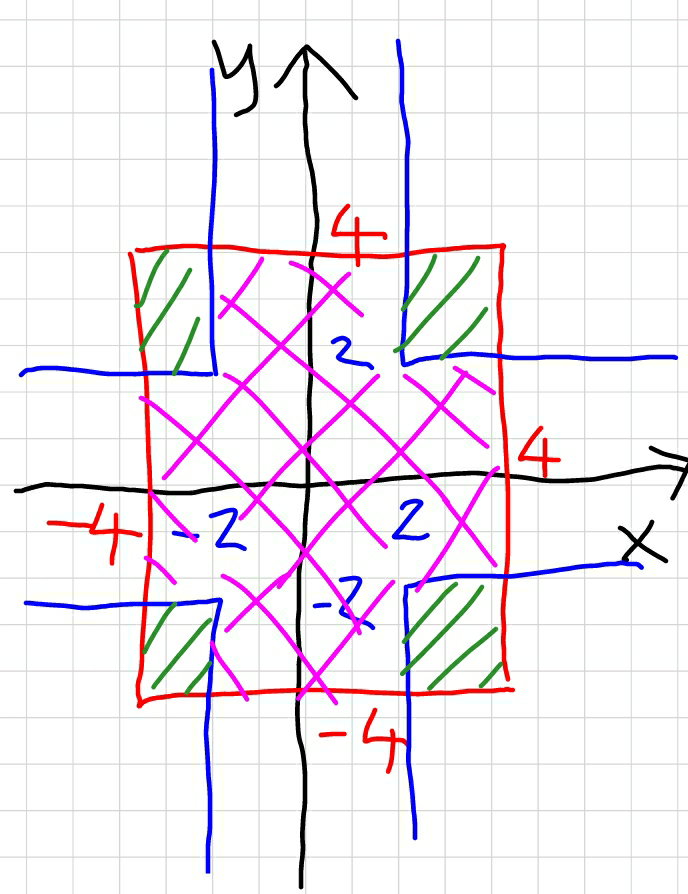
![Find the area common to min{[x], [y] } =2 and max{[x], [y] } =4 . [x] denotes the greatest integer less than or equal to x.](https://www.tinkutara.com/question/Q38568.png)
Commented by ajfour last updated on 27/Jun/18

Commented by MrW3 last updated on 27/Jun/18
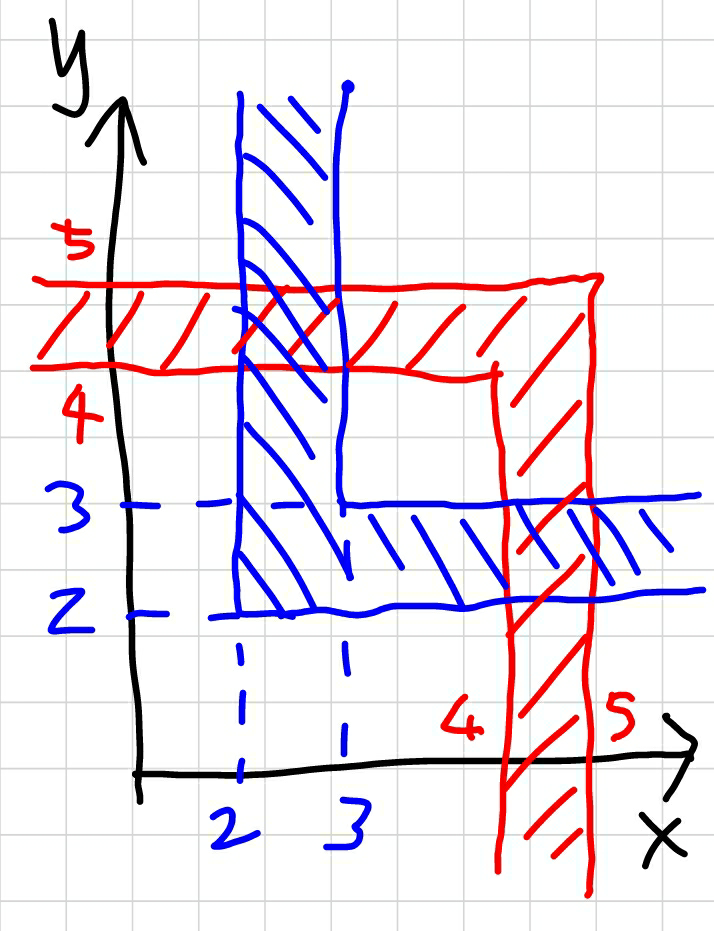
Commented by MrW3 last updated on 27/Jun/18

Commented by tanmay.chaudhury50@gmail.com last updated on 27/Jun/18
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Jun/18
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Jun/18
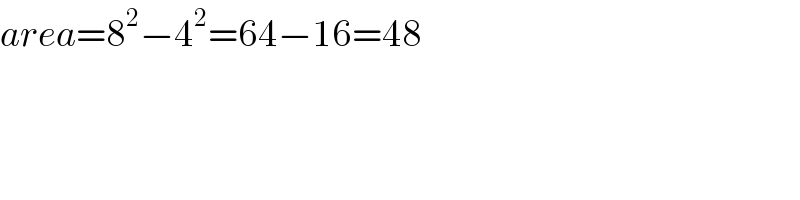
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Jun/18
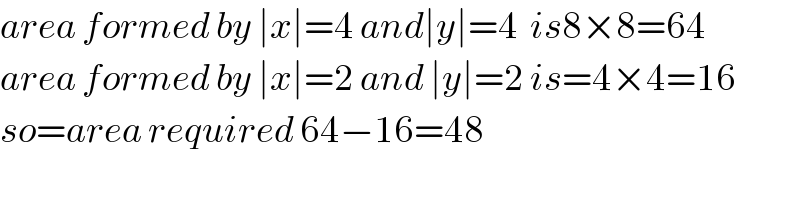
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Jun/18
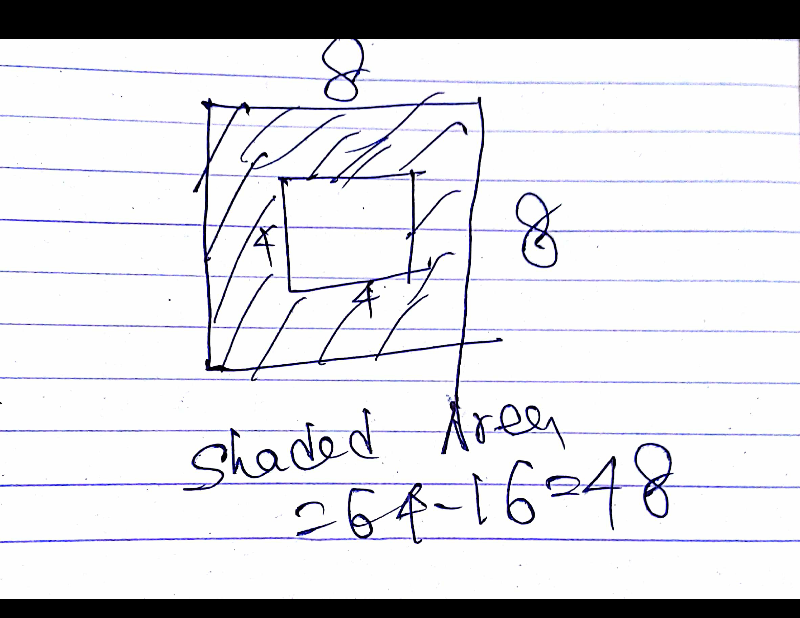
Commented by ajfour last updated on 27/Jun/18
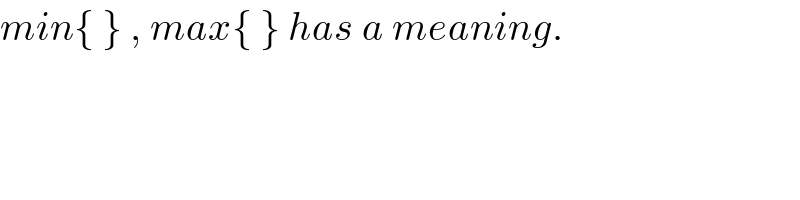
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Jun/18
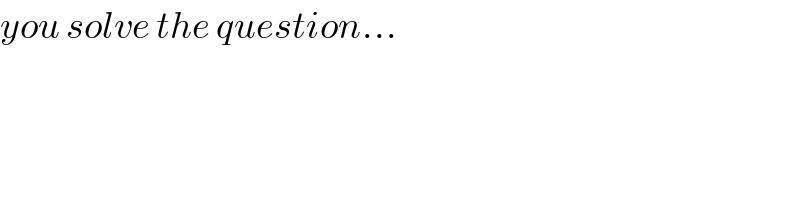
Commented by MrW3 last updated on 27/Jun/18
![area bounded by min{[x],[y]}=2 max{[x],[y]}=4 is 8. area bounded by min{∣x∣,∣y∣}=2 max{∣x∣,∣y∣}=4 is 16.](https://www.tinkutara.com/question/Q38619.png)
Commented by ajfour last updated on 27/Jun/18
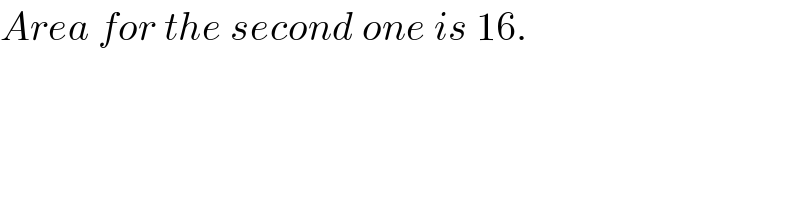
Commented by MrW3 last updated on 27/Jun/18

Commented by MrW3 last updated on 27/Jun/18
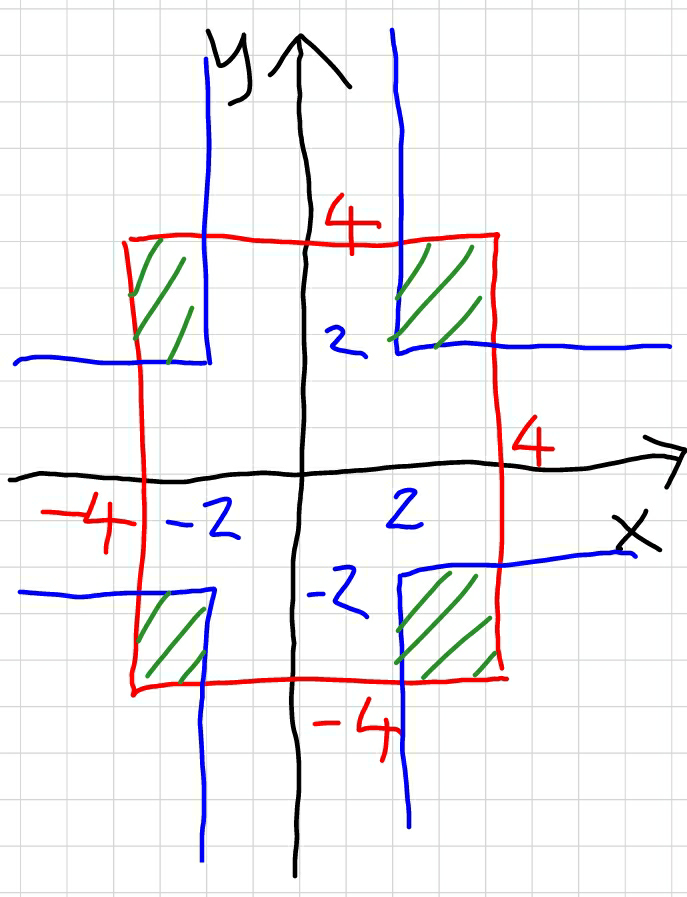
Commented by ajfour last updated on 27/Jun/18
Commented by ajfour last updated on 28/Jun/18

Commented by MrW3 last updated on 28/Jun/18
Commented by MrW3 last updated on 28/Jun/18