Question Number 90557 by I want to learn more last updated on 24/Apr/20
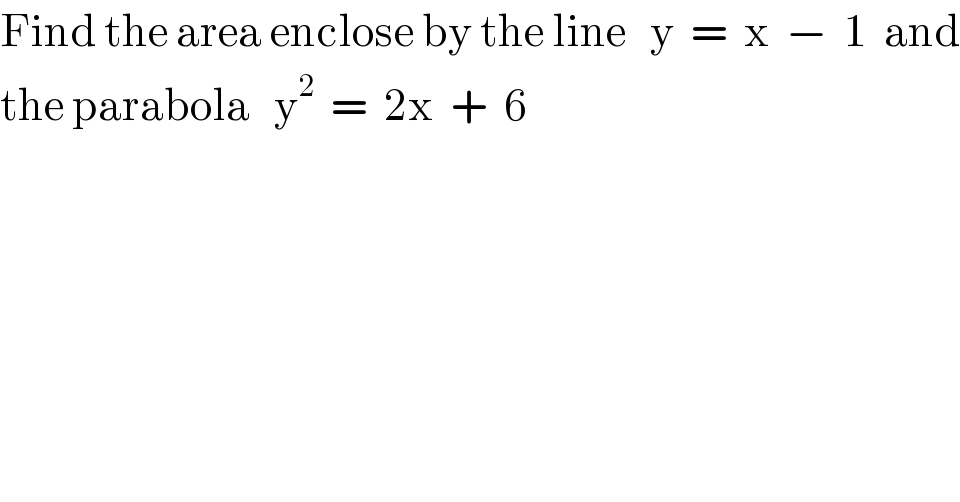
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{enclose}\:\mathrm{by}\:\mathrm{the}\:\mathrm{line}\:\:\:\mathrm{y}\:\:=\:\:\mathrm{x}\:\:−\:\:\mathrm{1}\:\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{parabola}\:\:\:\mathrm{y}^{\mathrm{2}} \:\:=\:\:\mathrm{2x}\:\:+\:\:\mathrm{6} \\ $$
Commented by I want to learn more last updated on 24/Apr/20

$$\mathrm{I}\:\mathrm{got}\:\:\mathrm{19}\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 25/Apr/20
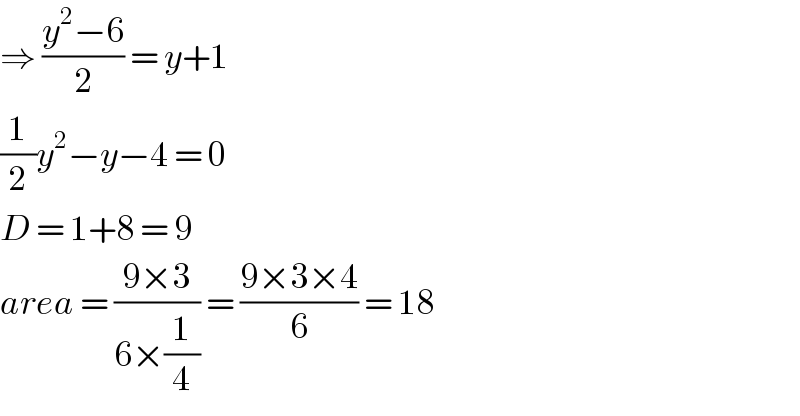
$$\Rightarrow\:\frac{{y}^{\mathrm{2}} −\mathrm{6}}{\mathrm{2}}\:=\:{y}+\mathrm{1}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} −{y}−\mathrm{4}\:=\:\mathrm{0} \\ $$$${D}\:=\:\mathrm{1}+\mathrm{8}\:=\:\mathrm{9} \\ $$$${area}\:=\:\frac{\mathrm{9}×\mathrm{3}}{\mathrm{6}×\frac{\mathrm{1}}{\mathrm{4}}}\:=\:\frac{\mathrm{9}×\mathrm{3}×\mathrm{4}}{\mathrm{6}}\:=\:\mathrm{18} \\ $$
Commented by john santu last updated on 25/Apr/20
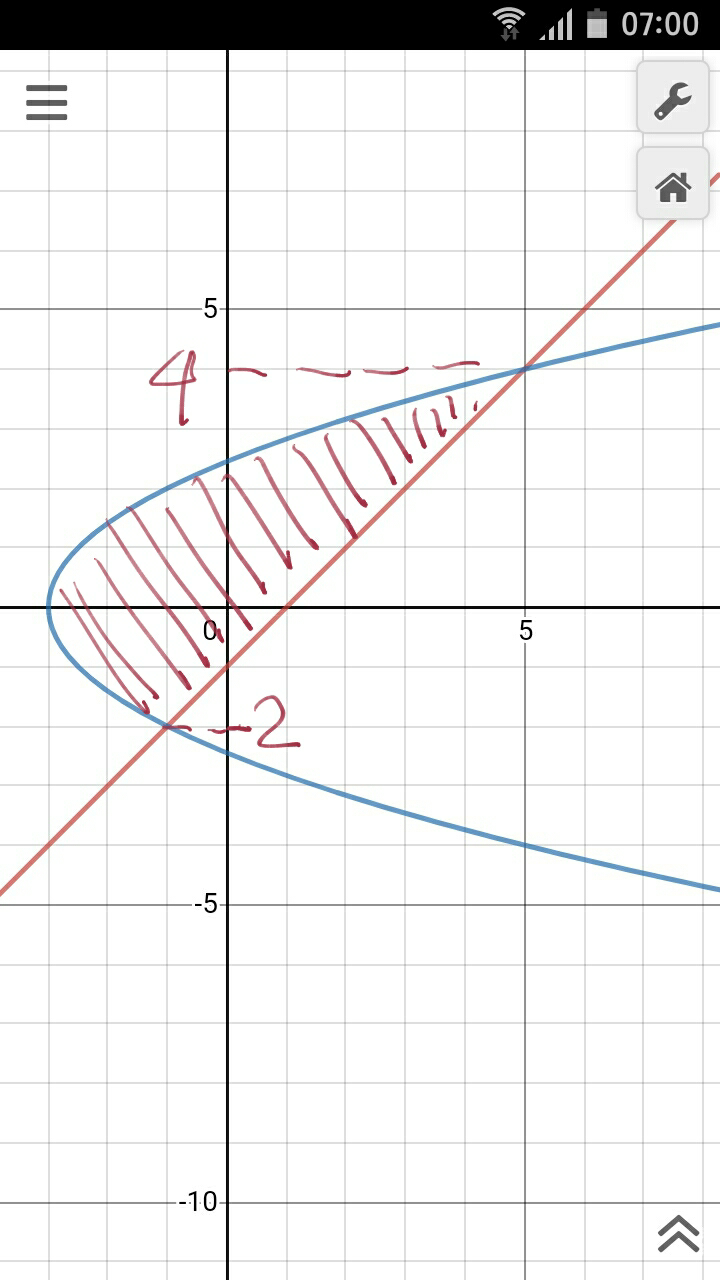
Commented by john santu last updated on 25/Apr/20
![area = ∫ _(−2) ^4 (y+1)−(((y^2 −6)/2)) dy = [(1/2)(y+1)^2 −(1/2)((1/3)y^3 −6y) ]_(−2) ^( 4) = ((1/2)(y+1)^2 −(1/6)y^3 +3y) _(−2) ^4 = (1/2)(25−1)−(1/6)(64+8)+3(6) = 12−12+18 = 18](https://www.tinkutara.com/question/Q90619.png)
$${area}\:=\:\int\underset{−\mathrm{2}} {\overset{\mathrm{4}} {\:}}\:\left({y}+\mathrm{1}\right)−\left(\frac{{y}^{\mathrm{2}} −\mathrm{6}}{\mathrm{2}}\right)\:{dy} \\ $$$$=\:\left[\frac{\mathrm{1}}{\mathrm{2}}\left({y}+\mathrm{1}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}{y}^{\mathrm{3}} −\mathrm{6}{y}\right)\:\underset{−\mathrm{2}} {\overset{\:\:\mathrm{4}} {\right]}} \\ $$$$=\:\left(\frac{\mathrm{1}}{\mathrm{2}}\left({y}+\mathrm{1}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{6}}{y}^{\mathrm{3}} +\mathrm{3}{y}\right)\underset{−\mathrm{2}} {\overset{\mathrm{4}} {\:}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{25}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{64}+\mathrm{8}\right)+\mathrm{3}\left(\mathrm{6}\right) \\ $$$$=\:\mathrm{12}−\mathrm{12}+\mathrm{18}\:=\:\mathrm{18}\: \\ $$
Commented by john santu last updated on 25/Apr/20

$${you}\:{answer}\:{false}! \\ $$
Commented by mr W last updated on 25/Apr/20
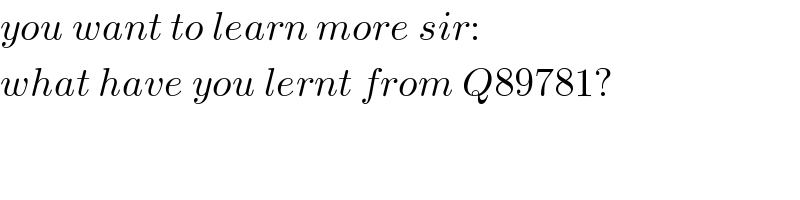
$${you}\:{want}\:{to}\:{learn}\:{more}\:{sir}: \\ $$$${what}\:{have}\:{you}\:{lernt}\:{from}\:{Q}\mathrm{89781}? \\ $$
Commented by I want to learn more last updated on 26/Apr/20
$$\mathrm{Slight}\:\mathrm{mistake}\:\mathrm{sir},\:\mathrm{thanks},\:\mathrm{next}\:\mathrm{time}, \\ $$$$\mathrm{i}\:\mathrm{will}\:\mathrm{be}\:\mathrm{careful}.\:\:\mathrm{I}\:\mathrm{appreciate} \\ $$
