Question Number 24293 by Tinkutara last updated on 15/Nov/17

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{of}\:\mathrm{a}\:\mathrm{uniform} \\ $$$$\left({a}\right)\:\mathrm{half}-\mathrm{disc},\:\left({b}\right)\:\mathrm{quarter}-\mathrm{disc}. \\ $$
Commented by ajfour last updated on 15/Nov/17
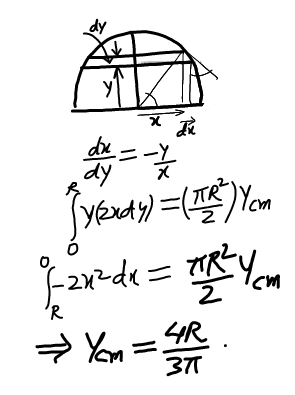
Commented by ajfour last updated on 15/Nov/17

Answered by mrW1 last updated on 15/Nov/17
![radius = R (a) semi disc θ∈[0,π] ∫_0 ^( π) (1/2)R×R×((2Rsin θ)/3)dθ=(R^3 /3)∫_0 ^( π) sin θdθ=((2R^3 )/3) y_C =((2R^3 ×2)/(3×πR^2 ))=((4R)/(3π)) (b) quarter disc θ∈[(π/4),((3π)/4)] ∫_(π/4) ^( ((3π)/4)) (1/2)R×R×((2Rsin θ)/3)dθ=(R^3 /3)∫_(π/4) ^( ((3π)/4)) sin θdθ=(((√2)R^3 )/3) y_C =(((√2)R^3 ×4)/(3×πR^2 ))=((4(√2)R)/(3π)) (c) any sector of disc with angle α (R^3 /3)∫_((π−α)/2) ^( ((π+α)/2)) sin θ dθ=((2R^3 )/3)sin (α/2) y_C =((2R^3 sin (α/2))/(3×πR^2 ×(α/(2π))))=((4R)/(3α))×sin (α/2)](https://www.tinkutara.com/question/Q24325.png)
$${radius}\:=\:{R} \\ $$$$\left({a}\right)\:{semi}\:{disc} \\ $$$$\theta\in\left[\mathrm{0},\pi\right] \\ $$$$\int_{\mathrm{0}} ^{\:\pi} \frac{\mathrm{1}}{\mathrm{2}}{R}×{R}×\frac{\mathrm{2}{R}\mathrm{sin}\:\theta}{\mathrm{3}}{d}\theta=\frac{{R}^{\mathrm{3}} }{\mathrm{3}}\int_{\mathrm{0}} ^{\:\pi} \mathrm{sin}\:\theta{d}\theta=\frac{\mathrm{2}{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${y}_{{C}} =\frac{\mathrm{2}{R}^{\mathrm{3}} ×\mathrm{2}}{\mathrm{3}×\pi{R}^{\mathrm{2}} }=\frac{\mathrm{4}{R}}{\mathrm{3}\pi} \\ $$$$ \\ $$$$\left({b}\right)\:{quarter}\:{disc} \\ $$$$\theta\in\left[\frac{\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}}\right] \\ $$$$\int_{\frac{\pi}{\mathrm{4}}} ^{\:\frac{\mathrm{3}\pi}{\mathrm{4}}} \frac{\mathrm{1}}{\mathrm{2}}{R}×{R}×\frac{\mathrm{2}{R}\mathrm{sin}\:\theta}{\mathrm{3}}{d}\theta=\frac{{R}^{\mathrm{3}} }{\mathrm{3}}\int_{\frac{\pi}{\mathrm{4}}} ^{\:\frac{\mathrm{3}\pi}{\mathrm{4}}} \mathrm{sin}\:\theta{d}\theta=\frac{\sqrt{\mathrm{2}}{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${y}_{{C}} =\frac{\sqrt{\mathrm{2}}{R}^{\mathrm{3}} ×\mathrm{4}}{\mathrm{3}×\pi{R}^{\mathrm{2}} }=\frac{\mathrm{4}\sqrt{\mathrm{2}}{R}}{\mathrm{3}\pi} \\ $$$$ \\ $$$$\left({c}\right)\:{any}\:{sector}\:{of}\:{disc}\:{with}\:{angle}\:\alpha \\ $$$$\frac{{R}^{\mathrm{3}} }{\mathrm{3}}\int_{\frac{\pi−\alpha}{\mathrm{2}}} ^{\:\frac{\pi+\alpha}{\mathrm{2}}} \mathrm{sin}\:\theta\:{d}\theta=\frac{\mathrm{2}{R}^{\mathrm{3}} }{\mathrm{3}}\mathrm{sin}\:\frac{\alpha}{\mathrm{2}} \\ $$$${y}_{{C}} =\frac{\mathrm{2}{R}^{\mathrm{3}} \mathrm{sin}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{3}×\pi{R}^{\mathrm{2}} ×\frac{\alpha}{\mathrm{2}\pi}}=\frac{\mathrm{4}{R}}{\mathrm{3}\alpha}×\mathrm{sin}\:\frac{\alpha}{\mathrm{2}} \\ $$
Commented by mrW1 last updated on 15/Nov/17

Commented by mrW1 last updated on 16/Nov/17

$${I}\:{gave}\:{a}\:{general}\:{method}\:{to}\:{determine} \\ $$$${the}\:{center}\:{of}\:{mass}.\:{It}\:{is}\:{always}\:{on} \\ $$$${the}\:{symmetric}\:{line}.\:{You}\:{only}\:{need}\:{to} \\ $$$${know}\:{the}\:{distance}\:{from}\:{the}\:{COM}\:{to} \\ $$$${the}\:{center}\:{of}\:{circle}.\:{You}\:{can}\:{see}\:{I}\:{have} \\ $$$${placed}\:{the}\:{disc}\:{such}\:{that}\:{its}\:{symmetric} \\ $$$${line}\:{is}\:{the}\:{y}−{axis}.\:{Then}\:{we}\:{only}\:{need} \\ $$$${y}_{{C}} ,\:{since}\:{x}_{{C}} =\mathrm{0}.\:{In}\:{case}\:{of}\:{quarter}−{disc}, \\ $$$${y}_{{C}} =\frac{\mathrm{4}\sqrt{\mathrm{2}}{R}}{\mathrm{3}\pi}.\:{If}\:{you}\:{at}\:{all}\:{costs}\:{want}\:{to} \\ $$$${use}\:{your}\:{coordinate}\:{system}\:{then}\:{you} \\ $$$${will}\:{get}\:{x}_{{C}} '=\frac{\mathrm{4}\sqrt{\mathrm{2}}{R}}{\mathrm{3}\pi}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\mathrm{4}{R}}{\mathrm{3}\pi},\: \\ $$$${y}_{{c}} '=\frac{\mathrm{4}\sqrt{\mathrm{2}}{R}}{\mathrm{3}\pi}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\mathrm{4}{R}}{\mathrm{3}\pi}. \\ $$$$ \\ $$$${Using}\:{my}\:{method}\:{you}\:{can}\:{easily} \\ $$$${determine}\:{the}\:{COM}\:{of}\:{any}\:{angled} \\ $$$${disc}\:{sector},\:{and}\:{you}\:{only}\:{need}\:{to} \\ $$$${know}\:{one}\:{value}\:{instead}\:{of}\:{two}. \\ $$
Commented by mrW1 last updated on 16/Nov/17

Commented by Tinkutara last updated on 16/Nov/17
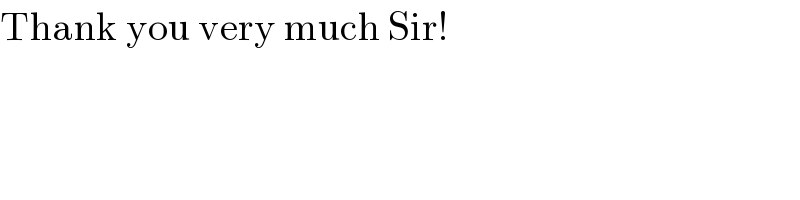
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
