Question Number 85262 by Rio Michael last updated on 20/Mar/20

$$\mathrm{find}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{symmetry}\:\mathrm{of}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\:\:\:{y}\:=\:\frac{\mathrm{1}}{{x}\:+\:\mathrm{2}} \\ $$
Commented by john santu last updated on 20/Mar/20

$$\mathrm{y}\:=−\:\mathrm{x}−\mathrm{2} \\ $$$$\mathrm{typo}\: \\ $$
Commented by Rio Michael last updated on 20/Mar/20

$${how}\:{come}\:{sir} \\ $$
Commented by mr W last updated on 20/Mar/20

$${symmetry}\:{center}\:{is}\:\left(−\mathrm{2},\mathrm{0}\right) \\ $$$${symmetry}\:{axes}\:{are} \\ $$$${y}={x}+\mathrm{2}\:{and} \\ $$$${y}=−{x}−\mathrm{2} \\ $$
Commented by Rio Michael last updated on 20/Mar/20

$$\mathrm{is}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{symmetry}\:\mathrm{thesame}\:\mathrm{as} \\ $$$$\mathrm{the}\:\mathrm{vertical}\:\mathrm{asymptote} \\ $$
Commented by mr W last updated on 20/Mar/20

$${no}\:{all}\:{symmetrical}\:{curves}\:{have}\:{a} \\ $$$${asymptote},\:{e}.{g}.\:{an}\:{ellipse}\:{or}\:{a}\:{parabola}. \\ $$$${an}\:{ellipse}\:{has}\:{two}\:{symmetry}\:{axes}, \\ $$$${therefore}\:{also}\:{a}\:{symmetry}\:{center}. \\ $$$${a}\:{parabola}\:{has}\:{only}\:{one}\:{symmetry} \\ $$$${axis},\:{therefore}\:{it}\:{has}\:{no}\:{symmetry} \\ $$$${center}. \\ $$
Commented by Rio Michael last updated on 20/Mar/20

$$\mathrm{thanks}\:\mathrm{alot}\:\mathrm{sir} \\ $$
Answered by john santu last updated on 20/Mar/20
Commented by john santu last updated on 20/Mar/20

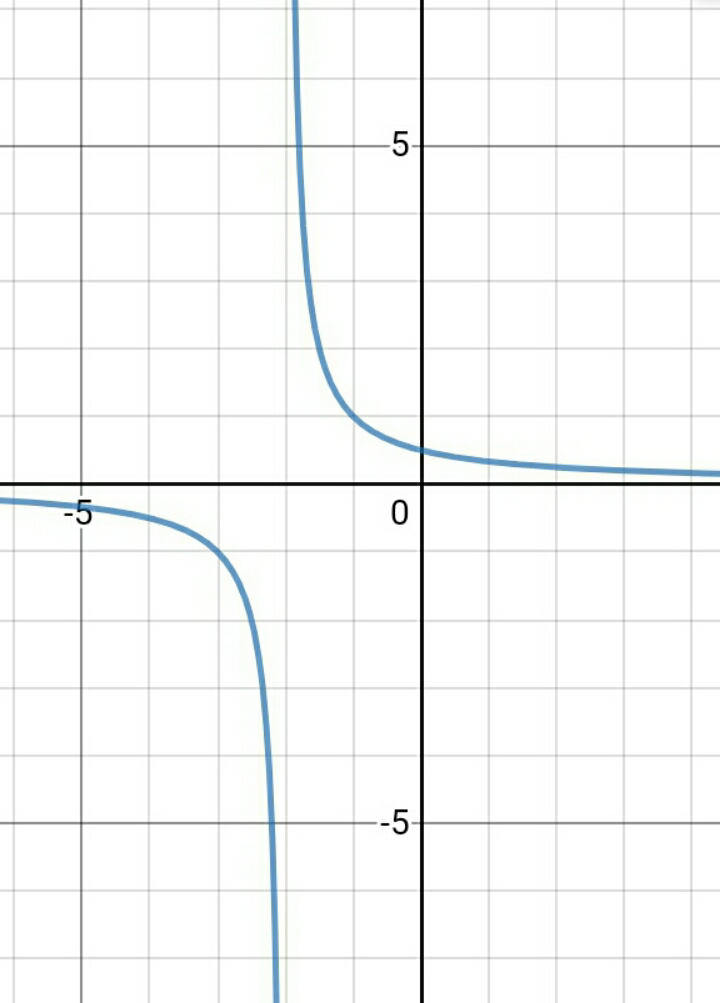
$$\mathrm{center}\:\mathrm{point}\:\left(−\mathrm{2},\mathrm{0}\right) \\ $$$$ \\ $$
Commented by mr W last updated on 20/Mar/20

Commented by Rio Michael last updated on 20/Mar/20

$$\mathrm{thanks} \\ $$
Commented by mr W last updated on 20/Mar/20

$${if}\:{a}\:{curve}\:{has}\:{two}\:{or}\:{more}\:{symmetry} \\ $$$${axes},\:{then}\:{the}\:{intersection}\:{point}\:{of} \\ $$$${the}\:{symmetry}\:{axes}\:{is}\:{the}\:{symmetry} \\ $$$${center}. \\ $$
Commented by jagoll last updated on 20/Mar/20

$$\mathrm{what}\:\mathrm{generally}\:\mathrm{formula}\:\mathrm{to}\:\mathrm{find} \\ $$$$\mathrm{the}\:\mathrm{symetri}? \\ $$
Commented by jagoll last updated on 20/Mar/20

$$\mathrm{if}\:\mathrm{y}\:=\:\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:,\:\mathrm{what}\:\mathrm{the}\:\mathrm{symetri}\:\mathrm{sir} \\ $$
Commented by jagoll last updated on 20/Mar/20

$$\mathrm{the}\:\mathrm{graph}\:\mathrm{have}\:\mathrm{1}\:\mathrm{axes}\:\mathrm{symetri} \\ $$$$ \\ $$
Commented by mr W last updated on 20/Mar/20

$${there}\:{are}\:{some}\:{easy}\:{cases}\:{to}\:“{see}''\:{the} \\ $$$${symmetry}: \\ $$$${curve}\:{y}={f}\left({x}\right) \\ $$$${if}\:{f}\left({a}+{x}\right)={f}\left({a}−{x}\right),\:{then}\:{x}={a}\:{is}\:{a} \\ $$$${symmetry}\:{axis}. \\ $$$${e}.{g}.\:{y}={f}\left({x}\right)=\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}, \\ $$$${f}\left({x}\right)={f}\left(−{x}\right)\:\Rightarrow{x}=\mathrm{0}\:{is}\:{a}\:{symmetry}\:{axis}. \\ $$$$ \\ $$$${curve}\:{x}={f}\left({y}\right) \\ $$$${if}\:{f}\left({b}+{y}\right)={f}\left({b}−{y}\right),\:{then}\:{y}={b}\:{is}\:{a} \\ $$$${symmetry}\:{axis}. \\ $$
Commented by jagoll last updated on 20/Mar/20

$$\mathrm{ok}\:\mathrm{sir}.\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mr W last updated on 20/Mar/20

$${general}\:{case}: \\ $$$${say}\:{we}\:{have}\:{a}\:{curve}\:{F}\left({x},{y}\right)=\mathrm{0}, \\ $$$${if}\:{F}\left({x}−\frac{\mathrm{2}{a}\left({ax}+{by}+{c}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} },\:{y}−\frac{\mathrm{2}{b}\left({ax}+{by}+{c}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)={F}\left({x},\:{y}\right), \\ $$$${then}\:{ax}+{by}+{c}=\mathrm{0}\:{is}\:{a}\:{symmetry}\:{axis}. \\ $$$${why}? \\ $$$${see}\:{Q}\mathrm{84531} \\ $$$${if}\:{F}\left({x}−\frac{\mathrm{2}{a}\left({ax}+{by}+{c}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} },\:{y}−\frac{\mathrm{2}{b}\left({ax}+{by}+{c}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)={F}\left({x},\:{y}\right), \\ $$$${that}\:{means}\:{the}\:{image}\:{of}\:{curve}\:{F}\left({x},{y}\right) \\ $$$${in}\:{the}\:{line}\:{ax}+{by}+{c}=\mathrm{0}\:{is}\:{the}\:{curve} \\ $$$${itself},\:{this}\:{is}\:{the}\:{case}\:{when}\:{the}\:{curve} \\ $$$${is}\:{symmetric}\:{about}\:{the}\:{line} \\ $$$${ax}+{by}+{c}=\mathrm{0}. \\ $$
