Find-the-centre-of-the-mass-of-a-cone-of-height-H-and-Radius-R-

Question Number 105073 by Dwaipayan Shikari last updated on 25/Jul/20

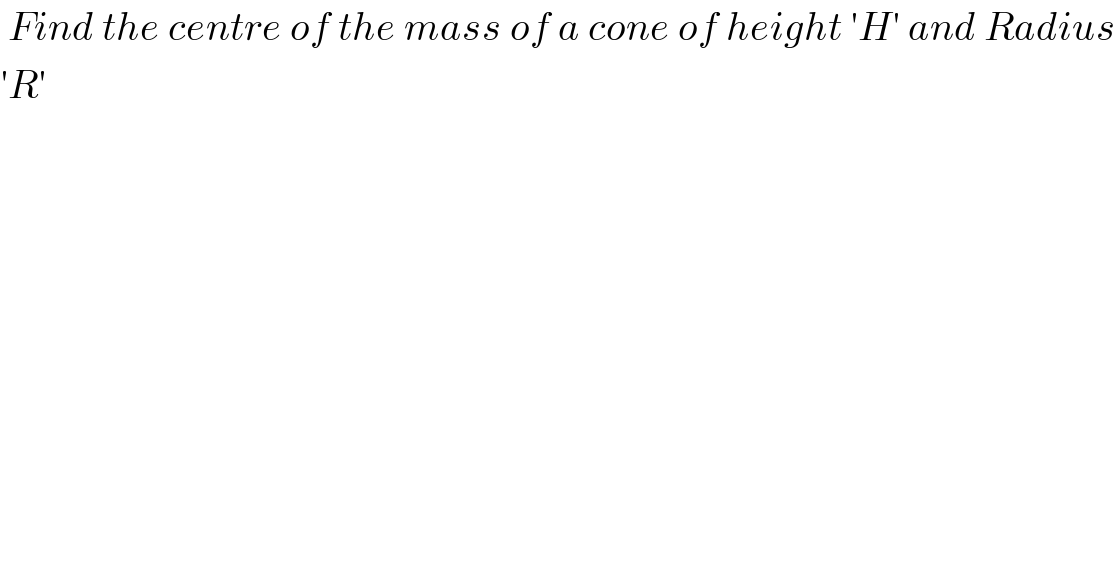
$$\:{Find}\:{the}\:{centre}\:{of}\:{the}\:{mass}\:{of}\:{a}\:{cone}\:{of}\:{height}\:'{H}'\:{and}\:{Radius} \\ $$$$'{R}' \\ $$

Commented by ajfour last updated on 25/Jul/20

$${solid}\:{cone}\:{or}\:{hollow}\:? \\ $$

Commented by Dwaipayan Shikari last updated on 25/Jul/20

$${Solid}\:{sir} \\ $$

Commented by mr W last updated on 25/Jul/20

Commented by mr W last updated on 25/Jul/20

for a solid cone the distribution of mass is a parabola of second order, therefore y_S =(H/4).

$${for}\:{a}\:{solid}\:{cone}\:{the}\:{distribution}\:{of} \\ $$$${mass}\:{is}\:{a}\:{parabola}\:{of}\:{second}\:{order}, \\ $$$${therefore}\:{y}_{{S}} =\frac{{H}}{\mathrm{4}}. \\ $$

Answered by ajfour last updated on 25/Jul/20

Commented by ajfour last updated on 25/Jul/20

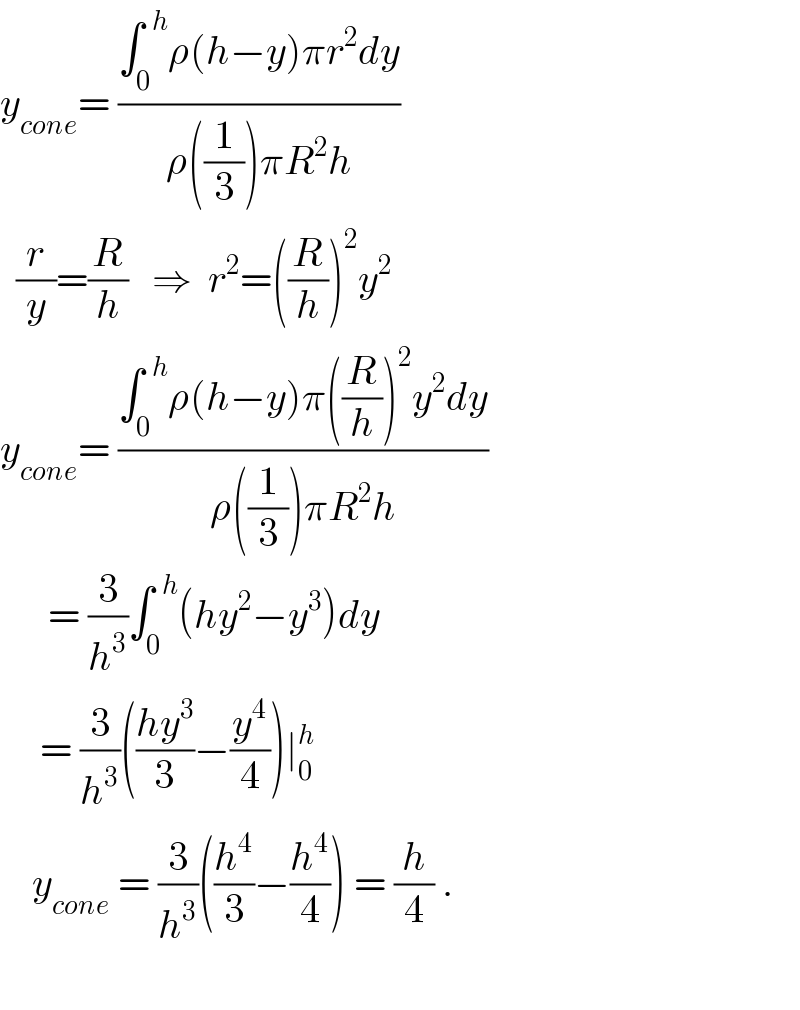
y_(cone) = ((∫_0 ^( h) ρ(h−y)πr^2 dy)/(ρ((1/3))πR^2 h)) (r/y)=(R/h) ⇒ r^2 =((R/h))^2 y^2 y_(cone) = ((∫_0 ^( h) ρ(h−y)π((R/h))^2 y^2 dy)/(ρ((1/3))πR^2 h)) = (3/h^3 )∫_0 ^( h) (hy^2 −y^3 )dy = (3/h^3 )(((hy^3 )/3)−(y^4 /4))∣_0 ^h y_(cone) = (3/h^3 )((h^4 /3)−(h^4 /4)) = (h/4) .

$${y}_{{cone}} =\:\frac{\int_{\mathrm{0}} ^{\:\:{h}} \rho\left({h}−{y}\right)\pi{r}^{\mathrm{2}} {dy}}{\rho\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\pi{R}^{\mathrm{2}} {h}} \\ $$$$\:\:\frac{{r}}{{y}}=\frac{{R}}{{h}}\:\:\:\Rightarrow\:\:{r}^{\mathrm{2}} =\left(\frac{{R}}{{h}}\right)^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$${y}_{{cone}} =\:\frac{\int_{\mathrm{0}} ^{\:\:{h}} \rho\left({h}−{y}\right)\pi\left(\frac{{R}}{{h}}\right)^{\mathrm{2}} {y}^{\mathrm{2}} {dy}}{\rho\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\pi{R}^{\mathrm{2}} {h}} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{3}}{{h}^{\mathrm{3}} }\int_{\mathrm{0}} ^{\:\:{h}} \left({hy}^{\mathrm{2}} −{y}^{\mathrm{3}} \right){dy}\: \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{3}}{{h}^{\mathrm{3}} }\left(\frac{{hy}^{\mathrm{3}} }{\mathrm{3}}−\frac{{y}^{\mathrm{4}} }{\mathrm{4}}\right)\mid_{\mathrm{0}} ^{{h}} \\ $$$$\:\:\:\:{y}_{{cone}} \:=\:\frac{\mathrm{3}}{{h}^{\mathrm{3}} }\left(\frac{{h}^{\mathrm{4}} }{\mathrm{3}}−\frac{{h}^{\mathrm{4}} }{\mathrm{4}}\right)\:=\:\frac{{h}}{\mathrm{4}}\:. \\ $$$$ \\ $$

Commented by Dwaipayan Shikari last updated on 25/Jul/20

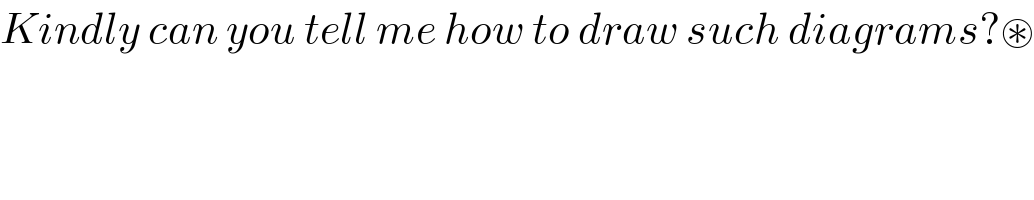
$${Kindly}\:{can}\:{you}\:{tell}\:{me}\:{how}\:{to}\:{draw}\:{such}\:{diagrams}?\circledast \\ $$

Commented by ajfour last updated on 25/Jul/20

$${i}\:{use}\:{lekh}\:{diagram}\:{app}. \\ $$

Commented by Dwaipayan Shikari last updated on 25/Jul/20

��

Facebook Tweet Pin

Find-the-centre-of-the-mass-of-a-cone-of-height-H-and-Radius-R-

Leave a Reply Cancel reply