Question Number 58373 by Tawa1 last updated on 22/Apr/19
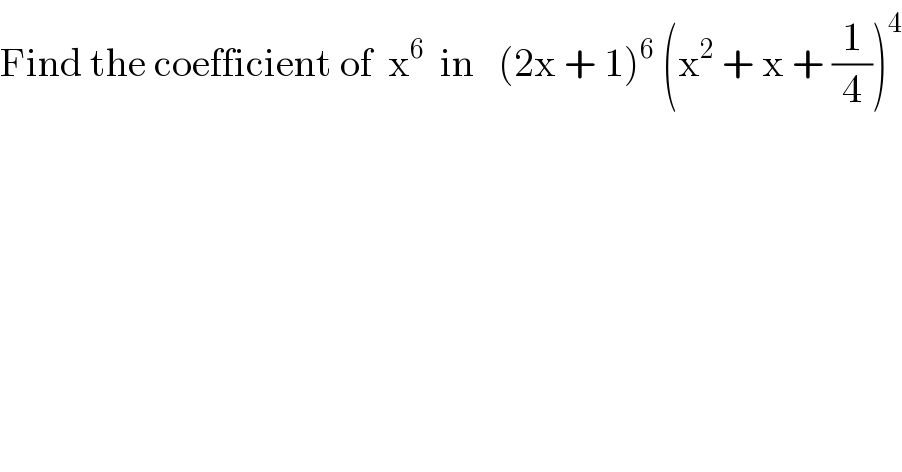
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\:\mathrm{x}^{\mathrm{6}} \:\:\mathrm{in}\:\:\:\left(\mathrm{2x}\:+\:\mathrm{1}\right)^{\mathrm{6}} \:\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{x}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{4}} \\ $$
Commented by maxmathsup by imad last updated on 24/Apr/19
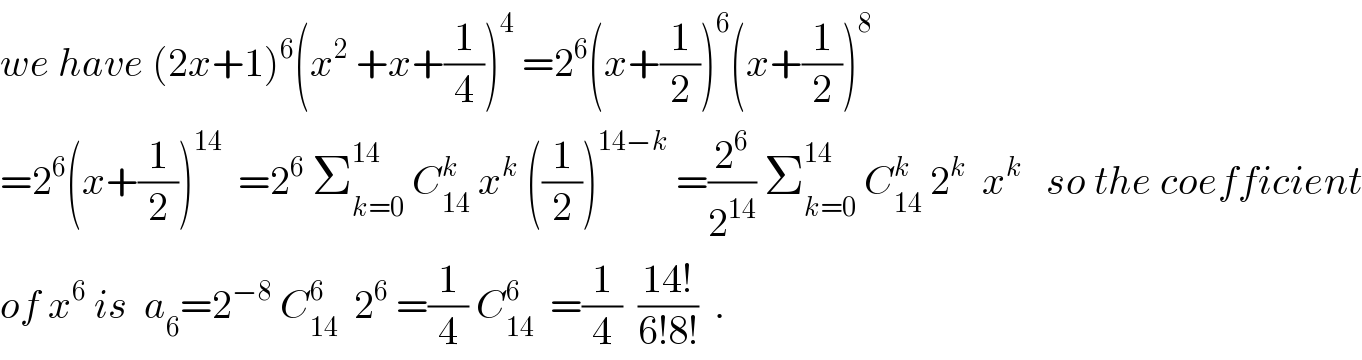
$${we}\:{have}\:\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{6}} \left({x}^{\mathrm{2}} \:+{x}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{4}} \:=\mathrm{2}^{\mathrm{6}} \left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{6}} \left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{8}} \\ $$$$=\mathrm{2}^{\mathrm{6}} \left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{14}} \:\:=\mathrm{2}^{\mathrm{6}} \:\sum_{{k}=\mathrm{0}} ^{\mathrm{14}} \:{C}_{\mathrm{14}} ^{{k}} \:{x}^{{k}} \:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{14}−{k}} \:=\frac{\mathrm{2}^{\mathrm{6}} }{\mathrm{2}^{\mathrm{14}} }\:\sum_{{k}=\mathrm{0}} ^{\mathrm{14}} \:{C}_{\mathrm{14}} ^{{k}} \:\mathrm{2}^{{k}} \:\:{x}^{{k}} \:\:\:{so}\:{the}\:{coefficient} \\ $$$${of}\:{x}^{\mathrm{6}} \:{is}\:\:{a}_{\mathrm{6}} =\mathrm{2}^{−\mathrm{8}} \:{C}_{\mathrm{14}} ^{\mathrm{6}} \:\:\mathrm{2}^{\mathrm{6}} \:=\frac{\mathrm{1}}{\mathrm{4}}\:{C}_{\mathrm{14}} ^{\mathrm{6}} \:\:=\frac{\mathrm{1}}{\mathrm{4}}\:\:\frac{\mathrm{14}!}{\mathrm{6}!\mathrm{8}!}\:\:. \\ $$
Answered by tanmay last updated on 22/Apr/19
![(2x+1)^6 [(x+(1/2))^2 ]^4 (2x+1)^6 (x+(1/2))^8 or method (2x+1)^6 [(x+(1/2))^2 ]^4 =2^6 (x+(1/2))^6 (x+(1/2))^8 =2^6 (x+(1/2))^(14) =2^6 ×14c_8 ×x^6 ×((1/2))^8 =((14×13×12×11×10×9)/(6×5×4×3×2×2^2 )) =((14×13×11×9)/(6×4)) =((7×13×11×3)/4)=((3003)/4)](https://www.tinkutara.com/question/Q58399.png)
$$\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{6}} \left[\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right]^{\mathrm{4}} \\ $$$$\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{6}} \left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{8}} \\ $$$$\: \\ $$$$\boldsymbol{{or}}\:\boldsymbol{{method}} \\ $$$$\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{1}\right)^{\mathrm{6}} \left[\left(\boldsymbol{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right]^{\mathrm{4}} \\ $$$$=\mathrm{2}^{\mathrm{6}} \left(\boldsymbol{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{6}} \left(\boldsymbol{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{8}} \\ $$$$=\mathrm{2}^{\mathrm{6}} \left(\boldsymbol{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{14}} \\ $$$$=\mathrm{2}^{\mathrm{6}} ×\mathrm{14}\boldsymbol{{c}}_{\mathrm{8}} ×\boldsymbol{{x}}^{\mathrm{6}} ×\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{8}} \\ $$$$=\frac{\mathrm{14}×\mathrm{13}×\mathrm{12}×\mathrm{11}×\mathrm{10}×\mathrm{9}}{\mathrm{6}×\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{2}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{14}×\mathrm{13}×\mathrm{11}×\mathrm{9}}{\mathrm{6}×\mathrm{4}} \\ $$$$=\frac{\mathrm{7}×\mathrm{13}×\mathrm{11}×\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{3003}}{\mathrm{4}} \\ $$
Commented by Tawa1 last updated on 23/Apr/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
