Menu Close

find-the-coefficients-of-x-2-and-x-3-terms-in-the-expansion-of-1-x-1-2x-2-1-3x-3-1-100x-100-

Tinku Tara 0 Comments
Pin




Question Number 85902 by mr W last updated on 26/Mar/20
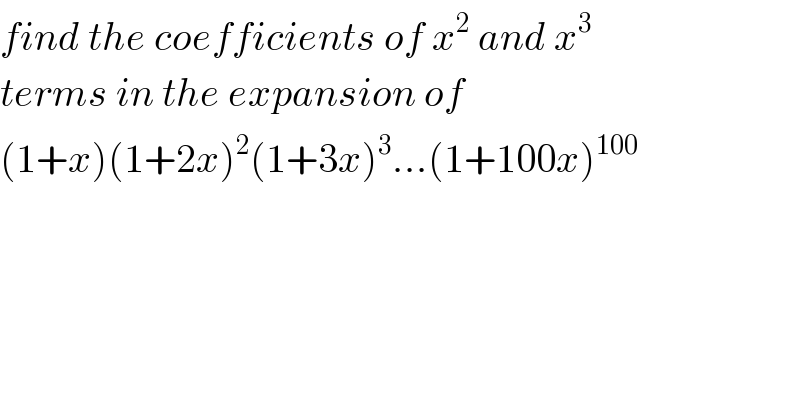
find the coefficients of x^2 and x^3 terms in the expansion of (1+x)(1+2x)^2 (1+3x)^3 ...(1+100x)^(100)
$${find}\:{the}\:{coefficients}\:{of}\:{x}^{\mathrm{2}} \:{and}\:{x}^{\mathrm{3}} \: \\ $$$${terms}\:{in}\:{the}\:{expansion}\:{of} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\mathrm{2}{x}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3}{x}\right)^{\mathrm{3}} …\left(\mathrm{1}+\mathrm{100}{x}\right)^{\mathrm{100}} \\ $$
Commented by Serlea last updated on 26/Mar/20
Ok From my analysis, it′s 21868 and 1400 How? Starting (1+x)= Doesn^′ t exist (1+x)(1+2x)^2 =4 and 8 (1+x)(1+2x)^2 (1+3x)^3 =238 and 80 { 238x^3 +80x^2 +14x+1} (1+x)(1+2x)^2 (1+3x)^3 (1+4x)^4 =3118 and 400 {3118x^3 +400x^2 +30x+1} It′s impossible to calculate to the end Buy let try the next two (1+x)(1+2x)^2 (1+3x)^3 (1+4x)^4 (1+5x)^5 =21868 and 1400 {21868x^3 +1400x^2 +55x+1} (1+x)(1+2x)^2 (1+3x)^3 (1+4x)^4 (1+5x)^5 (1+6x)^6 ⇒ 21868(1+6x)^6 x^3 +1400(1+6x)^6 x^2 +55(1+6x)^6 +(1+6x)^6 ⇊_(21868x^3 ) ⇊_(1400x^2 ) With this, The coeff. remains constant for 21868 and 1400
$$\mathrm{Ok} \\ $$$$\mathrm{From}\:\mathrm{my}\:\:\mathrm{analysis},\:\mathrm{it}'\mathrm{s}\:\mathrm{21868}\:\mathrm{and}\:\mathrm{1400} \\ $$$$\boldsymbol{\mathrm{How}}? \\ $$$$\mathrm{Starting}\:\left(\mathrm{1}+\mathrm{x}\right)=\:\mathrm{Doesn}^{'} \mathrm{t}\:\mathrm{exist} \\ $$$$\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\mathrm{2x}\right)^{\mathrm{2}} =\mathrm{4}\:\mathrm{and}\:\mathrm{8} \\ $$$$\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\mathrm{2x}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3x}\right)^{\mathrm{3}} =\mathrm{238}\:\mathrm{and}\:\mathrm{80} \\ $$$$\left\{\:\mathrm{238x}^{\mathrm{3}} +\mathrm{80x}^{\mathrm{2}} +\mathrm{14x}+\mathrm{1}\right\} \\ $$$$\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\mathrm{2x}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3x}\right)^{\mathrm{3}} \left(\mathrm{1}+\mathrm{4x}\right)^{\mathrm{4}} =\mathrm{3118}\:\mathrm{and}\:\mathrm{400} \\ $$$$\left\{\mathrm{3118x}^{\mathrm{3}} +\mathrm{400x}^{\mathrm{2}} +\mathrm{30x}+\mathrm{1}\right\} \\ $$$$\:\mathrm{It}'\mathrm{s}\:\mathrm{impossible}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{to}\:\mathrm{the}\:\mathrm{end}\:\boldsymbol{\mathrm{B}}\mathrm{uy} \\ $$$$\mathrm{let}\:\mathrm{try}\:\mathrm{the}\:\mathrm{next}\:\mathrm{two} \\ $$$$\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\mathrm{2x}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3x}\right)^{\mathrm{3}} \left(\mathrm{1}+\mathrm{4x}\right)^{\mathrm{4}} \left(\mathrm{1}+\mathrm{5x}\right)^{\mathrm{5}} =\mathrm{21868}\:\mathrm{and}\:\mathrm{1400} \\ $$$$\left\{\mathrm{21868x}^{\mathrm{3}} +\mathrm{1400x}^{\mathrm{2}} +\mathrm{55x}+\mathrm{1}\right\} \\ $$$$\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\mathrm{2x}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3x}\right)^{\mathrm{3}} \left(\mathrm{1}+\mathrm{4x}\right)^{\mathrm{4}} \left(\mathrm{1}+\mathrm{5x}\right)^{\mathrm{5}} \left(\mathrm{1}+\mathrm{6x}\right)^{\mathrm{6}} \\ $$$$\Rightarrow\:\mathrm{21868}\left(\mathrm{1}+\mathrm{6}\boldsymbol{\mathrm{x}}\right)^{\mathrm{6}} \boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{1400}\left(\mathrm{1}+\mathrm{6}\boldsymbol{\mathrm{x}}\right)^{\mathrm{6}} \mathrm{x}^{\mathrm{2}} +\mathrm{55}\left(\mathrm{1}+\mathrm{6}\boldsymbol{\mathrm{x}}\right)^{\mathrm{6}} +\left(\mathrm{1}+\mathrm{6}\boldsymbol{\mathrm{x}}\right)^{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{\mathrm{21868x}^{\mathrm{3}} } {\downdownarrows}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{\mathrm{1400x}^{\mathrm{2}} } {\downdownarrows} \\ $$$$ \\ $$$$\mathrm{With}\:\mathrm{this},\:\mathrm{The}\:\mathrm{coeff}.\:\mathrm{remains}\:\mathrm{constant}\:\mathrm{for} \\ $$$$\mathrm{21868}\:\mathrm{and}\:\mathrm{1400} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 26/Mar/20
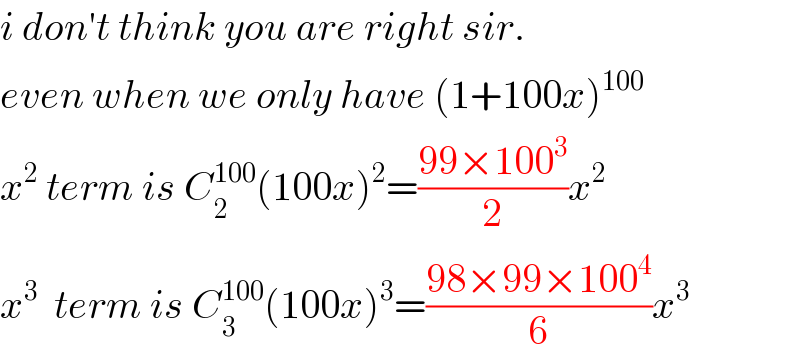
i don′t think you are right sir. even when we only have (1+100x)^(100) x^2 term is C_2 ^(100) (100x)^2 =((99×100^3 )/2)x^2 x^3 term is C_3 ^(100) (100x)^3 =((98×99×100^4 )/6)x^3
$${i}\:{don}'{t}\:{think}\:{you}\:{are}\:{right}\:{sir}. \\ $$$${even}\:{when}\:{we}\:{only}\:{have}\:\left(\mathrm{1}+\mathrm{100}{x}\right)^{\mathrm{100}} \\ $$$${x}^{\mathrm{2}} \:{term}\:{is}\:{C}_{\mathrm{2}} ^{\mathrm{100}} \left(\mathrm{100}{x}\right)^{\mathrm{2}} =\frac{\mathrm{99}×\mathrm{100}^{\mathrm{3}} }{\mathrm{2}}{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{3}} \:\:{term}\:{is}\:{C}_{\mathrm{3}} ^{\mathrm{100}} \left(\mathrm{100}{x}\right)^{\mathrm{3}} =\frac{\mathrm{98}×\mathrm{99}×\mathrm{100}^{\mathrm{4}} }{\mathrm{6}}{x}^{\mathrm{3}} \\ $$
Commented by Serlea last updated on 26/Mar/20
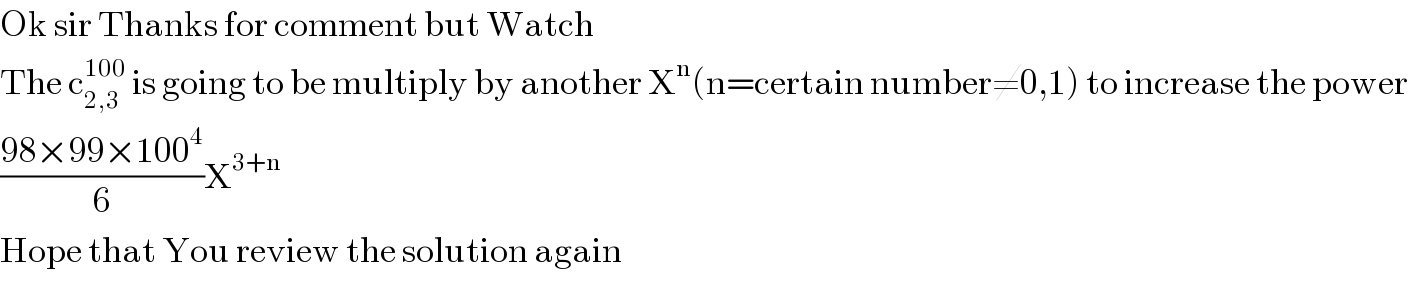
Ok sir Thanks for comment but Watch The c_(2,3) ^(100) is going to be multiply by another X^n (n=certain number≠0,1) to increase the power ((98×99×100^4 )/6)X^(3+n) Hope that You review the solution again
$$\mathrm{Ok}\:\mathrm{sir}\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{comment}\:\mathrm{but}\:\mathrm{Watch} \\ $$$$\mathrm{The}\:\mathrm{c}_{\mathrm{2},\mathrm{3}} ^{\mathrm{100}} \:\mathrm{is}\:\mathrm{going}\:\mathrm{to}\:\mathrm{be}\:\mathrm{multiply}\:\mathrm{by}\:\mathrm{another}\:\mathrm{X}^{\mathrm{n}} \left(\mathrm{n}=\mathrm{certain}\:\mathrm{number}\neq\mathrm{0},\mathrm{1}\right)\:\mathrm{to}\:\mathrm{increase}\:\mathrm{the}\:\mathrm{power} \\ $$$$\frac{\mathrm{98}×\mathrm{99}×\mathrm{100}^{\mathrm{4}} }{\mathrm{6}}\mathrm{X}^{\mathrm{3}+\mathrm{n}} \\ $$$$\mathrm{Hope}\:\mathrm{that}\:\mathrm{You}\:\mathrm{review}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{again} \\ $$
Commented by mr W last updated on 26/Mar/20
certainly i know that. i just wanted to show that your answer is wrong. i didn′t say that is the final answer what i gave. i just showed the x^2 and x^3 in (1+100x)^(100) , the coef. are already very huge. i said “even when we only...” the answer to the question is much more complicated. i′ll try later.
$${certainly}\:{i}\:{know}\:{that}. \\ $$$${i}\:{just}\:{wanted}\:{to}\:{show}\:{that}\:{your}\:{answer} \\ $$$${is}\:{wrong}.\:{i}\:{didn}'{t}\:{say}\:{that}\:{is}\:{the}\:{final} \\ $$$${answer}\:{what}\:{i}\:{gave}.\:{i}\:{just} \\ $$$${showed}\:{the}\:{x}^{\mathrm{2}} \:{and}\:{x}^{\mathrm{3}} \:{in} \\ $$$$\left(\mathrm{1}+\mathrm{100}{x}\right)^{\mathrm{100}} ,\:{the}\:{coef}.\:{are}\:{already} \\ $$$${very}\:{huge}.\:{i}\:{said}\:“{even}\:{when}\:{we}\:{only}…'' \\ $$$${the}\:{answer}\:{to}\:{the}\:{question}\:{is}\:{much} \\ $$$${more}\:{complicated}.\:{i}'{ll}\:{try}\:{later}. \\ $$
Commented by Serlea last updated on 26/Mar/20
To Look from the Open door, The coeff. Of X^2 and X^3 Will remain constant because for every Bracket, There will be a number ′′1′′ that doesn′t have a coeff. let a=coeff of x^3 for ax^3 (1+100x)^(100) ⇒1+..... So: ax^3 (1+12x+..) =ax^3 +..... That is to show that the coeff of X^3 will remain constant
$$ \\ $$$$\mathrm{To}\:\mathrm{Look}\:\mathrm{from}\:\mathrm{the}\:\mathrm{Open}\:\mathrm{door}, \\ $$$$\mathrm{The}\:\mathrm{coeff}.\:\mathrm{Of}\:\mathrm{X}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{X}^{\mathrm{3}} \:\mathrm{Will}\:\mathrm{remain} \\ $$$$\mathrm{constant}\:\mathrm{because}\:\mathrm{for}\:\mathrm{every}\:\mathrm{Bracket}, \\ $$$$\mathrm{There}\:\mathrm{will}\:\mathrm{be}\:\mathrm{a}\:\mathrm{number}\:''\mathrm{1}''\:\mathrm{that}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{have}\:\mathrm{a}\:\mathrm{coeff}. \\ $$$$\mathrm{let}\:\mathrm{a}=\mathrm{coeff}\:\mathrm{of}\:\mathrm{x}^{\mathrm{3}} \:\:\mathrm{for}\:\mathrm{ax}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{100x}\right)^{\mathrm{100}} \Rightarrow\mathrm{1}+….. \\ $$$$\:\mathrm{So}:\:\:\mathrm{ax}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{12x}+..\right) \\ $$$$=\mathrm{ax}^{\mathrm{3}} +….. \\ $$$$\mathrm{That}\:\mathrm{is}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{coeff}\:\mathrm{of}\:\mathrm{X}^{\mathrm{3}} \: \\ $$$$\mathrm{will}\:\mathrm{remain}\:\mathrm{constant}\: \\ $$$$ \\ $$
Commented by mr W last updated on 26/Mar/20
but every x term and every x^2 can also form a new x^3 term.
$${but}\:{every}\:{x}\:{term}\:{and}\:{every}\:{x}^{\mathrm{2}} \:{can}\:{also} \\ $$$${form}\:{a}\:{new}\:{x}^{\mathrm{3}} \:{term}. \\ $$
Commented by Kunal12588 last updated on 26/Mar/20
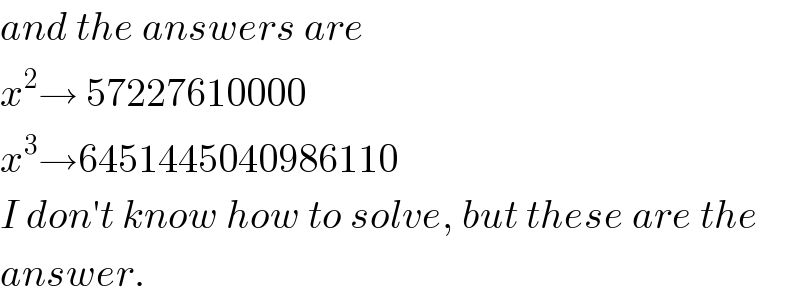
and the answers are x^2 → 57227610000 x^3 →6451445040986110 I don′t know how to solve, but these are the answer.
$${and}\:{the}\:{answers}\:{are} \\ $$$${x}^{\mathrm{2}} \rightarrow\:\mathrm{57227610000} \\ $$$${x}^{\mathrm{3}} \rightarrow\mathrm{6451445040986110} \\ $$$${I}\:{don}'{t}\:{know}\:{how}\:{to}\:{solve},\:{but}\:{these}\:{are}\:{the} \\ $$$${answer}. \\ $$
Commented by jagoll last updated on 26/Mar/20
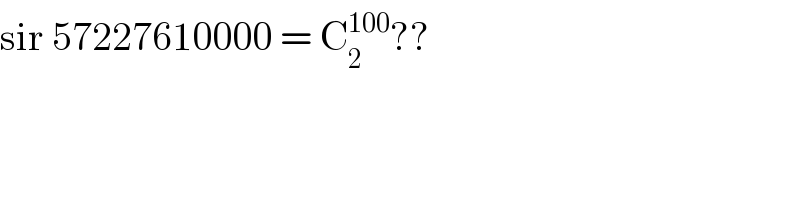
sir 57227610000 = C_2 ^(100) ??
$$\mathrm{sir}\:\mathrm{57227610000}\:=\:\mathrm{C}_{\mathrm{2}} ^{\mathrm{100}} ?? \\ $$
Commented by naka3546 last updated on 26/Mar/20
C _2 ^(100) = 4950
$${C}\underset{\mathrm{2}} {\overset{\mathrm{100}} {\:}}\:\:=\:\:\mathrm{4950}\: \\ $$
Commented by jagoll last updated on 26/Mar/20
correction C_2 ^(100) ×(100)^2
$$\mathrm{correction}\: \\ $$$$\mathrm{C}_{\mathrm{2}} ^{\mathrm{100}} ×\left(\mathrm{100}\right)^{\mathrm{2}} \\ $$
Commented by naka3546 last updated on 26/Mar/20
Commented by Serlea last updated on 26/Mar/20
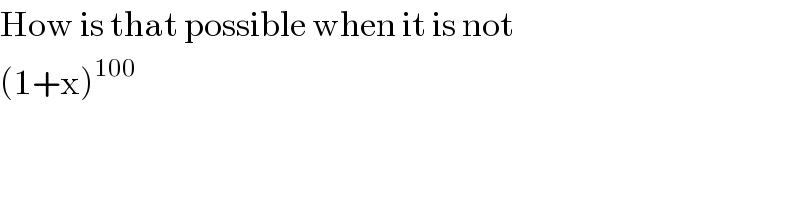
How is that possible when it is not (1+x)^(100)
$$\mathrm{How}\:\mathrm{is}\:\mathrm{that}\:\mathrm{possible}\:\mathrm{when}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not} \\ $$$$\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{100}} \\ $$
Commented by TawaTawa1 last updated on 26/Mar/20
Sir mrW. being a while sir. Please kindly help with question 85950. Please. Thanks for every time sir. I need it. God bless you sir.
$$\mathrm{Sir}\:\mathrm{mrW}.\:\mathrm{being}\:\mathrm{a}\:\mathrm{while}\:\mathrm{sir}. \\ $$$$\mathrm{Please}\:\mathrm{kindly}\:\mathrm{help}\:\mathrm{with}\:\mathrm{question}\:\:\mathrm{85950}. \\ $$$$\mathrm{Please}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{every}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{need}\:\mathrm{it}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Prithwish Sen 1 last updated on 26/Mar/20
Let (1+x)(1+2x)^2 (1+3x)^3 (1+4x)^4 and for (1+x), A^x and A^x^2 denotes the coeffi. of x and x^2 repectively similarly B , C, D for other 3 factors then for the coefficient of x^2 for the expression will be A^x .B^x +A^x .C^x +A^x .D^x +B^x .C^x +B^x .D^x +C^x .D^x + A^x^2 +B^x^2 +C^x^2 similarly for the coefficient of x^3 A^x .B^x^2 +A^x .C^x^2 +A^x .D^x^2 +B^x .C^x^2 +B^x .D^x^2 +C^x .D^x^2 +B^x^2 .C^x +B^x^2 .D^x +C^x^2 .D^x +C^x^3 +D^x^3 +A^x .B^x .C^x +A^x .B^x .D^x +A^x .C^x .D^x +B^x .C^x .D^x waiting for your response sir.
$$\mathrm{Let} \\ $$$$\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\mathrm{2x}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3x}\right)^{\mathrm{3}} \left(\mathrm{1}+\mathrm{4x}\right)^{\mathrm{4}} \\ $$$$\mathrm{and}\:\mathrm{for}\:\left(\mathrm{1}+\mathrm{x}\right),\:\mathrm{A}^{\mathrm{x}} \mathrm{and}\:\mathrm{A}^{\mathrm{x}^{\mathrm{2}} } \mathrm{denotes}\:\mathrm{the}\:\mathrm{coeffi}.\:\mathrm{of}\: \\ $$$$\mathrm{x}\:\mathrm{and}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{repectively} \\ $$$$\mathrm{similarly}\:\mathrm{B}\:,\:\mathrm{C},\:\mathrm{D}\:\mathrm{for}\:\mathrm{other}\:\mathrm{3}\:\mathrm{factors} \\ $$$$\mathrm{then}\:\mathrm{for}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:\mathrm{for}\:\mathrm{the}\:\mathrm{expression} \\ $$$$\mathrm{will}\:\mathrm{be} \\ $$$$\boldsymbol{\mathrm{A}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{A}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{A}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}} + \\ $$$$\boldsymbol{\mathrm{A}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } +\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } +\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \\ $$$$\mathrm{similarly}\:\mathrm{for}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\boldsymbol{\mathrm{x}}^{\mathrm{3}} \\ $$$$\boldsymbol{\mathrm{A}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } +\boldsymbol{\mathrm{A}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } +\boldsymbol{\mathrm{A}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } +\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } +\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } +\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \\ $$$$+\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } .\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}^{\mathrm{3}} } +\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}^{\mathrm{3}} } +\boldsymbol{\mathrm{A}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{A}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}} \\ $$$$+\boldsymbol{\mathrm{A}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{B}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{C}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{D}}^{\boldsymbol{\mathrm{x}}} \\ $$$$\boldsymbol{\mathrm{waiting}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{response}}\:\boldsymbol{\mathrm{sir}}. \\ $$
Commented by Serlea last updated on 26/Mar/20
Can u explain again I am not getting ur point
$$\mathrm{Can}\:\mathrm{u}\:\mathrm{explain}\:\mathrm{again} \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{getting}\:\mathrm{ur}\:\mathrm{point} \\ $$
Answered by mr W last updated on 06/Apr/20
let n=100 P=(1+x)(1+2x)^2 (1+3x)^3 ...(1+100x)^(100) =P_1 P_2 P_3 ...P_k ...P_n P_k =(1+kx)^k =Σ_(r=0) ^k C_r ^k (kx)^r P_k =1+k(kx)+((k(k−1))/(2!))(kx)^2 +((k(k−1)(k−2))/(3!))(kx)^3 +((k(k−1)(k−2)(k−3))/(4!))(kx)^4 +o(x^4 ) =1+k^2 x+((k^3 (k−1))/2)x^2 +((k^4 (k−1)(k−2))/6)x^3 +((k^5 (k−1)(k−2)(k−3))/(24))x^4 +o(x^4 ) ⇒P_k =1+a_(k,1) x+a_(k,2) x^2 +a_(k,3) x^3 +a_(k,4) x^4 +o(x^4 ) with a_(k^� ,1) =k^2 , a_(k,2) =((k^3 (k−1))/2), a_(k,3) =((k^4 (k−1)(k−2))/6), a_(k,4) =((k^5 (k−1)(k−2)(k−3))/(24)) k=1,2,3,...,n coef. of x term: C_1 =Σ_(k=1) ^n a_(k,1) =Σ_(k=1) ^n k^2 =((n(n+1)(2n+1))/6) with n=100, C_1 =((100×101×201)/6)=338 350 coef. of x^2 term: C_2 =Σ_(k=1) ^n Σ_(j=k+1) ^n a_(k,1) a_(j,1) +Σ_(k=1) ^n a_(k,2) =(1/2)Σ_(k=1) ^n a_(k,1) (Σ_(j=1) ^n a_(j,1) −a_(k,1) )+Σ_(k=1) ^n a_(k,2) =(1/2)[(Σ_(k=1) ^n a_(k,1) )^2 −Σ_(k=1) ^n a_(k,1) ^2 ]+Σ_(k=1) ^n a_(k^� 2) =(1/2)[(Σ_(k=1) ^n k^2 )^2 −Σ_(k=1) ^n k^4 ]+Σ_(k=1) ^n ((k^3 (k−1))/2) =(1/2)(Σ_(k=1) ^n k^2 )^2 −(1/2)Σ_(k=1) ^n k^4 +(1/2)Σ_(k=1) ^n k^4 −(1/2)Σ_(k=1) ^n k^3 =(1/2)(Σ_(k=1) ^n k^2 )^2 −(1/2)Σ_(k=1) ^n k^3 =(1/2)[((n(n+1)(2n+1))/6)]^2 −(1/2)[((n(n+1))/2)]^2 =(((n−1)n^2 (n+1)^2 (n+2))/(18)) with n=100, C_2 =((99×100^2 ×101^2 ×102)/(18))=57 227 610 000 (to be continued)
$${let}\:{n}=\mathrm{100} \\ $$$${P}=\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\mathrm{2}{x}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3}{x}\right)^{\mathrm{3}} …\left(\mathrm{1}+\mathrm{100}{x}\right)^{\mathrm{100}} \\ $$$$={P}_{\mathrm{1}} {P}_{\mathrm{2}} {P}_{\mathrm{3}} …{P}_{{k}} …{P}_{{n}} \\ $$$${P}_{{k}} =\left(\mathrm{1}+{kx}\right)^{{k}} =\underset{{r}=\mathrm{0}} {\overset{{k}} {\sum}}{C}_{{r}} ^{{k}} \left({kx}\right)^{{r}} \\ $$$${P}_{{k}} =\mathrm{1}+{k}\left({kx}\right)+\frac{{k}\left({k}−\mathrm{1}\right)}{\mathrm{2}!}\left({kx}\right)^{\mathrm{2}} +\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)}{\mathrm{3}!}\left({kx}\right)^{\mathrm{3}} +\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\left({k}−\mathrm{3}\right)}{\mathrm{4}!}\left({kx}\right)^{\mathrm{4}} +{o}\left({x}^{\mathrm{4}} \right) \\ $$$$=\mathrm{1}+{k}^{\mathrm{2}} {x}+\frac{{k}^{\mathrm{3}} \left({k}−\mathrm{1}\right)}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{{k}^{\mathrm{4}} \left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)}{\mathrm{6}}{x}^{\mathrm{3}} +\frac{{k}^{\mathrm{5}} \left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\left({k}−\mathrm{3}\right)}{\mathrm{24}}{x}^{\mathrm{4}} +{o}\left({x}^{\mathrm{4}} \right) \\ $$$$\Rightarrow{P}_{{k}} =\mathrm{1}+{a}_{{k},\mathrm{1}} {x}+{a}_{{k},\mathrm{2}} {x}^{\mathrm{2}} +{a}_{{k},\mathrm{3}} {x}^{\mathrm{3}} +{a}_{{k},\mathrm{4}} {x}^{\mathrm{4}} +{o}\left({x}^{\mathrm{4}} \right) \\ $$$${with}\: \\ $$$${a}_{\bar {{k}},\mathrm{1}} ={k}^{\mathrm{2}} ,\:{a}_{{k},\mathrm{2}} =\frac{{k}^{\mathrm{3}} \left({k}−\mathrm{1}\right)}{\mathrm{2}},\:{a}_{{k},\mathrm{3}} =\frac{{k}^{\mathrm{4}} \left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)}{\mathrm{6}},\:{a}_{{k},\mathrm{4}} =\frac{{k}^{\mathrm{5}} \left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\left({k}−\mathrm{3}\right)}{\mathrm{24}} \\ $$$${k}=\mathrm{1},\mathrm{2},\mathrm{3},…,{n} \\ $$$$ \\ $$$$\boldsymbol{{coef}}.\:\boldsymbol{{of}}\:\boldsymbol{{x}}\:\boldsymbol{{term}}: \\ $$$${C}_{\mathrm{1}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} =\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$${with}\:{n}=\mathrm{100}, \\ $$$${C}_{\mathrm{1}} =\frac{\mathrm{100}×\mathrm{101}×\mathrm{201}}{\mathrm{6}}=\mathrm{338}\:\mathrm{350} \\ $$$$ \\ $$$$\boldsymbol{{coef}}.\:\boldsymbol{{of}}\:\boldsymbol{{x}}^{\mathrm{2}} \:\boldsymbol{{term}}: \\ $$$${C}_{\mathrm{2}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\underset{{j}={k}+\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} {a}_{{j},\mathrm{1}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} \left(\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{j},\mathrm{1}} −{a}_{{k},\mathrm{1}} \right)+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} \right)^{\mathrm{2}} −\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} ^{\mathrm{2}} \right]+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{\bar {{k}}\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \right)^{\mathrm{2}} −\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{4}} \right]+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{3}} \left({k}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{4}} −\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\right]^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right]^{\mathrm{2}} \\ $$$$=\frac{\left({n}−\mathrm{1}\right){n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} \left({n}+\mathrm{2}\right)}{\mathrm{18}} \\ $$$${with}\:{n}=\mathrm{100}, \\ $$$${C}_{\mathrm{2}} =\frac{\mathrm{99}×\mathrm{100}^{\mathrm{2}} ×\mathrm{101}^{\mathrm{2}} ×\mathrm{102}}{\mathrm{18}}=\mathrm{57}\:\mathrm{227}\:\mathrm{610}\:\mathrm{000} \\ $$$$ \\ $$$$\left({to}\:{be}\:{continued}\right) \\ $$
Commented by TawaTawa1 last updated on 26/Mar/20
Sweet, i will study this, God bless you sir
$$\mathrm{Sweet},\:\mathrm{i}\:\mathrm{will}\:\mathrm{study}\:\mathrm{this},\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by TawaTawa1 last updated on 26/Mar/20
Sir, your method too is needed in Q85950.
$$\mathrm{Sir},\:\mathrm{your}\:\mathrm{method}\:\mathrm{too}\:\mathrm{is}\:\mathrm{needed}\:\mathrm{in}\:\:\mathrm{Q85950}. \\ $$
Commented by Prithwish Sen 1 last updated on 26/Mar/20
excellent sir.
$$\mathrm{excellent}\:\mathrm{sir}. \\ $$
Commented by Prithwish Sen 1 last updated on 26/Mar/20
sir think I get it for x^3 . Please comment.
$$\mathrm{sir}\:\mathrm{think}\:\mathrm{I}\:\mathrm{get}\:\mathrm{it}\:\mathrm{for}\:\mathrm{x}^{\mathrm{3}} .\:\mathrm{Please}\:\mathrm{comment}. \\ $$
Commented by Prithwish Sen 1 last updated on 27/Mar/20
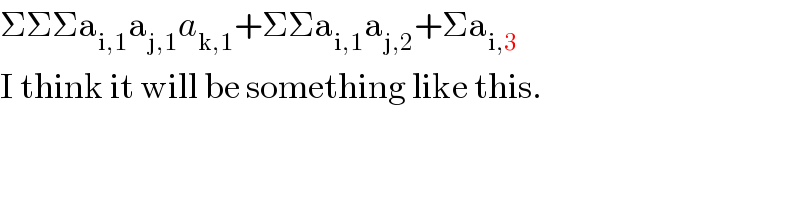
ΣΣΣa_(i,1) a_(j,1) a_(k,1) +ΣΣa_(i,1) a_(j,2) +Σa_(i,3) I think it will be something like this.
$$\Sigma\Sigma\Sigma\mathrm{a}_{\mathrm{i},\mathrm{1}} \mathrm{a}_{\mathrm{j},\mathrm{1}} {a}_{\mathrm{k},\mathrm{1}} +\Sigma\Sigma\mathrm{a}_{\mathrm{i},\mathrm{1}} \mathrm{a}_{\mathrm{j},\mathrm{2}} +\Sigma\mathrm{a}_{\mathrm{i},\mathrm{3}} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be}\:\mathrm{something}\:\mathrm{like}\:\mathrm{this}. \\ $$
Commented by Prithwish Sen 1 last updated on 26/Mar/20
I think u bave missed the product of a_(i,1) .a_(j,1) .a_(k,1)
$$\mathrm{I}\:\mathrm{think}\:\mathrm{u}\:\mathrm{bave}\:\mathrm{missed}\:\:\mathrm{the}\:\mathrm{product}\:\mathrm{of}\: \\ $$$$\mathrm{a}_{\mathrm{i},\mathrm{1}} .\mathrm{a}_{\mathrm{j},\mathrm{1}} .\mathrm{a}_{\mathrm{k},\mathrm{1}} \\ $$
Commented by mr W last updated on 05/Apr/20
(continued) let K_2 =Σ_(k=1) ^n k^2 =((n(n+1)(2n+1))/6) K_3 =Σ_(k=1) ^n k^3 =((n^2 (n+1)^2 )/4) K_4 =Σ_(k=1) ^n k^4 =((n(n+1)(2n+1)(3n^2 +3n−1))/(30))=((3n^2 +3n−1)/5)K_2 K_5 =Σ_(k=1) ^n k^5 =((n^2 (n+1)^2 (2n^2 +2n−1))/(12))=((2n^2 +2n−1)/3)K_3 K_6 =Σ_(k=1) ^n k^6 =((n(n+1)(2n+1)(3n^4 +6n^3 −3n+1))/(42))=((3n^4 +6n^3 −3n+1)/7)K_2 coef. of x^3 term: C_3 =C_(31) +C_(32) +C_(33) with C_(31) =Σ_(k≠j≠i) ^n a_(k,1) a_(j,1) a_(i,1) C_(32) =Σ_(k,j=1,j≠k) ^n a_(k,1) a_(j,2) C_(33) =Σ_(k=1) ^n a_(k,3) C_(31) =(1/6)[(Σ_(k=1) ^n a_(k,1) )^3 −Σ_(k=1) ^n a_(k,1) ^3 −3Σ_(i=1) ^n a_(i,1) ^2 (Σ_(k=1) ^n a_(k,1) −a_(i,1) )] =(1/6)[(Σ_(k=1) ^n a_(k,1) )^3 −Σ_(k=1) ^n a_(k,1) ^3 −3(Σ_(i=1) ^n a_(i,1) ^2 )(Σ_(k=1) ^n a_(k,1) )+3Σ_(i=1) ^n a_(i,1) ^3 ] =(1/6)(K_2 ^3 −3K_4 K_2 +2K_6 ) C_(32) =Σ_(k=1) ^n a_(k,1) Σ_(j=1,j≠k) ^n a_(j,2) =Σ_(k=1) ^n a_(k,1) (Σ_(j=1) ^n a_(j,2) −a_(k,2) ) =(Σ_(k=1) ^n a_(k,1) )(Σ_(j=1) ^n a_(j,2) )−Σ_(k=1) ^n a_(k,1) a_(k,2) =(Σ_(k=1) ^n k^2 )(Σ_(k=1) ^n ((k^3 (k−1))/2))−Σ_(k=1) ^n ((k^2 k^3 (k−1))/2) =(1/2)(K_2 K_4 −K_2 K_3 −K_6 +K_5 ) C_(33) =Σ_(k=1) ^n a_(k,3) =Σ_(k=1) ^n ((k^4 (k−1)(k−2))/6) =(1/6)(K_6 −3K_5 +2K_4 ) C_3 =(1/6)(K_2 ^3 −3K_2 K_4 +2K_6 )+(1/2)(K_2 K_4 −K_2 K_3 −K_6 +K_5 )+(1/6)(K_6 −3K_5 +2K_4 ) =(1/6)(K_2 ^3 −3K_2 K_3 +2K_4 ) =((n(n+1)(2n+1))/(36))[((n^2 (n+1)^2 (2n+1)^2 )/(36))−((3n^2 (n+1)^2 )/4)+((2(3n^2 +3n−1))/5)] =((n(n+1)(2n+1))/(36))[((n^2 (n+1)^2 (2n^2 +2n−13))/(18))+((2(3n^2 +3n−1))/5)] =(((n−1)n(n+1)(n+2)(2n+1)(10n^4 +20n^3 −35n^2 −45n+18))/(3240)) with n=100, C_3 =((99×100×101×102×201×(10×100^4 +20×10^3 −35×100^2 −45×100+18))/(3240)) =6 451 445 040 986 110
$$\left({continued}\right) \\ $$$$ \\ $$$${let} \\ $$$${K}_{\mathrm{2}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} =\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$${K}_{\mathrm{3}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{3}} =\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$${K}_{\mathrm{4}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{4}} =\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{1}\right)}{\mathrm{30}}=\frac{\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{1}}{\mathrm{5}}{K}_{\mathrm{2}} \\ $$$${K}_{\mathrm{5}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{5}} =\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{12}}=\frac{\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}−\mathrm{1}}{\mathrm{3}}{K}_{\mathrm{3}} \\ $$$${K}_{\mathrm{6}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{6}} =\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}^{\mathrm{4}} +\mathrm{6}{n}^{\mathrm{3}} −\mathrm{3}{n}+\mathrm{1}\right)}{\mathrm{42}}=\frac{\mathrm{3}{n}^{\mathrm{4}} +\mathrm{6}{n}^{\mathrm{3}} −\mathrm{3}{n}+\mathrm{1}}{\mathrm{7}}{K}_{\mathrm{2}} \\ $$$$ \\ $$$$\boldsymbol{{coef}}.\:\boldsymbol{{of}}\:\boldsymbol{{x}}^{\mathrm{3}} \:\boldsymbol{{term}}: \\ $$$${C}_{\mathrm{3}} ={C}_{\mathrm{31}} +{C}_{\mathrm{32}} +{C}_{\mathrm{33}} \\ $$$${with} \\ $$$${C}_{\mathrm{31}} =\underset{{k}\neq{j}\neq{i}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} {a}_{{j},\mathrm{1}} {a}_{{i},\mathrm{1}} \\ $$$${C}_{\mathrm{32}} =\underset{{k},{j}=\mathrm{1},{j}\neq{k}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} {a}_{{j},\mathrm{2}} \\ $$$${C}_{\mathrm{33}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{3}} \\ $$$$ \\ $$$${C}_{\mathrm{31}} =\frac{\mathrm{1}}{\mathrm{6}}\left[\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} \right)^{\mathrm{3}} −\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} ^{\mathrm{3}} −\mathrm{3}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i},\mathrm{1}} ^{\mathrm{2}} \left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} −{a}_{{i},\mathrm{1}} \right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} \right)^{\mathrm{3}} −\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} ^{\mathrm{3}} −\mathrm{3}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i},\mathrm{1}} ^{\mathrm{2}} \right)\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} \right)+\mathrm{3}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i},\mathrm{1}} ^{\mathrm{3}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left({K}_{\mathrm{2}} ^{\mathrm{3}} −\mathrm{3}{K}_{\mathrm{4}} {K}_{\mathrm{2}} +\mathrm{2}{K}_{\mathrm{6}} \right) \\ $$$$ \\ $$$${C}_{\mathrm{32}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} \underset{{j}=\mathrm{1},{j}\neq{k}} {\overset{{n}} {\sum}}{a}_{{j},\mathrm{2}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} \left(\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{j},\mathrm{2}} −{a}_{{k},\mathrm{2}} \right) \\ $$$$=\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} \right)\left(\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{j},\mathrm{2}} \right)−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} {a}_{{k},\mathrm{2}} \\ $$$$=\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \right)\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{3}} \left({k}−\mathrm{1}\right)}{\mathrm{2}}\right)−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{2}} {k}^{\mathrm{3}} \left({k}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({K}_{\mathrm{2}} {K}_{\mathrm{4}} −{K}_{\mathrm{2}} {K}_{\mathrm{3}} −{K}_{\mathrm{6}} +{K}_{\mathrm{5}} \right) \\ $$$$ \\ $$$${C}_{\mathrm{33}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{3}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{4}} \left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)}{\mathrm{6}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left({K}_{\mathrm{6}} −\mathrm{3}{K}_{\mathrm{5}} +\mathrm{2}{K}_{\mathrm{4}} \right) \\ $$$$ \\ $$$${C}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{6}}\left({K}_{\mathrm{2}} ^{\mathrm{3}} −\mathrm{3}{K}_{\mathrm{2}} {K}_{\mathrm{4}} +\mathrm{2}{K}_{\mathrm{6}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\left({K}_{\mathrm{2}} {K}_{\mathrm{4}} −{K}_{\mathrm{2}} {K}_{\mathrm{3}} −{K}_{\mathrm{6}} +{K}_{\mathrm{5}} \right)+\frac{\mathrm{1}}{\mathrm{6}}\left({K}_{\mathrm{6}} −\mathrm{3}{K}_{\mathrm{5}} +\mathrm{2}{K}_{\mathrm{4}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left({K}_{\mathrm{2}} ^{\mathrm{3}} −\mathrm{3}{K}_{\mathrm{2}} {K}_{\mathrm{3}} +\mathrm{2}{K}_{\mathrm{4}} \right) \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{36}}\left[\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{36}}−\frac{\mathrm{3}{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{2}\left(\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{1}\right)}{\mathrm{5}}\right] \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{36}}\left[\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}−\mathrm{13}\right)}{\mathrm{18}}+\frac{\mathrm{2}\left(\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{1}\right)}{\mathrm{5}}\right] \\ $$$$=\frac{\left({n}−\mathrm{1}\right){n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{10}{n}^{\mathrm{4}} +\mathrm{20}{n}^{\mathrm{3}} −\mathrm{35}{n}^{\mathrm{2}} −\mathrm{45}{n}+\mathrm{18}\right)}{\mathrm{3240}} \\ $$$${with}\:{n}=\mathrm{100}, \\ $$$${C}_{\mathrm{3}} =\frac{\mathrm{99}×\mathrm{100}×\mathrm{101}×\mathrm{102}×\mathrm{201}×\left(\mathrm{10}×\mathrm{100}^{\mathrm{4}} +\mathrm{20}×\mathrm{10}^{\mathrm{3}} −\mathrm{35}×\mathrm{100}^{\mathrm{2}} −\mathrm{45}×\mathrm{100}+\mathrm{18}\right)}{\mathrm{3240}} \\ $$$$=\mathrm{6}\:\mathrm{451}\:\mathrm{445}\:\mathrm{040}\:\mathrm{986}\:\mathrm{110} \\ $$
Commented by Prithwish Sen 1 last updated on 27/Mar/20
Thank you sir.I fix it sir.
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\mathrm{I}\:\mathrm{fix}\:\mathrm{it}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 06/Apr/20
coef. of x^4 term: C_4 =C_(41) +C_(42) +C_(43) +C_(44) +C_(45) with C_(41) =Σ_(k≠i≠j≠h) a_(k,1) a_(i,1) a_(j,1) a_(h,1) C_(42) =Σ_(k≠i≠j) a_(k,1) a_(i,1) a_(j,2) C_(43) =Σ_(k≠i) a_(k,1) a_(i,3) C_(44) =Σ_(k≠i) a_(k,2) a_(i,2) C_(45) =Σ_(k=1) ^n a_(k,4) ..... C_(42) =Σ_(k≠i≠j) a_(k,1) a_(i,1) a_(j,2) C_(43) =Σ_(k≠i) a_(k,1) a_(i,3) =(1/2)Σ_(k=1) ^n a_(k,1) (Σ_(i=1) ^n a_(i,3) −a_(k,3) ) =(1/2)[(Σ_(k=1) ^n a_(k,1) )(Σ_(i=1) ^n a_(i,3) )−Σ_(k=1) ^n a_(k,1) a_(k,3) ] =(1/2)[(Σ_(k=1) ^n k^2 )(Σ_(i=1) ^n ((k^4 (k−1)(k−2))/6))−Σ_(k=1) ^n ((k^6 (k−1))k−2))/6)] =(1/(12))[(Σ_(k=1) ^n k^2 )(Σ_(i=1) ^n k^4 (k−1)(k−2))−Σ_(k=1) ^n k^6 (k−1)(k−2)] =(1/(12))[(Σ_(k=1) ^n k^2 )(Σ_(i=1) ^n (k^6 −3k^5 +2k^4 ))−Σ_(k=1) ^n (k^8 −3k^7 +2k^6 )] =(1/(12))[K_2 (K_6 −3K_5 +2K_4 )−(K_8 −3K_7 +2K_6 )] =(1/(12))(K_2 K_6 −3K_2 K_5 +2K_2 K_4 −K_8 +3K_7 −2K_6 ) C_(44) =Σ_(k≠i) a_(k,2) a_(i,2) =(1/2)Σ_(k=1) ^n a_(k,2) (Σ_(i=1) ^n a_(i,2) −a_(k,2) ) =(1/2)[(Σ_(k=1) ^n a_(k,2) )^2 −Σ_(k=1) ^n a_(k,2) ^2 ] =(1/2)[(Σ_(k=1) ^n ((k^3 (k−1))/2))^2 −Σ_(k=1) ^n ((k^6 (k−1)^2 )/4)] =(1/8)[(K_4 −K_3 )^2 −(K_8 −2K_7 +K_6 )] =(1/8)(K_4 ^2 −2K_3 K_4 +K_3 ^2 −K_8 +2K_7 −K_6 ) C_(45) =Σ_(k=1) ^n a_(k,4) =Σ_(k=1) ^n ((k^5 (k−1)(k−2)(k−3))/(24)) =(1/(24))(K_8 −6K_7 +11K_6 −6K_5 ) ......
$$\boldsymbol{{coef}}.\:\boldsymbol{{of}}\:\boldsymbol{{x}}^{\mathrm{4}} \:\boldsymbol{{term}}: \\ $$$$ \\ $$$${C}_{\mathrm{4}} ={C}_{\mathrm{41}} +{C}_{\mathrm{42}} +{C}_{\mathrm{43}} +{C}_{\mathrm{44}} +{C}_{\mathrm{45}} \\ $$$${with} \\ $$$${C}_{\mathrm{41}} =\underset{{k}\neq{i}\neq{j}\neq{h}} {\sum}{a}_{{k},\mathrm{1}} {a}_{{i},\mathrm{1}} {a}_{{j},\mathrm{1}} {a}_{{h},\mathrm{1}} \\ $$$${C}_{\mathrm{42}} =\underset{{k}\neq{i}\neq{j}} {\sum}{a}_{{k},\mathrm{1}} {a}_{{i},\mathrm{1}} {a}_{{j},\mathrm{2}} \\ $$$${C}_{\mathrm{43}} =\underset{{k}\neq{i}} {\sum}{a}_{{k},\mathrm{1}} {a}_{{i},\mathrm{3}} \\ $$$${C}_{\mathrm{44}} =\underset{{k}\neq{i}} {\sum}{a}_{{k},\mathrm{2}} {a}_{{i},\mathrm{2}} \\ $$$${C}_{\mathrm{45}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{4}} \\ $$$$….. \\ $$$${C}_{\mathrm{42}} =\underset{{k}\neq{i}\neq{j}} {\sum}{a}_{{k},\mathrm{1}} {a}_{{i},\mathrm{1}} {a}_{{j},\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$${C}_{\mathrm{43}} =\underset{{k}\neq{i}} {\sum}{a}_{{k},\mathrm{1}} {a}_{{i},\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} \left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i},\mathrm{3}} −{a}_{{k},\mathrm{3}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} \right)\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i},\mathrm{3}} \right)−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{1}} {a}_{{k},\mathrm{3}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \right)\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{4}} \left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)}{\mathrm{6}}\right)−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left.{k}^{\mathrm{6}} \left.\left({k}−\mathrm{1}\right)\right){k}−\mathrm{2}\right)}{\mathrm{6}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left[\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \right)\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{4}} \left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\right)−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{6}} \left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left[\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \right)\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left({k}^{\mathrm{6}} −\mathrm{3}{k}^{\mathrm{5}} +\mathrm{2}{k}^{\mathrm{4}} \right)\right)−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({k}^{\mathrm{8}} −\mathrm{3}{k}^{\mathrm{7}} +\mathrm{2}{k}^{\mathrm{6}} \right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left[{K}_{\mathrm{2}} \left({K}_{\mathrm{6}} −\mathrm{3}{K}_{\mathrm{5}} +\mathrm{2}{K}_{\mathrm{4}} \right)−\left({K}_{\mathrm{8}} −\mathrm{3}{K}_{\mathrm{7}} +\mathrm{2}{K}_{\mathrm{6}} \right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left({K}_{\mathrm{2}} {K}_{\mathrm{6}} −\mathrm{3}{K}_{\mathrm{2}} {K}_{\mathrm{5}} +\mathrm{2}{K}_{\mathrm{2}} {K}_{\mathrm{4}} −{K}_{\mathrm{8}} +\mathrm{3}{K}_{\mathrm{7}} −\mathrm{2}{K}_{\mathrm{6}} \right) \\ $$$$ \\ $$$${C}_{\mathrm{44}} =\underset{{k}\neq{i}} {\sum}{a}_{{k},\mathrm{2}} {a}_{{i},\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{2}} \left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i},\mathrm{2}} −{a}_{{k},\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{2}} \right)^{\mathrm{2}} −\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{2}} ^{\mathrm{2}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{3}} \left({k}−\mathrm{1}\right)}{\mathrm{2}}\right)^{\mathrm{2}} −\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{6}} \left({k}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left[\left({K}_{\mathrm{4}} −{K}_{\mathrm{3}} \right)^{\mathrm{2}} −\left({K}_{\mathrm{8}} −\mathrm{2}{K}_{\mathrm{7}} +{K}_{\mathrm{6}} \right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left({K}_{\mathrm{4}} ^{\mathrm{2}} −\mathrm{2}{K}_{\mathrm{3}} {K}_{\mathrm{4}} +{K}_{\mathrm{3}} ^{\mathrm{2}} −{K}_{\mathrm{8}} +\mathrm{2}{K}_{\mathrm{7}} −{K}_{\mathrm{6}} \right) \\ $$$$ \\ $$$${C}_{\mathrm{45}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k},\mathrm{4}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{5}} \left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)\left({k}−\mathrm{3}\right)}{\mathrm{24}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}\left({K}_{\mathrm{8}} −\mathrm{6}{K}_{\mathrm{7}} +\mathrm{11}{K}_{\mathrm{6}} −\mathrm{6}{K}_{\mathrm{5}} \right) \\ $$$$…… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *