Question Number 57821 by behi83417@gmail.com last updated on 12/Apr/19

$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{common}}\:\boldsymbol{\mathrm{area}}\:\boldsymbol{\mathrm{of}}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{cases}{\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{3}}+\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\mathrm{1}}\\{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\frac{\boldsymbol{\mathrm{y}}^{\mathrm{2}} }{\mathrm{3}}=\mathrm{1}}\end{cases} \\ $$
Answered by MJS last updated on 13/Apr/19
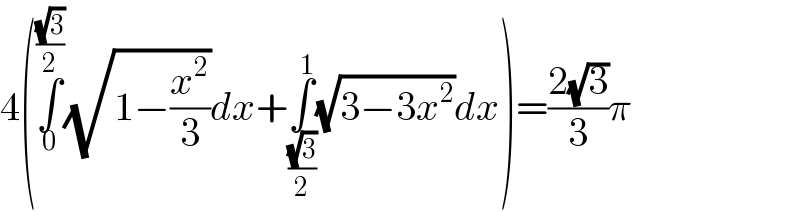
$$\mathrm{4}\left(\underset{\mathrm{0}} {\overset{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} {\int}}\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}{dx}+\underset{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{3}−\mathrm{3}{x}^{\mathrm{2}} }{dx}\right)=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\pi \\ $$
Answered by mr W last updated on 13/Apr/19
![r^2 =((a^2 b^2 )/(b^2 cos^2 θ+a^2 sin^2 θ)) A_(common) =8∫_0 ^(π/4) ((r^2 dθ)/2)=4a^2 b^2 ∫_0 ^(π/4) (dθ/(b^2 cos^2 θ+a^2 sin^2 θ)) =4ab[tan^(−1) ((a/b)tan θ)]_0 ^(π/4) =4ab tan^(−1) ((a/b)) with a=1, b=(√3) A_(common) =4(√3) tan^(−1) ((1/( (√3))))=((4(√3)π)/6)=((2(√3)π)/3)](https://www.tinkutara.com/question/Q57829.png)
$${r}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$${A}_{{common}} =\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{r}^{\mathrm{2}} {d}\theta}{\mathrm{2}}=\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\theta}{{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$=\mathrm{4}{ab}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}}{{b}}\mathrm{tan}\:\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\mathrm{4}{ab}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}}{{b}}\right) \\ $$$${with}\:{a}=\mathrm{1},\:{b}=\sqrt{\mathrm{3}} \\ $$$${A}_{{common}} =\mathrm{4}\sqrt{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)=\frac{\mathrm{4}\sqrt{\mathrm{3}}\pi}{\mathrm{6}}=\frac{\mathrm{2}\sqrt{\mathrm{3}}\pi}{\mathrm{3}} \\ $$
Commented by behi83417@gmail.com last updated on 13/Apr/19
$${thank}\:{you}\:{so}\:{much}\:{sir}\:{MJS}\:{and}\:{sir}\:{MrW}. \\ $$
