Question Number 30123 by tawa tawa last updated on 16/Feb/18
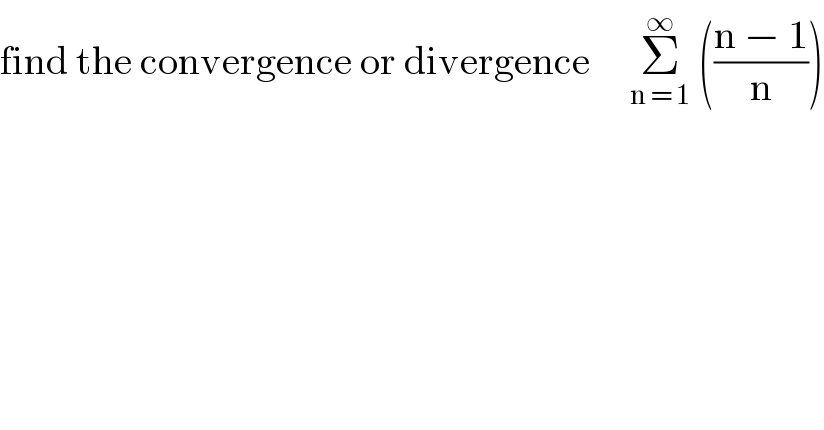
$$\mathrm{find}\:\mathrm{the}\:\mathrm{convergence}\:\mathrm{or}\:\mathrm{divergence}\:\:\:\:\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{n}\:−\:\mathrm{1}}{\mathrm{n}}\right) \\ $$
Commented by prof Abdo imad last updated on 16/Feb/18
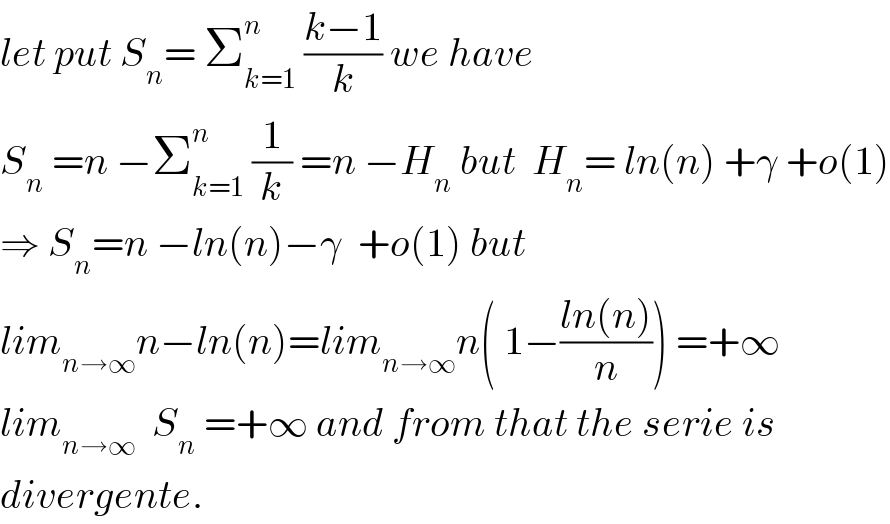
$${let}\:{put}\:{S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}−\mathrm{1}}{{k}}\:{we}\:{have} \\ $$$${S}_{{n}} \:={n}\:−\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:={n}\:−{H}_{{n}} \:{but}\:\:{H}_{{n}} =\:{ln}\left({n}\right)\:+\gamma\:+{o}\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:{S}_{{n}} ={n}\:−{ln}\left({n}\right)−\gamma\:\:+{o}\left(\mathrm{1}\right)\:{but} \\ $$$${lim}_{{n}\rightarrow\infty} {n}−{ln}\left({n}\right)={lim}_{{n}\rightarrow\infty} {n}\left(\:\mathrm{1}−\frac{{ln}\left({n}\right)}{{n}}\right)\:=+\infty \\ $$$${lim}_{{n}\rightarrow\infty} \:\:{S}_{{n}} \:=+\infty\:{and}\:{from}\:{that}\:{the}\:{serie}\:{is} \\ $$$${divergente}. \\ $$
Commented by tawa tawa last updated on 17/Feb/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by abdo imad last updated on 17/Feb/18

$${many}\:{thanks}\:{sir}\:{tawa}\:{tawa}… \\ $$
