Find-the-coordinates-of-the-point-on-the-curve-y-3x-2-2x-5-where-the-tangent-is-parallel-to-the-line-y-5-8x-

Question Number 167567 by pete last updated on 19/Mar/22

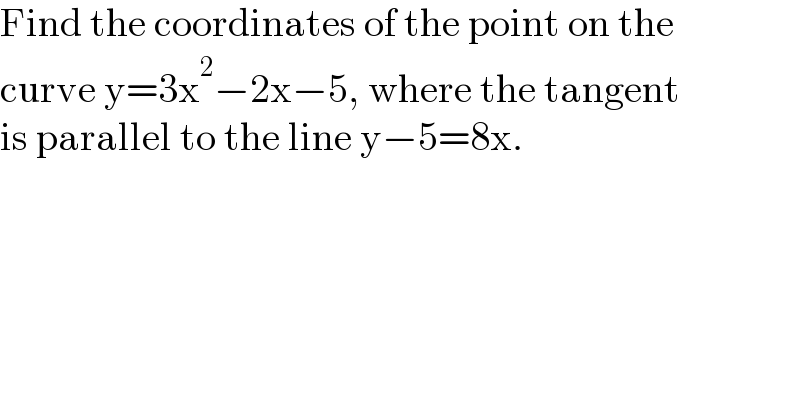
Find the coordinates of the point on the

curve y = {3 x}^{2} - 2 x - 5, where the tangent

is parallel to the line y - 5 = 8 x .

Commented by greogoury55 last updated on 19/Mar/22

y^{'} = 8

6 x - 2 = 8 \Rightarrow x = \frac{5}{3}

y = 3 (\frac{25}{9}) - 2 (\frac{5}{3}) - 5

y = \frac{25 - 10 - 15}{3} = 0

t h e p o i n t (\frac{5}{3}, 0)

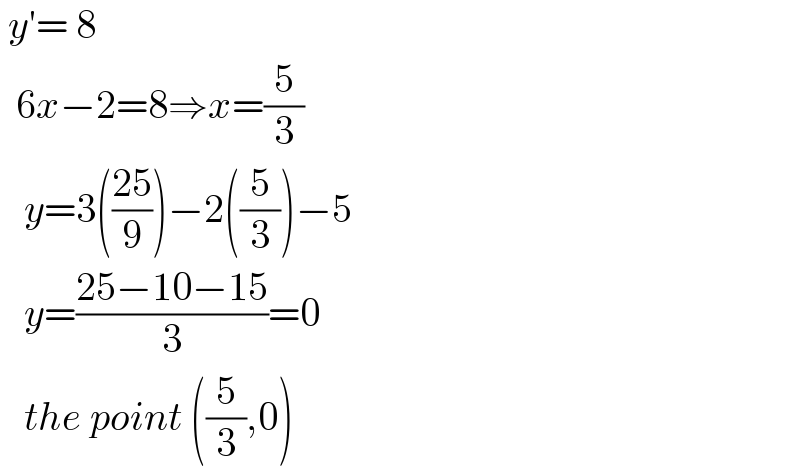
Commented by pete last updated on 19/Mar/22

Thanks for your time, sir

Commented by otchereabdullai@gmail.com last updated on 21/Mar/22

nice!

Answered by som(math1967) last updated on 19/Mar/22

s l o p e o f y = 8 x + 5 i s 8

∴ s l o p e o f t a n g e n t a l s o 8

n o w y = 3 x^{2} - 2 x - 5

\frac{d y}{d x} = 6 x - 2 ∴ 6 x - 2 = 8 \Rightarrow x = \frac{10}{6} = \frac{5}{3}

∴ y = 3 \times \frac{25}{9} - \frac{10}{3} - 5 = 5 - 5 = 0

∴ p o i n t i s (\frac{5}{3}, 0)

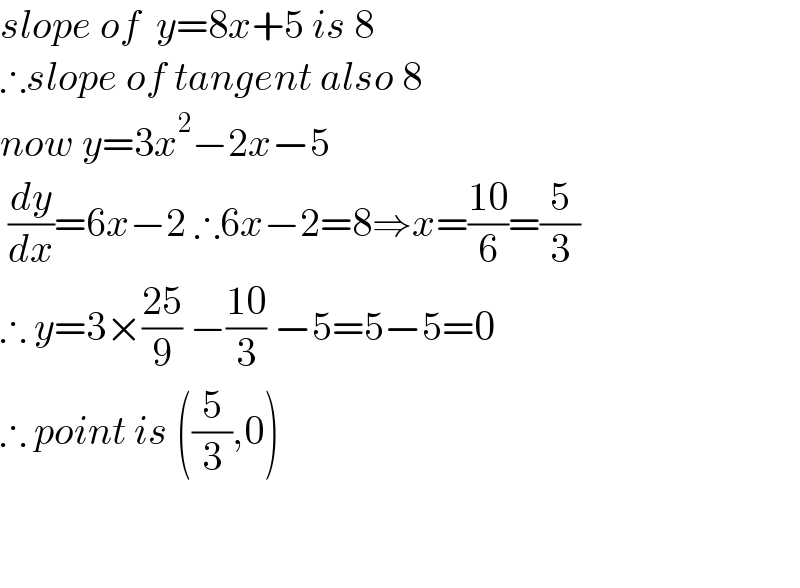
Commented by pete last updated on 19/Mar/22

thank you sir

Facebook Tweet Pin