Question Number 156105 by zainaltanjung last updated on 08/Oct/21
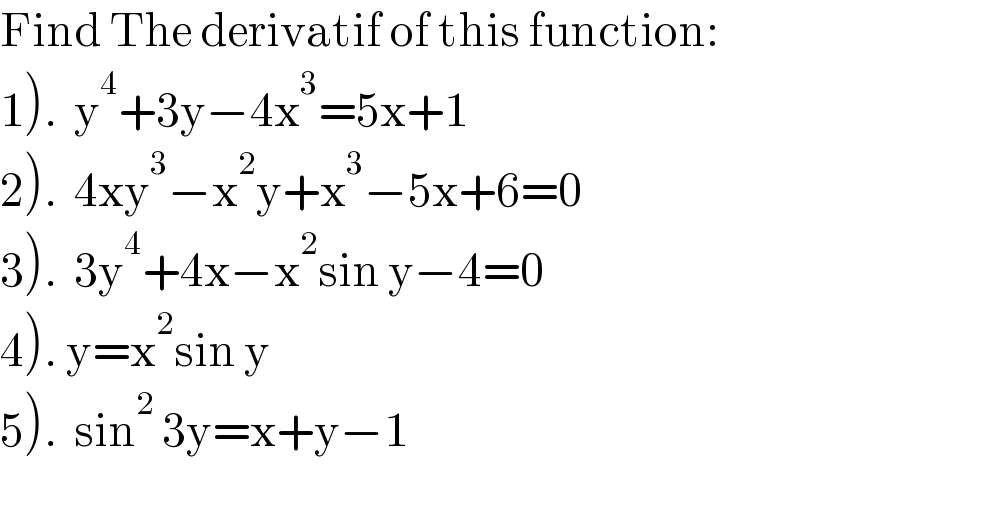
$$\mathrm{Find}\:\mathrm{The}\:\mathrm{derivatif}\:\mathrm{of}\:\mathrm{this}\:\mathrm{function}: \\ $$$$\left.\mathrm{1}\right).\:\:\mathrm{y}^{\mathrm{4}} +\mathrm{3y}−\mathrm{4x}^{\mathrm{3}} =\mathrm{5x}+\mathrm{1} \\ $$$$\left.\mathrm{2}\right).\:\:\mathrm{4xy}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{x}^{\mathrm{3}} −\mathrm{5x}+\mathrm{6}=\mathrm{0} \\ $$$$\left.\mathrm{3}\right).\:\:\mathrm{3y}^{\mathrm{4}} +\mathrm{4x}−\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:\mathrm{y}−\mathrm{4}=\mathrm{0} \\ $$$$\left.\mathrm{4}\right).\:\mathrm{y}=\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:\mathrm{y} \\ $$$$\left.\mathrm{5}\right).\:\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{3y}=\mathrm{x}+\mathrm{y}−\mathrm{1} \\ $$$$\: \\ $$
Answered by MathsFan last updated on 08/Oct/21
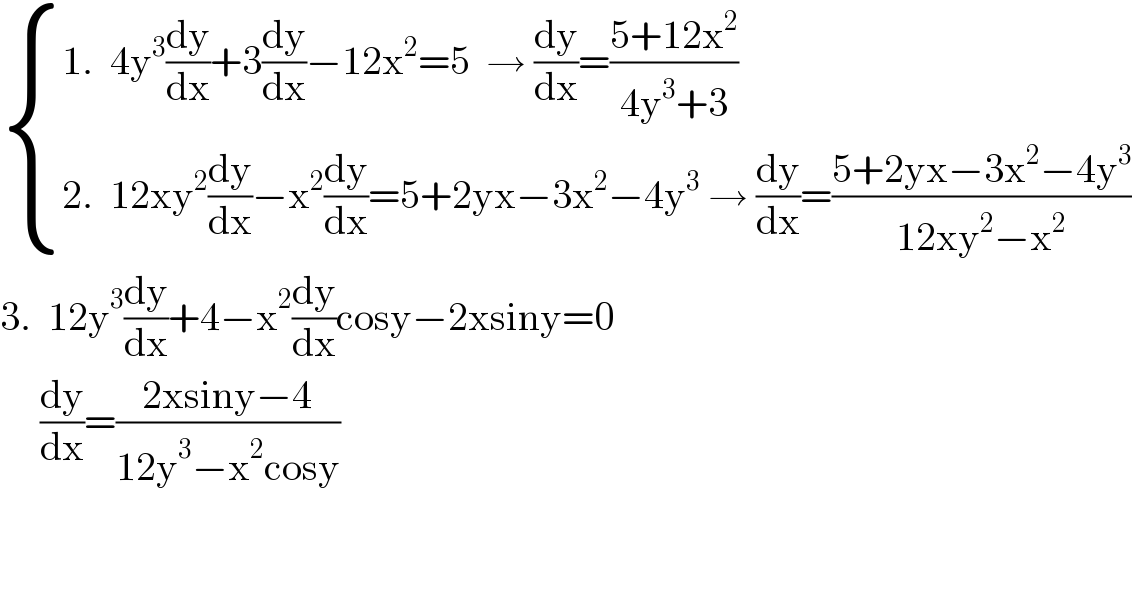
$$\begin{cases}{\mathrm{1}.\:\:\mathrm{4y}^{\mathrm{3}} \frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{3}\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{12x}^{\mathrm{2}} =\mathrm{5}\:\:\rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{5}+\mathrm{12x}^{\mathrm{2}} }{\mathrm{4y}^{\mathrm{3}} +\mathrm{3}}}\\{\mathrm{2}.\:\:\mathrm{12xy}^{\mathrm{2}} \frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{x}^{\mathrm{2}} \frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{5}+\mathrm{2yx}−\mathrm{3x}^{\mathrm{2}} −\mathrm{4y}^{\mathrm{3}} \:\rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{5}+\mathrm{2yx}−\mathrm{3x}^{\mathrm{2}} −\mathrm{4y}^{\mathrm{3}} }{\mathrm{12xy}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }}\end{cases} \\ $$$$\mathrm{3}.\:\:\mathrm{12y}^{\mathrm{3}} \frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{4}−\mathrm{x}^{\mathrm{2}} \frac{\mathrm{dy}}{\mathrm{dx}}\mathrm{cosy}−\mathrm{2xsiny}=\mathrm{0} \\ $$$$\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{2xsiny}−\mathrm{4}}{\mathrm{12y}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} \mathrm{cosy}} \\ $$$$ \\ $$$$ \\ $$
