Question Number 24913 by chernoaguero@gmail.com last updated on 28/Nov/17
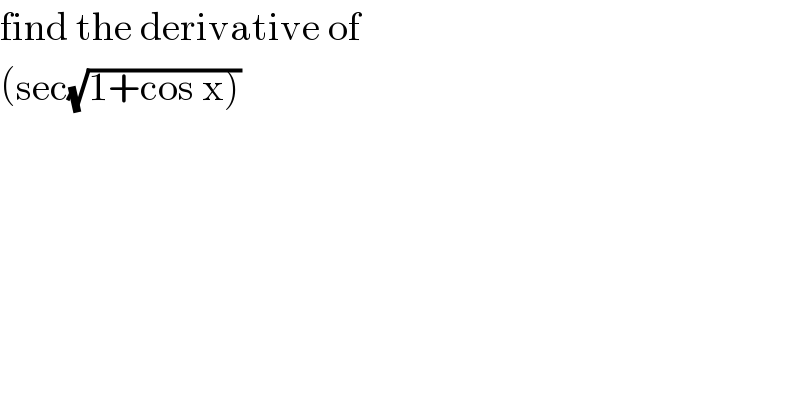
$$\mathrm{find}\:\mathrm{the}\:\mathrm{derivative}\:\mathrm{of} \\ $$$$\left(\mathrm{sec}\sqrt{\left.\mathrm{1}+\mathrm{cos}\:\mathrm{x}\right)}\right. \\ $$
Commented by prakash jain last updated on 28/Nov/17
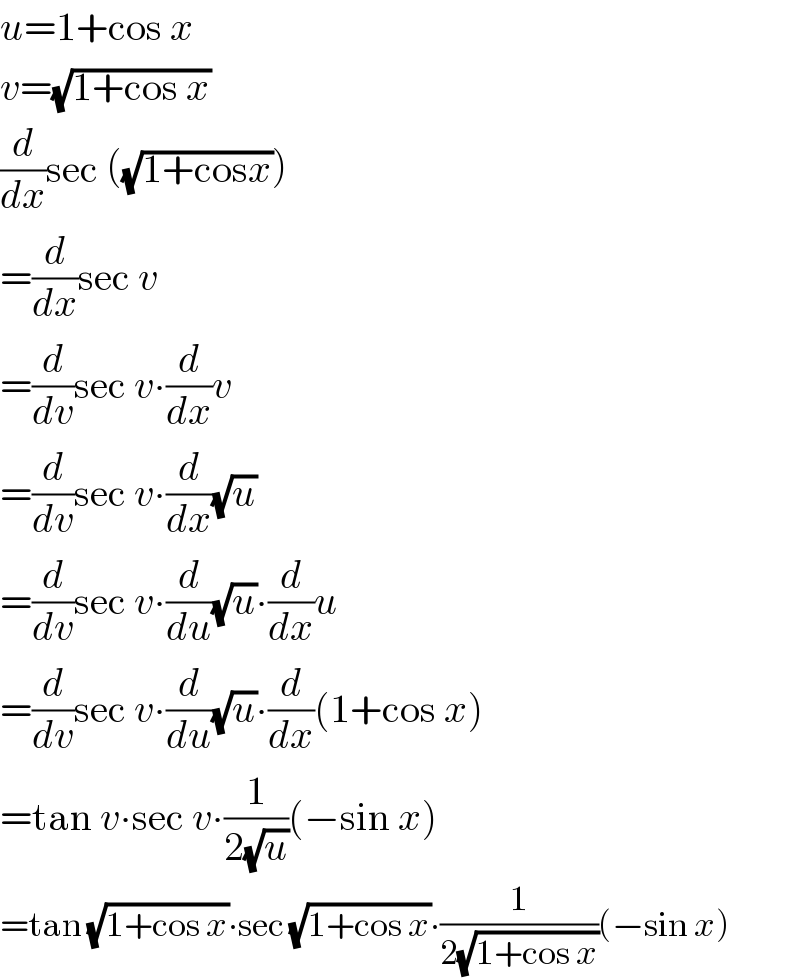
$${u}=\mathrm{1}+\mathrm{cos}\:{x} \\ $$$${v}=\sqrt{\mathrm{1}+\mathrm{cos}\:{x}} \\ $$$$\frac{{d}}{{dx}}\mathrm{sec}\:\left(\sqrt{\mathrm{1}+\mathrm{cos}{x}}\right) \\ $$$$=\frac{{d}}{{dx}}\mathrm{sec}\:{v} \\ $$$$=\frac{{d}}{{dv}}\mathrm{sec}\:{v}\centerdot\frac{{d}}{{dx}}{v} \\ $$$$=\frac{{d}}{{dv}}\mathrm{sec}\:{v}\centerdot\frac{{d}}{{dx}}\sqrt{{u}} \\ $$$$=\frac{{d}}{{dv}}\mathrm{sec}\:{v}\centerdot\frac{{d}}{{du}}\sqrt{{u}}\centerdot\frac{{d}}{{dx}}{u} \\ $$$$=\frac{{d}}{{dv}}\mathrm{sec}\:{v}\centerdot\frac{{d}}{{du}}\sqrt{{u}}\centerdot\frac{{d}}{{dx}}\left(\mathrm{1}+\mathrm{cos}\:{x}\right) \\ $$$$=\mathrm{tan}\:{v}\centerdot\mathrm{sec}\:{v}\centerdot\frac{\mathrm{1}}{\mathrm{2}\sqrt{{u}}}\left(−\mathrm{sin}\:{x}\right) \\ $$$$=\mathrm{tan}\:\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}\centerdot\mathrm{sec}\:\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}\centerdot\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}}\left(−\mathrm{sin}\:{x}\right) \\ $$
Commented by chernoaguero@gmail.com last updated on 28/Nov/17

$$\mathrm{Thank}\:\mathrm{alot}\:\:\mathrm{sir} \\ $$$$ \\ $$
