find-the-derivtive-of-y-10-x-log-10-x-

Question Number 83257 by 09658867628 last updated on 29/Feb/20

f i n d t h e d e r i v t i v e o f y = \frac{10^{x}}{{l o g}_{10} x}

Answered by TANMAY PANACEA last updated on 29/Feb/20

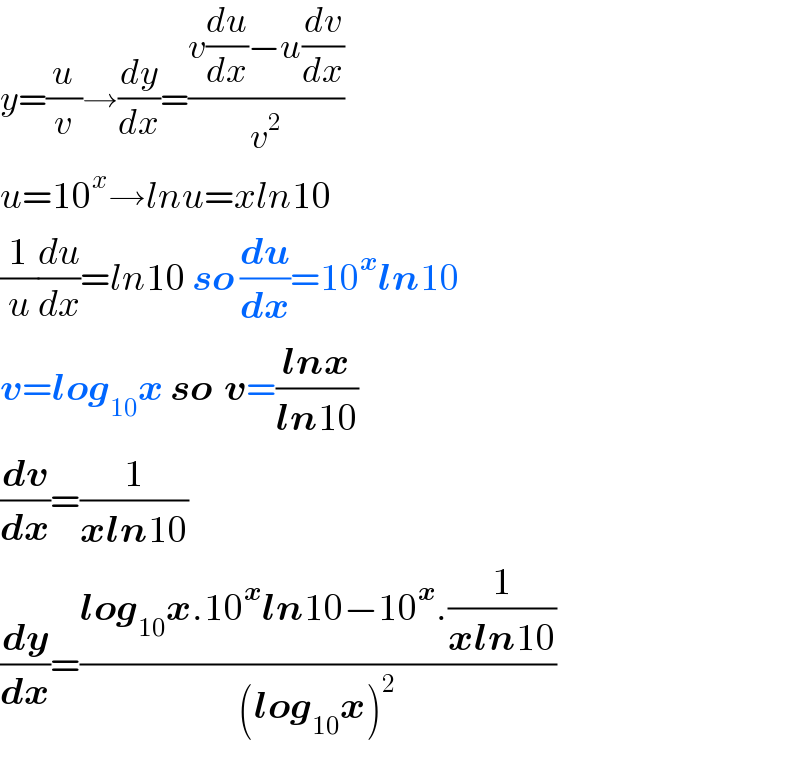
y = \frac{u}{v} \to \frac{d y}{d x} = \frac{v \frac{d u}{d x} - u \frac{d v}{d x}}{v^{2}}

u = 10^{x} \to l n u = x l n 10

\frac{1}{u} \frac{d u}{d x} = l n 10 s o \frac{d u}{d x} = 10^{x} l n 10

v = {l o g}_{10} x s o v = \frac{l n x}{l n 10}

\frac{d v}{d x} = \frac{1}{x l n 10}

\frac{d y}{d x} = \frac{{l o g}_{10} x . 10^{x} l n 10 - 10^{x} . \frac{1}{x l n 10}}{{({l o g}_{10} x)}^{2}}