Question Number 83156 by 09658867628 last updated on 28/Feb/20

$${find}\:{the}\:{derivtive}\:{of}\:{y}={e}^{\mathrm{cos}\:{x}} \\ $$
Commented by niroj last updated on 28/Feb/20

$$\:\:\:\mathrm{y}=\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} \\ $$$$\:\:\mathrm{D}.\mathrm{w}.\mathrm{r}.\mathrm{to}\:\mathrm{x}. \\ $$$$\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\:\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} \left(−\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\:−\mathrm{sin}\:\mathrm{x}\:.\mathrm{e}^{\mathrm{cos}\:\mathrm{x}} \\ $$
Commented by peter frank last updated on 28/Feb/20

$${lny}={lne}^{\mathrm{cos}\:{x}} \\ $$$${lny}=\mathrm{cos}\:{xlne} \\ $$$${lny}=\mathrm{cos}\:{x} \\ $$$$\frac{{y}^{'} }{{y}}=\mathrm{sin}\:\:{x} \\ $$$${y}^{'} ={y}\mathrm{sin}\:\:{x} \\ $$$${y}^{'} =−{e}^{\mathrm{cos}\:{x}} \mathrm{sin}\:{x} \\ $$
Answered by jagoll last updated on 28/Feb/20
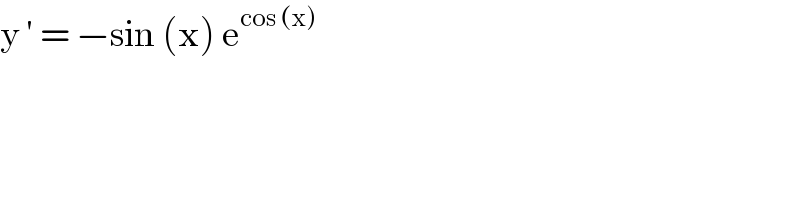
$$\mathrm{y}\:'\:=\:−\mathrm{sin}\:\left(\mathrm{x}\right)\:\mathrm{e}^{\mathrm{cos}\:\left(\mathrm{x}\right)} \: \\ $$
