Question Number 84100 by niroj last updated on 09/Mar/20
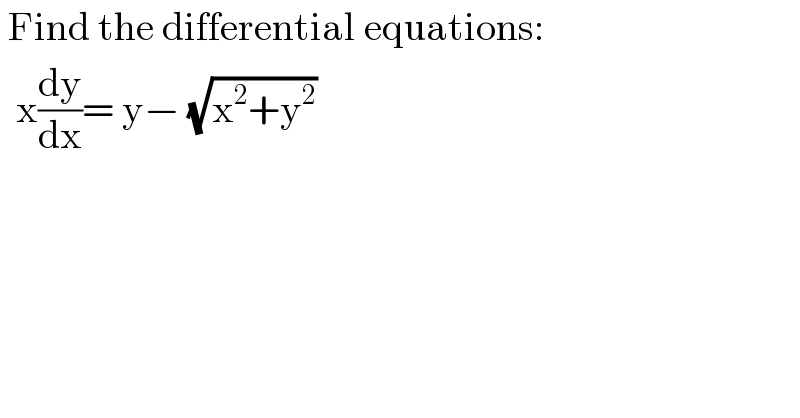
$$\:\mathrm{Find}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equations}: \\ $$$$\:\:\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}=\:\mathrm{y}−\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} } \\ $$
Answered by TANMAY PANACEA last updated on 09/Mar/20
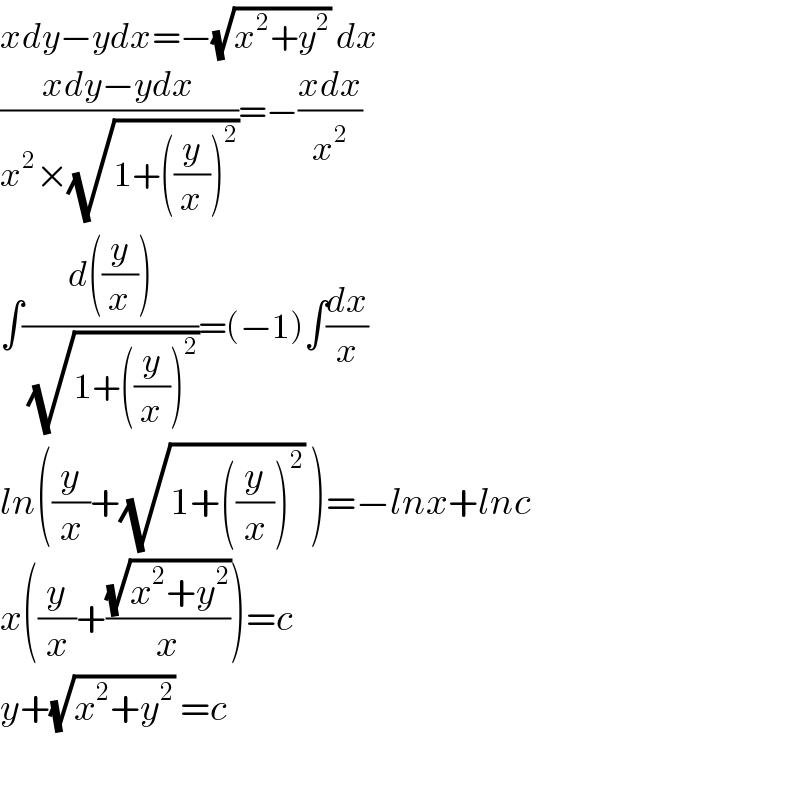
$${xdy}−{ydx}=−\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:{dx} \\ $$$$\frac{{xdy}−{ydx}}{{x}^{\mathrm{2}} ×\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }}=−\frac{{xdx}}{{x}^{\mathrm{2}} } \\ $$$$\int\frac{{d}\left(\frac{{y}}{{x}}\right)}{\:\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }}=\left(−\mathrm{1}\right)\int\frac{{dx}}{{x}} \\ $$$${ln}\left(\frac{{y}}{{x}}+\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:\right)=−{lnx}+{lnc} \\ $$$${x}\left(\frac{{y}}{{x}}+\frac{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}{{x}}\right)={c} \\ $$$${y}+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:={c} \\ $$$$ \\ $$
Commented by niroj last updated on 09/Mar/20

$${its}\:{great}\:. \\ $$
Answered by TANMAY PANACEA last updated on 09/Mar/20
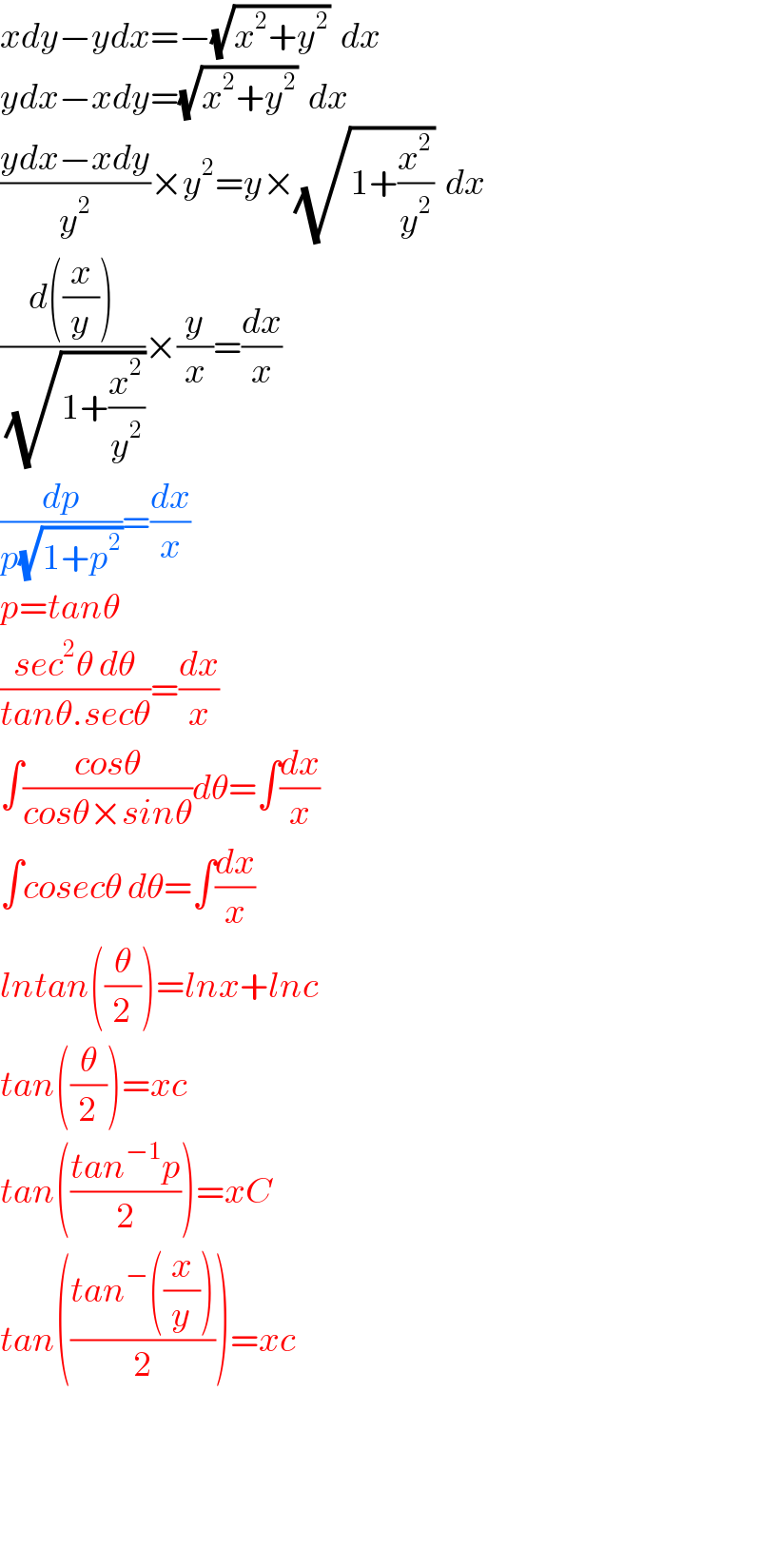
$${xdy}−{ydx}=−\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:{dx} \\ $$$${ydx}−{xdy}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:{dx} \\ $$$$\frac{{ydx}−{xdy}}{{y}^{\mathrm{2}} }×{y}^{\mathrm{2}} ={y}×\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }}\:\:{dx} \\ $$$$\frac{{d}\left(\frac{{x}}{{y}}\right)}{\:\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }}}×\frac{{y}}{{x}}=\frac{{dx}}{{x}} \\ $$$$\frac{{dp}}{{p}\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}=\frac{{dx}}{{x}} \\ $$$${p}={tan}\theta \\ $$$$\frac{{sec}^{\mathrm{2}} \theta\:{d}\theta}{{tan}\theta.{sec}\theta}=\frac{{dx}}{{x}} \\ $$$$\int\frac{{cos}\theta}{{cos}\theta×{sin}\theta}{d}\theta=\int\frac{{dx}}{{x}} \\ $$$$\int{cosec}\theta\:{d}\theta=\int\frac{{dx}}{{x}} \\ $$$${lntan}\left(\frac{\theta}{\mathrm{2}}\right)={lnx}+{lnc} \\ $$$${tan}\left(\frac{\theta}{\mathrm{2}}\right)={xc} \\ $$$${tan}\left(\frac{{tan}^{−\mathrm{1}} {p}}{\mathrm{2}}\right)={xC} \\ $$$${tan}\left(\frac{{tan}^{−} \left(\frac{{x}}{{y}}\right)}{\mathrm{2}}\right)={xc} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
