Question Number 123876 by john_santu last updated on 29/Nov/20

$${Find}\:{the}\:{distance}\:{from}\:{the}\: \\ $$$${point}\:{S}\left(\mathrm{1},\mathrm{1},\mathrm{5}\right)\:{to}\:{the}\:{line}\: \\ $$$${L}\::\:\begin{cases}{{x}=\mathrm{1}+{t}}\\{{y}=\mathrm{3}−{t}\:}\\{{z}=\mathrm{2}{t}}\end{cases}. \\ $$
Answered by mr W last updated on 29/Nov/20
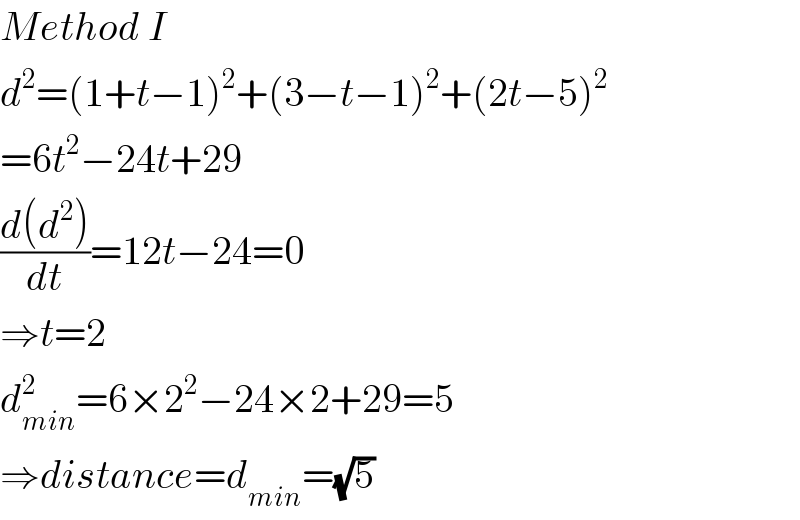
$${Method}\:{I} \\ $$$${d}^{\mathrm{2}} =\left(\mathrm{1}+{t}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{3}−{t}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}{t}−\mathrm{5}\right)^{\mathrm{2}} \\ $$$$=\mathrm{6}{t}^{\mathrm{2}} −\mathrm{24}{t}+\mathrm{29} \\ $$$$\frac{{d}\left({d}^{\mathrm{2}} \right)}{{dt}}=\mathrm{12}{t}−\mathrm{24}=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{2} \\ $$$${d}_{{min}} ^{\mathrm{2}} =\mathrm{6}×\mathrm{2}^{\mathrm{2}} −\mathrm{24}×\mathrm{2}+\mathrm{29}=\mathrm{5} \\ $$$$\Rightarrow{distance}={d}_{{min}} =\sqrt{\mathrm{5}} \\ $$
Answered by mr W last updated on 29/Nov/20
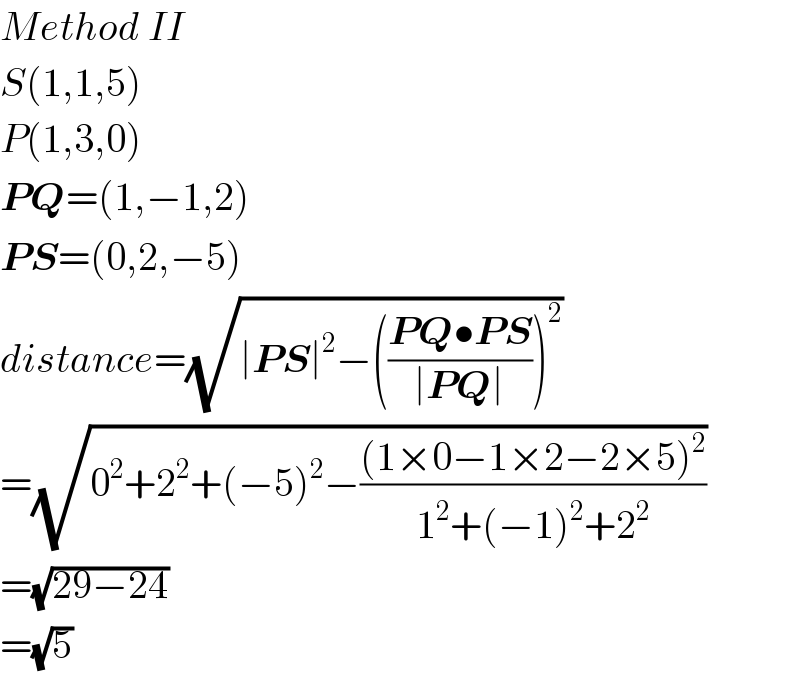
$${Method}\:{II} \\ $$$${S}\left(\mathrm{1},\mathrm{1},\mathrm{5}\right) \\ $$$${P}\left(\mathrm{1},\mathrm{3},\mathrm{0}\right) \\ $$$$\boldsymbol{{PQ}}=\left(\mathrm{1},−\mathrm{1},\mathrm{2}\right) \\ $$$$\boldsymbol{{PS}}=\left(\mathrm{0},\mathrm{2},−\mathrm{5}\right) \\ $$$${distance}=\sqrt{\mid\boldsymbol{{PS}}\mid^{\mathrm{2}} −\left(\frac{\boldsymbol{{PQ}}\bullet\boldsymbol{{PS}}}{\mid\boldsymbol{{PQ}}\mid}\right)^{\mathrm{2}} } \\ $$$$=\sqrt{\mathrm{0}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\left(−\mathrm{5}\right)^{\mathrm{2}} −\frac{\left(\mathrm{1}×\mathrm{0}−\mathrm{1}×\mathrm{2}−\mathrm{2}×\mathrm{5}\right)^{\mathrm{2}} }{\mathrm{1}^{\mathrm{2}} +\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }} \\ $$$$=\sqrt{\mathrm{29}−\mathrm{24}} \\ $$$$=\sqrt{\mathrm{5}} \\ $$
Answered by mr W last updated on 29/Nov/20
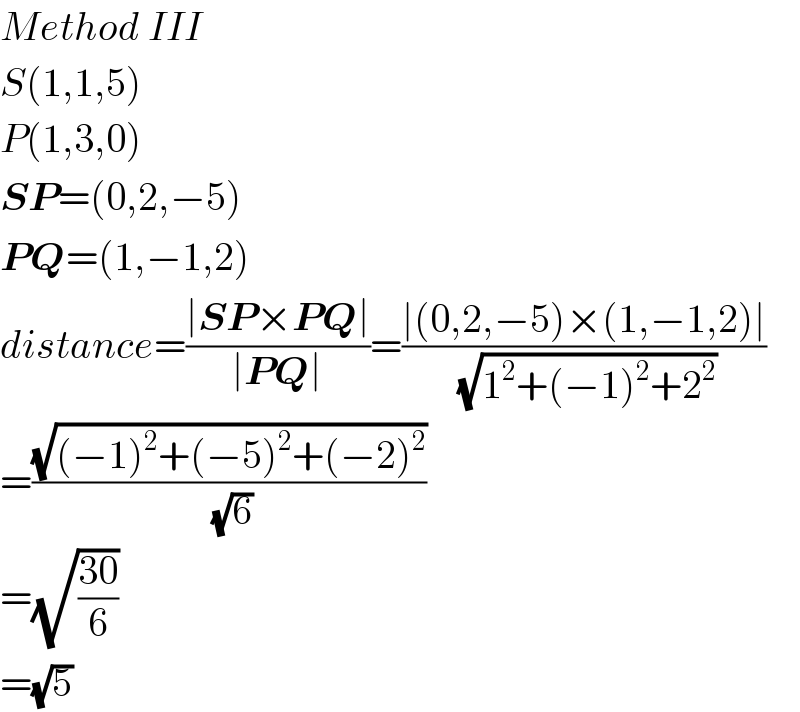
$${Method}\:{III} \\ $$$${S}\left(\mathrm{1},\mathrm{1},\mathrm{5}\right) \\ $$$${P}\left(\mathrm{1},\mathrm{3},\mathrm{0}\right) \\ $$$$\boldsymbol{{SP}}=\left(\mathrm{0},\mathrm{2},−\mathrm{5}\right) \\ $$$$\boldsymbol{{PQ}}=\left(\mathrm{1},−\mathrm{1},\mathrm{2}\right) \\ $$$${distance}=\frac{\mid\boldsymbol{{SP}}×\boldsymbol{{PQ}}\mid}{\mid\boldsymbol{{PQ}}\mid}=\frac{\mid\left(\mathrm{0},\mathrm{2},−\mathrm{5}\right)×\left(\mathrm{1},−\mathrm{1},\mathrm{2}\right)\mid}{\:\sqrt{\mathrm{1}^{\mathrm{2}} +\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }} \\ $$$$=\frac{\sqrt{\left(−\mathrm{1}\right)^{\mathrm{2}} +\left(−\mathrm{5}\right)^{\mathrm{2}} +\left(−\mathrm{2}\right)^{\mathrm{2}} }}{\:\sqrt{\mathrm{6}}} \\ $$$$=\sqrt{\frac{\mathrm{30}}{\mathrm{6}}} \\ $$$$=\sqrt{\mathrm{5}} \\ $$
