Menu Close

find-the-distance-of-point-2-1-2-to-plane-passing-through-points-1-2-3-0-4-2-and-1-3-4-

Tinku Tara 0 Comments
Pin




Question Number 118747 by bemath last updated on 19/Oct/20
find the distance of point (2,1,−2) to plane passing through points (−1,2,−3); (0,−4,−2) and (1,3,4).
$${find}\:{the}\:{distance}\:{of}\:{point}\:\left(\mathrm{2},\mathrm{1},−\mathrm{2}\right)\:{to}\:{plane} \\ $$$${passing}\:{through}\:{points}\:\left(−\mathrm{1},\mathrm{2},−\mathrm{3}\right); \\ $$$$\left(\mathrm{0},−\mathrm{4},−\mathrm{2}\right)\:{and}\:\left(\mathrm{1},\mathrm{3},\mathrm{4}\right). \\ $$
Answered by benjo_mathlover last updated on 19/Oct/20
Equation of plane passing through points (x_1 ,y_1 ,z_1 );(x_2 ,y_2 ,z_2 ); (x_3 ,y_3 ,z_3 ) is determinant (((x−x_1 y−y_1 z−z_1 )),((x_2 −x_1 y_2 −y_1 z_2 −z_1 )),((x_3 −x_1 y_3 −y_1 z_3 −z_1 )))= 0 so we get equation of plane is determinant (((x+1 y−2 z+3)),(( 1 −6 1 )),(( 2 1 7)))= 0 (x+1)(−43)−(y−2)(5)+(z+3)(13) = 0 −43x−43−5y+10+13z+39 = 0 ⇒43x+5y−13z−6=0 We want to compute the distance of point (2,1,−2) to plane 43x+5y−13z−6=0 by the formula ⇒d = ((∣43(2)+5(1)−13(−2)−6 ∣)/( (√(43^2 +5^2 +(−13)^2 )))) ⇒d = ((111)/( (√(2043))))
$${Equation}\:{of}\:{plane}\:{passing}\:{through}\:{points} \\ $$$$\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} ,{z}_{\mathrm{1}} \right);\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} ,{z}_{\mathrm{2}} \right);\:\left({x}_{\mathrm{3}} ,{y}_{\mathrm{3}} ,{z}_{\mathrm{3}} \right)\:{is}\: \\ $$$$\begin{vmatrix}{{x}−{x}_{\mathrm{1}} \:\:\:\:\:{y}−{y}_{\mathrm{1}} \:\:\:\:\:\:{z}−{z}_{\mathrm{1}} }\\{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} \:\:\:{y}_{\mathrm{2}} −{y}_{\mathrm{1}} \:\:\:\:{z}_{\mathrm{2}} −{z}_{\mathrm{1}} }\\{{x}_{\mathrm{3}} −{x}_{\mathrm{1}} \:\:\:{y}_{\mathrm{3}} −{y}_{\mathrm{1}} \:\:\:\:{z}_{\mathrm{3}} −{z}_{\mathrm{1}} }\end{vmatrix}=\:\mathrm{0} \\ $$$${so}\:{we}\:{get}\:{equation}\:{of}\:{plane}\:{is}\: \\ $$$$\begin{vmatrix}{{x}+\mathrm{1}\:\:\:\:\:{y}−\mathrm{2}\:\:\:\:\:\:{z}+\mathrm{3}}\\{\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:−\mathrm{6}\:\:\:\:\:\:\:\:\:\mathrm{1}\:}\\{\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{7}}\end{vmatrix}=\:\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left(−\mathrm{43}\right)−\left({y}−\mathrm{2}\right)\left(\mathrm{5}\right)+\left({z}+\mathrm{3}\right)\left(\mathrm{13}\right)\:=\:\mathrm{0} \\ $$$$−\mathrm{43}{x}−\mathrm{43}−\mathrm{5}{y}+\mathrm{10}+\mathrm{13}{z}+\mathrm{39}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{43}{x}+\mathrm{5}{y}−\mathrm{13}{z}−\mathrm{6}=\mathrm{0} \\ $$$${We}\:{want}\:{to}\:{compute}\:{the}\:{distance}\:{of}\: \\ $$$${point}\:\left(\mathrm{2},\mathrm{1},−\mathrm{2}\right)\:{to}\:{plane}\:\mathrm{43}{x}+\mathrm{5}{y}−\mathrm{13}{z}−\mathrm{6}=\mathrm{0} \\ $$$${by}\:{the}\:{formula}\:\Rightarrow{d}\:=\:\frac{\mid\mathrm{43}\left(\mathrm{2}\right)+\mathrm{5}\left(\mathrm{1}\right)−\mathrm{13}\left(−\mathrm{2}\right)−\mathrm{6}\:\mid}{\:\sqrt{\mathrm{43}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} +\left(−\mathrm{13}\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow{d}\:=\:\frac{\mathrm{111}}{\:\sqrt{\mathrm{2043}}}\: \\ $$
Answered by 1549442205PVT last updated on 19/Oct/20
Suppose A(−1,2,−3),B(0,−4,−2) C(1,3,4)⇒AB^(→) =(1,−6,1),AC^(→) =(2,1,7) The normal vector of the plane P is n^→ =AB^(→) ×AC^(→) =( (((−6),1),(1,7) ) , ((1,1),(7,2) ), ((1,(−6)),(2,1) )) =(−43,−5,13).Therefore,the equation of P pass through A(−1,2,−3) with the normal n^(→) =(−44,−5,13)is: −43(x+1)−5(y−2)+13(z+3)=0 ⇔−43x−5y+13z+6=0 The distance from the pointM (2,1,−2) to P is MH=((∣−43.2−5.1+13(−2)+6∣)/( (√(43^2 +5^2 +13^2 )))) =((111)/(3(√(227))))
$$\mathrm{Suppose}\:\mathrm{A}\left(−\mathrm{1},\mathrm{2},−\mathrm{3}\right),\mathrm{B}\left(\mathrm{0},−\mathrm{4},−\mathrm{2}\right) \\ $$$$\mathrm{C}\left(\mathrm{1},\mathrm{3},\mathrm{4}\right)\Rightarrow\overset{\rightarrow} {\mathrm{AB}}=\left(\mathrm{1},−\mathrm{6},\mathrm{1}\right),\overset{\rightarrow} {\mathrm{AC}}=\left(\mathrm{2},\mathrm{1},\mathrm{7}\right) \\ $$$$\mathrm{The}\:\mathrm{normal}\:\mathrm{vector}\:\mathrm{of}\:\mathrm{the}\:\mathrm{plane}\:\mathrm{P}\:\mathrm{is} \\ $$$$\overset{\rightarrow} {\mathrm{n}}=\overset{\rightarrow} {\mathrm{AB}}×\overset{\rightarrow} {\mathrm{AC}}=\left(\begin{pmatrix}{−\mathrm{6}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{7}}\end{pmatrix}\:,\begin{pmatrix}{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{7}}&{\mathrm{2}}\end{pmatrix},\begin{pmatrix}{\mathrm{1}}&{−\mathrm{6}}\\{\mathrm{2}}&{\mathrm{1}}\end{pmatrix}\right) \\ $$$$=\left(−\mathrm{43},−\mathrm{5},\mathrm{13}\right).\mathrm{Therefore},\mathrm{the}\:\mathrm{equation}\:\mathrm{of} \\ $$$$\mathrm{P}\:\mathrm{pass}\:\mathrm{through}\:\mathrm{A}\left(−\mathrm{1},\mathrm{2},−\mathrm{3}\right)\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{normal}\:\overset{\rightarrow} {\mathrm{n}}=\left(−\mathrm{44},−\mathrm{5},\mathrm{13}\right)\mathrm{is}: \\ $$$$−\mathrm{43}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{5}\left(\mathrm{y}−\mathrm{2}\right)+\mathrm{13}\left(\mathrm{z}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Leftrightarrow−\mathrm{43x}−\mathrm{5y}+\mathrm{13z}+\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{The}\:\mathrm{distance}\:\mathrm{from}\:\mathrm{the}\:\mathrm{pointM}\:\left(\mathrm{2},\mathrm{1},−\mathrm{2}\right) \\ $$$$\mathrm{to}\:\mathrm{P}\:\mathrm{is}\:\mathrm{MH}=\frac{\mid−\mathrm{43}.\mathrm{2}−\mathrm{5}.\mathrm{1}+\mathrm{13}\left(−\mathrm{2}\right)+\mathrm{6}\mid}{\:\sqrt{\mathrm{43}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} +\mathrm{13}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{111}}{\mathrm{3}\sqrt{\mathrm{227}}} \\ $$
Answered by mr W last updated on 19/Oct/20
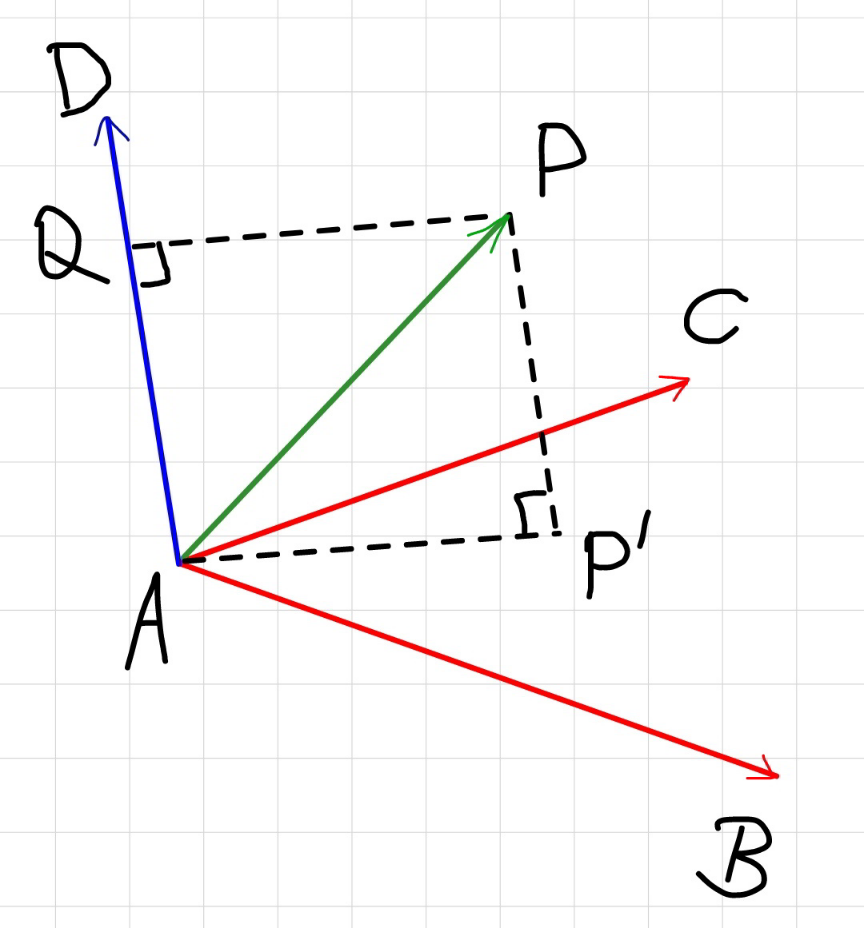
Commented by mr W last updated on 19/Oct/20
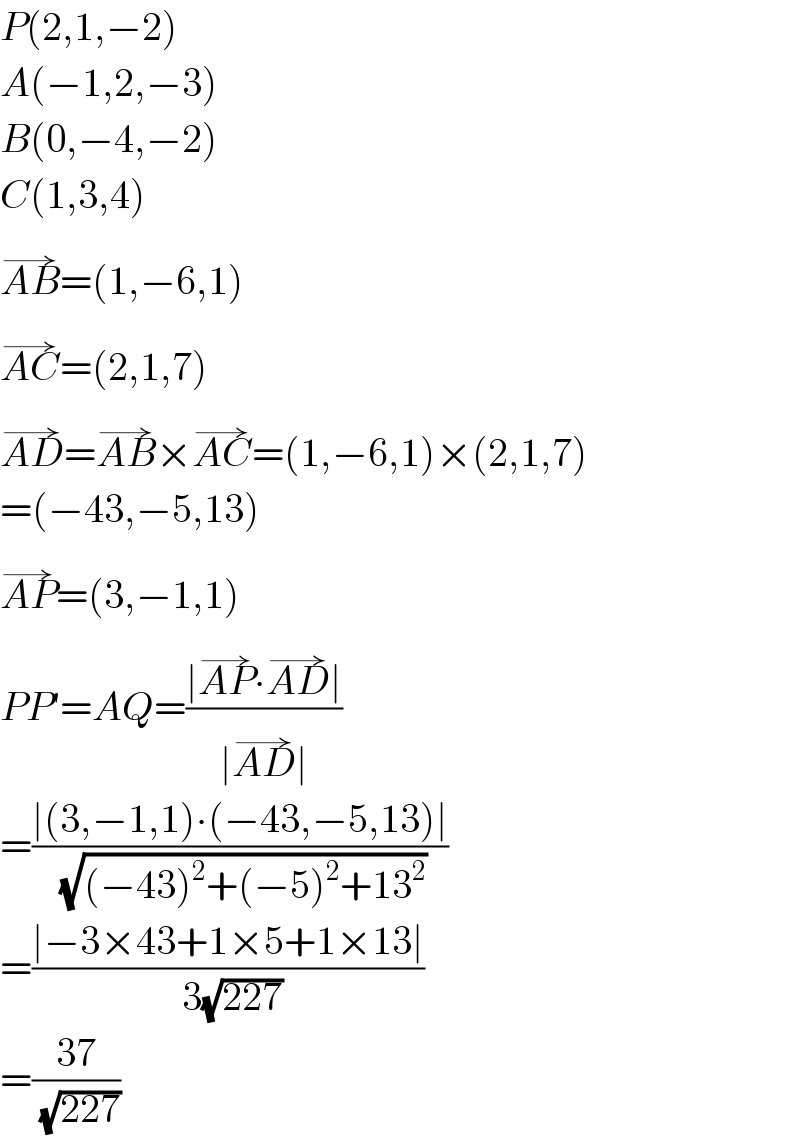
P(2,1,−2) A(−1,2,−3) B(0,−4,−2) C(1,3,4) AB^(→) =(1,−6,1) AC^(→) =(2,1,7) AD^(→) =AB^(→) ×AC^(→) =(1,−6,1)×(2,1,7) =(−43,−5,13) AP^(→) =(3,−1,1) PP′=AQ=((∣AP^(→) ∙AD^(→) ∣)/(∣AD^(→) ∣)) =((∣(3,−1,1)∙(−43,−5,13)∣)/( (√((−43)^2 +(−5)^2 +13^2 )))) =((∣−3×43+1×5+1×13∣)/( 3(√(227)))) =((37)/( (√(227))))
$${P}\left(\mathrm{2},\mathrm{1},−\mathrm{2}\right) \\ $$$${A}\left(−\mathrm{1},\mathrm{2},−\mathrm{3}\right) \\ $$$${B}\left(\mathrm{0},−\mathrm{4},−\mathrm{2}\right) \\ $$$${C}\left(\mathrm{1},\mathrm{3},\mathrm{4}\right) \\ $$$$\overset{\rightarrow} {{AB}}=\left(\mathrm{1},−\mathrm{6},\mathrm{1}\right) \\ $$$$\overset{\rightarrow} {{AC}}=\left(\mathrm{2},\mathrm{1},\mathrm{7}\right) \\ $$$$\overset{\rightarrow} {{AD}}=\overset{\rightarrow} {{AB}}×\overset{\rightarrow} {{AC}}=\left(\mathrm{1},−\mathrm{6},\mathrm{1}\right)×\left(\mathrm{2},\mathrm{1},\mathrm{7}\right) \\ $$$$=\left(−\mathrm{43},−\mathrm{5},\mathrm{13}\right) \\ $$$$\overset{\rightarrow} {{AP}}=\left(\mathrm{3},−\mathrm{1},\mathrm{1}\right) \\ $$$${PP}'={AQ}=\frac{\mid\overset{\rightarrow} {{AP}}\centerdot\overset{\rightarrow} {{AD}}\mid}{\mid\overset{\rightarrow} {{AD}}\mid} \\ $$$$=\frac{\mid\left(\mathrm{3},−\mathrm{1},\mathrm{1}\right)\centerdot\left(−\mathrm{43},−\mathrm{5},\mathrm{13}\right)\mid}{\:\sqrt{\left(−\mathrm{43}\right)^{\mathrm{2}} +\left(−\mathrm{5}\right)^{\mathrm{2}} +\mathrm{13}^{\mathrm{2}} }} \\ $$$$=\frac{\mid−\mathrm{3}×\mathrm{43}+\mathrm{1}×\mathrm{5}+\mathrm{1}×\mathrm{13}\mid}{\:\mathrm{3}\sqrt{\mathrm{227}}} \\ $$$$=\frac{\mathrm{37}}{\:\sqrt{\mathrm{227}}} \\ $$
Answered by ajfour last updated on 19/Oct/20
OA=−i+2j−3k OB=−4j−2k OC=i+3j+4k AB= i−6j+k ; BC=i+7j+6k n^� =AB×BC = determinant ((i,j,k),(1,(−6),1),(1,7,6)) = −43i−5j+13k distance of P (2,1,−2) we first find AP = 3i−j+k . Now = ((AP.n^� )/(∣n^� ∣)) = ∣(((3i−j+k).(−43i−5j+13k))/( (√(43^2 +5^2 +13^2 ))))∣ = ((∣−129+5+13∣)/( (√(2043)))) = ((111)/( (√(2043)))) = ((37)/( (√(227)))) .
$${OA}=−{i}+\mathrm{2}{j}−\mathrm{3}{k} \\ $$$${OB}=−\mathrm{4}{j}−\mathrm{2}{k} \\ $$$${OC}={i}+\mathrm{3}{j}+\mathrm{4}{k} \\ $$$$ \\ $$$${AB}=\:{i}−\mathrm{6}{j}+{k}\:\:\:;\:\:{BC}={i}+\mathrm{7}{j}+\mathrm{6}{k} \\ $$$$\bar {{n}}\:={AB}×{BC}\:=\begin{vmatrix}{{i}}&{{j}}&{{k}}\\{\mathrm{1}}&{−\mathrm{6}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{7}}&{\mathrm{6}}\end{vmatrix} \\ $$$$\:\:\:=\:−\mathrm{43}{i}−\mathrm{5}{j}+\mathrm{13}{k} \\ $$$${distance}\:{of}\:{P}\:\left(\mathrm{2},\mathrm{1},−\mathrm{2}\right)\:\:{we}\:{first} \\ $$$${find}\:{AP}\:=\:\mathrm{3}{i}−{j}+{k}\:\:.\:{Now} \\ $$$$\:\:\:=\:\:\frac{{AP}.\bar {{n}}}{\mid\bar {{n}}\mid}\:=\:\mid\frac{\left(\mathrm{3}{i}−{j}+{k}\right).\left(−\mathrm{43}{i}−\mathrm{5}{j}+\mathrm{13}{k}\right)}{\:\sqrt{\mathrm{43}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} +\mathrm{13}^{\mathrm{2}} }}\mid \\ $$$$\:\:\:=\:\frac{\mid−\mathrm{129}+\mathrm{5}+\mathrm{13}\mid}{\:\sqrt{\mathrm{2043}}}\:=\:\frac{\mathrm{111}}{\:\sqrt{\mathrm{2043}}}\:\:=\:\frac{\mathrm{37}}{\:\sqrt{\mathrm{227}}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *