Question Number 30017 by jonah last updated on 15/Feb/18

$$\mathrm{find}\:\mathrm{the}\:\mathrm{elements}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ellipse}\:\mathrm{given}\:\mathrm{the}\:\mathrm{following}\:\mathrm{equation} \\ $$$$\mathrm{1}.\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{25}}+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{1} \\ $$$$\mathrm{2}.\mathrm{x}^{\mathrm{2}} +\mathrm{9y}^{\mathrm{2}} =\mathrm{9} \\ $$
Answered by ajfour last updated on 15/Feb/18
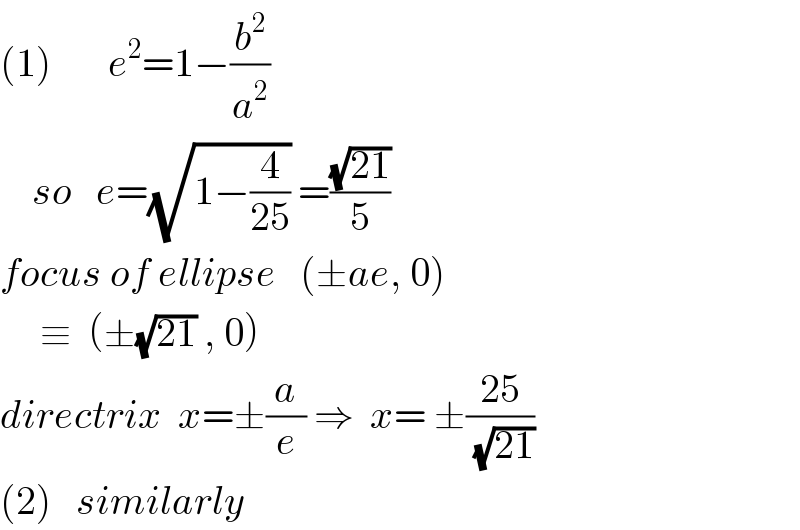
$$\left(\mathrm{1}\right)\:\:\:\:\:\:\:{e}^{\mathrm{2}} =\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} } \\ $$$$\:\:\:\:{so}\:\:\:{e}=\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{25}}}\:=\frac{\sqrt{\mathrm{21}}}{\mathrm{5}} \\ $$$${focus}\:{of}\:{ellipse}\:\:\:\left(\pm{ae},\:\mathrm{0}\right) \\ $$$$\:\:\:\:\:\equiv\:\:\left(\pm\sqrt{\mathrm{21}}\:,\:\mathrm{0}\right) \\ $$$${directrix}\:\:{x}=\pm\frac{{a}}{{e}}\:\Rightarrow\:\:{x}=\:\pm\frac{\mathrm{25}}{\:\sqrt{\mathrm{21}}} \\ $$$$\left(\mathrm{2}\right)\:\:\:{similarly} \\ $$
