Menu Close

find-the-equation-of-a-pair-of-straight-lines-represented-by-given-equation-2x-2-5xy-3y-2-3x-19y-20-0-

Tinku Tara 0 Comments
Pin




Question Number 29770 by gyugfeet last updated on 12/Feb/18
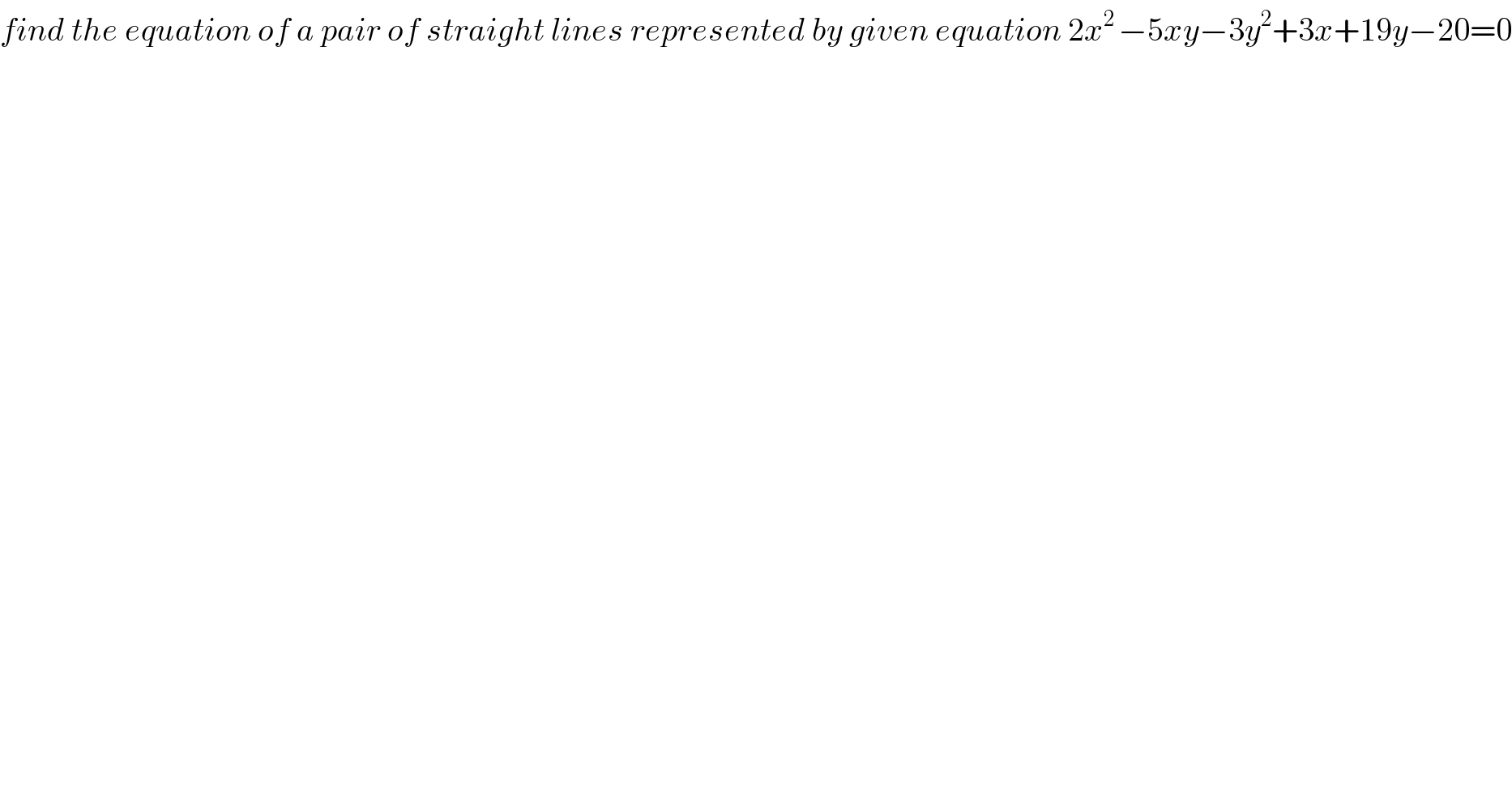
find the equation of a pair of straight lines represented by given equation 2x^(2 ) −5xy−3y^2 +3x+19y−20=0
$${find}\:{the}\:{equation}\:{of}\:{a}\:{pair}\:{of}\:{straight}\:{lines}\:{represented}\:{by}\:{given}\:{equation}\:\mathrm{2}{x}^{\mathrm{2}\:} −\mathrm{5}{xy}−\mathrm{3}{y}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{19}{y}−\mathrm{20}=\mathrm{0} \\ $$
Answered by ajfour last updated on 12/Feb/18
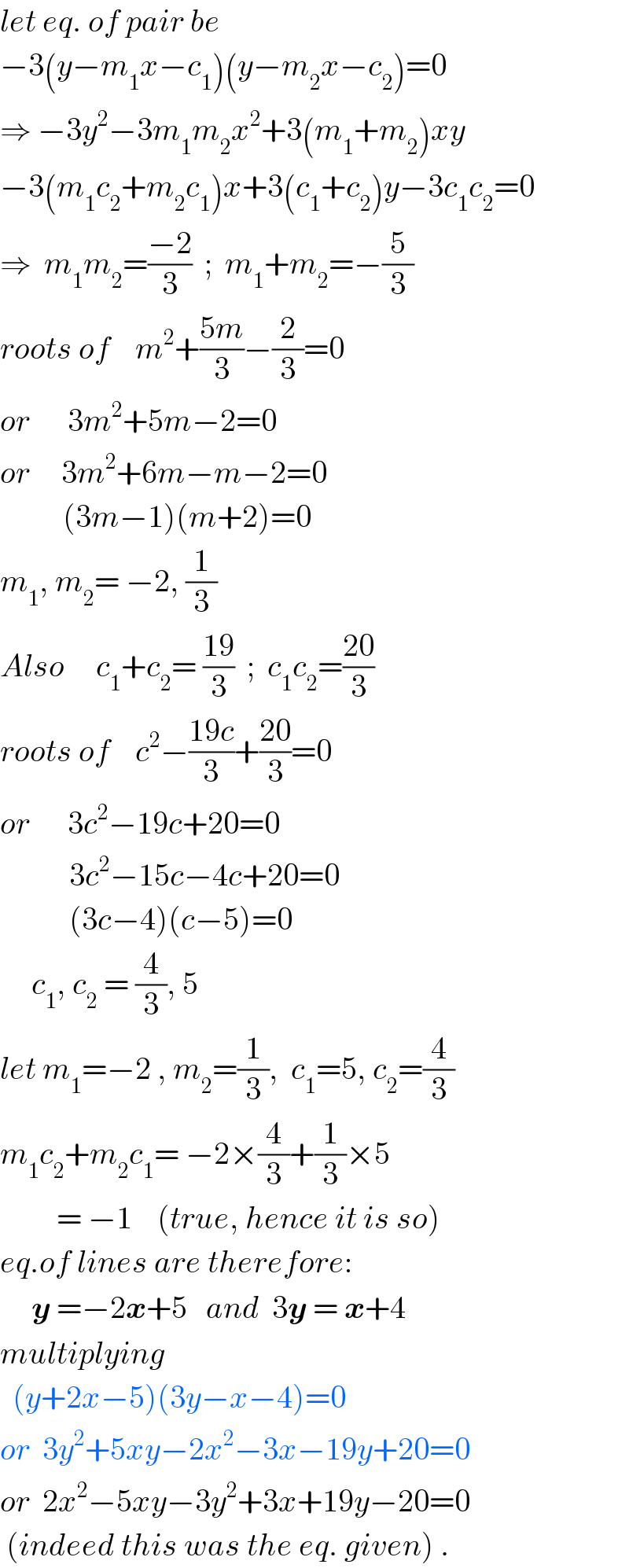
let eq. of pair be −3(y−m_1 x−c_1 )(y−m_2 x−c_2 )=0 ⇒ −3y^2 −3m_1 m_2 x^2 +3(m_1 +m_2 )xy −3(m_1 c_2 +m_2 c_1 )x+3(c_1 +c_2 )y−3c_1 c_2 =0 ⇒ m_1 m_2 =((−2)/3) ; m_1 +m_2 =−(5/3) roots of m^2 +((5m)/3)−(2/3)=0 or 3m^2 +5m−2=0 or 3m^2 +6m−m−2=0 (3m−1)(m+2)=0 m_1 , m_2 = −2, (1/3) Also c_1 +c_2 = ((19)/3) ; c_1 c_2 =((20)/3) roots of c^2 −((19c)/3)+((20)/3)=0 or 3c^2 −19c+20=0 3c^2 −15c−4c+20=0 (3c−4)(c−5)=0 c_1 , c_2 = (4/3), 5 let m_1 =−2 , m_2 =(1/3), c_1 =5, c_2 =(4/3) m_1 c_2 +m_2 c_1 = −2×(4/3)+(1/3)×5 = −1 (true, hence it is so) eq.of lines are therefore: y =−2x+5 and 3y = x+4 multiplying (y+2x−5)(3y−x−4)=0 or 3y^2 +5xy−2x^2 −3x−19y+20=0 or 2x^2 −5xy−3y^2 +3x+19y−20=0 (indeed this was the eq. given) .
$${let}\:{eq}.\:{of}\:{pair}\:{be} \\ $$$$−\mathrm{3}\left({y}−{m}_{\mathrm{1}} {x}−{c}_{\mathrm{1}} \right)\left({y}−{m}_{\mathrm{2}} {x}−{c}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:−\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{m}_{\mathrm{1}} {m}_{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{3}\left({m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right){xy} \\ $$$$−\mathrm{3}\left({m}_{\mathrm{1}} {c}_{\mathrm{2}} +{m}_{\mathrm{2}} {c}_{\mathrm{1}} \right){x}+\mathrm{3}\left({c}_{\mathrm{1}} +{c}_{\mathrm{2}} \right){y}−\mathrm{3}{c}_{\mathrm{1}} {c}_{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:{m}_{\mathrm{1}} {m}_{\mathrm{2}} =\frac{−\mathrm{2}}{\mathrm{3}}\:\:;\:\:{m}_{\mathrm{1}} +{m}_{\mathrm{2}} =−\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${roots}\:{of}\:\:\:\:{m}^{\mathrm{2}} +\frac{\mathrm{5}{m}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{0} \\ $$$${or}\:\:\:\:\:\:\mathrm{3}{m}^{\mathrm{2}} +\mathrm{5}{m}−\mathrm{2}=\mathrm{0} \\ $$$${or}\:\:\:\:\:\mathrm{3}{m}^{\mathrm{2}} +\mathrm{6}{m}−{m}−\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}{m}−\mathrm{1}\right)\left({m}+\mathrm{2}\right)=\mathrm{0} \\ $$$${m}_{\mathrm{1}} ,\:{m}_{\mathrm{2}} =\:−\mathrm{2},\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${Also}\:\:\:\:\:{c}_{\mathrm{1}} +{c}_{\mathrm{2}} =\:\frac{\mathrm{19}}{\mathrm{3}}\:\:;\:\:{c}_{\mathrm{1}} {c}_{\mathrm{2}} =\frac{\mathrm{20}}{\mathrm{3}} \\ $$$${roots}\:{of}\:\:\:\:{c}^{\mathrm{2}} −\frac{\mathrm{19}{c}}{\mathrm{3}}+\frac{\mathrm{20}}{\mathrm{3}}=\mathrm{0} \\ $$$${or}\:\:\:\:\:\:\mathrm{3}{c}^{\mathrm{2}} −\mathrm{19}{c}+\mathrm{20}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}{c}^{\mathrm{2}} −\mathrm{15}{c}−\mathrm{4}{c}+\mathrm{20}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}{c}−\mathrm{4}\right)\left({c}−\mathrm{5}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:{c}_{\mathrm{1}} ,\:{c}_{\mathrm{2}} \:=\:\frac{\mathrm{4}}{\mathrm{3}},\:\mathrm{5} \\ $$$${let}\:{m}_{\mathrm{1}} =−\mathrm{2}\:,\:{m}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}},\:\:{c}_{\mathrm{1}} =\mathrm{5},\:{c}_{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${m}_{\mathrm{1}} {c}_{\mathrm{2}} +{m}_{\mathrm{2}} {c}_{\mathrm{1}} =\:−\mathrm{2}×\frac{\mathrm{4}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:=\:−\mathrm{1}\:\:\:\:\left({true},\:{hence}\:{it}\:{is}\:{so}\right) \\ $$$${eq}.{of}\:{lines}\:{are}\:{therefore}: \\ $$$$\:\:\:\:\:\boldsymbol{{y}}\:=−\mathrm{2}\boldsymbol{{x}}+\mathrm{5}\:\:\:{and}\:\:\mathrm{3}\boldsymbol{{y}}\:=\:\boldsymbol{{x}}+\mathrm{4} \\ $$$${multiplying}\: \\ $$$$\:\:\left({y}+\mathrm{2}{x}−\mathrm{5}\right)\left(\mathrm{3}{y}−{x}−\mathrm{4}\right)=\mathrm{0} \\ $$$${or}\:\:\mathrm{3}{y}^{\mathrm{2}} +\mathrm{5}{xy}−\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{19}{y}+\mathrm{20}=\mathrm{0} \\ $$$${or}\:\:\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{xy}−\mathrm{3}{y}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{19}{y}−\mathrm{20}=\mathrm{0} \\ $$$$\:\left({indeed}\:{this}\:{was}\:{the}\:{eq}.\:{given}\right)\:. \\ $$
Answered by puneet1789 last updated on 12/Feb/18

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *