Menu Close

find-the-equation-of-a-parabola-with-focus-3-3-and-directrix-y-0-

Tinku Tara 0 Comments
Pin




Question Number 88378 by Rio Michael last updated on 10/Apr/20
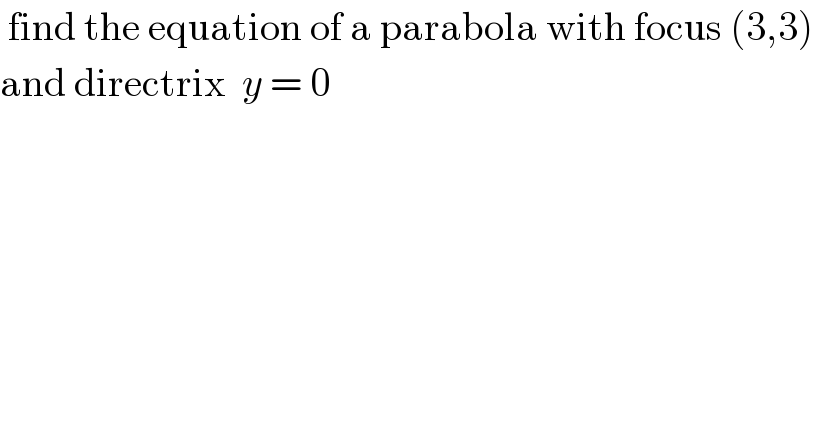
find the equation of a parabola with focus (3,3) and directrix y = 0
$$\:\mathrm{find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{a}\:\mathrm{parabola}\:\mathrm{with}\:\mathrm{focus}\:\left(\mathrm{3},\mathrm{3}\right) \\ $$$$\mathrm{and}\:\mathrm{directrix}\:\:{y}\:=\:\mathrm{0} \\ $$
Commented by john santu last updated on 10/Apr/20
o yes. should be a vertex at (3, (3/2))
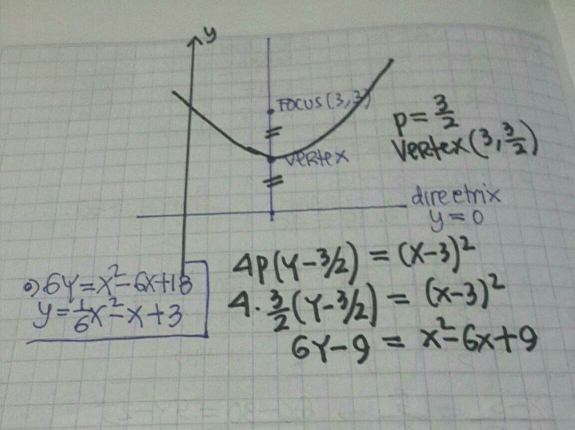
$${o}\:{yes}.\:{should}\:{be}\:{a}\:{vertex}\: \\ $$$${at}\:\left(\mathrm{3},\:\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Commented by john santu last updated on 10/Apr/20
Commented by john santu last updated on 10/Apr/20
focus (a, b+p) = (3,3) ⇒ { ((a=3)),((b+p = 3)) :} directrix y = b−p = 0 , b=p b = p = (3/2) equation of a parabola (x−3)^2 = 4.((3/2))(y−(3/2)) (x−3)^2 = 6 (y−(3/2))= 6y−9
$${focus}\:\left({a},\:{b}+{p}\right)\:=\:\left(\mathrm{3},\mathrm{3}\right)\:\Rightarrow\begin{cases}{{a}=\mathrm{3}}\\{{b}+{p}\:=\:\mathrm{3}}\end{cases} \\ $$$${directrix}\:{y}\:=\:{b}−{p}\:=\:\mathrm{0}\:,\:{b}={p} \\ $$$${b}\:=\:{p}\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${equation}\:{of}\:{a}\:{parabola} \\ $$$$\left({x}−\mathrm{3}\right)^{\mathrm{2}} \:=\:\mathrm{4}.\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\left({y}−\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\left({x}−\mathrm{3}\right)^{\mathrm{2}} \:=\:\mathrm{6}\:\left({y}−\frac{\mathrm{3}}{\mathrm{2}}\right)=\:\mathrm{6}{y}−\mathrm{9} \\ $$
Commented by mr W last updated on 10/Apr/20
correct
$${correct} \\ $$
Answered by mr W last updated on 10/Apr/20
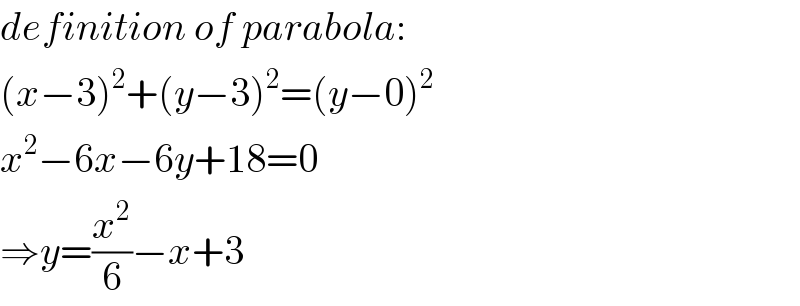
definition of parabola: (x−3)^2 +(y−3)^2 =(y−0)^2 x^2 −6x−6y+18=0 ⇒y=(x^2 /6)−x+3
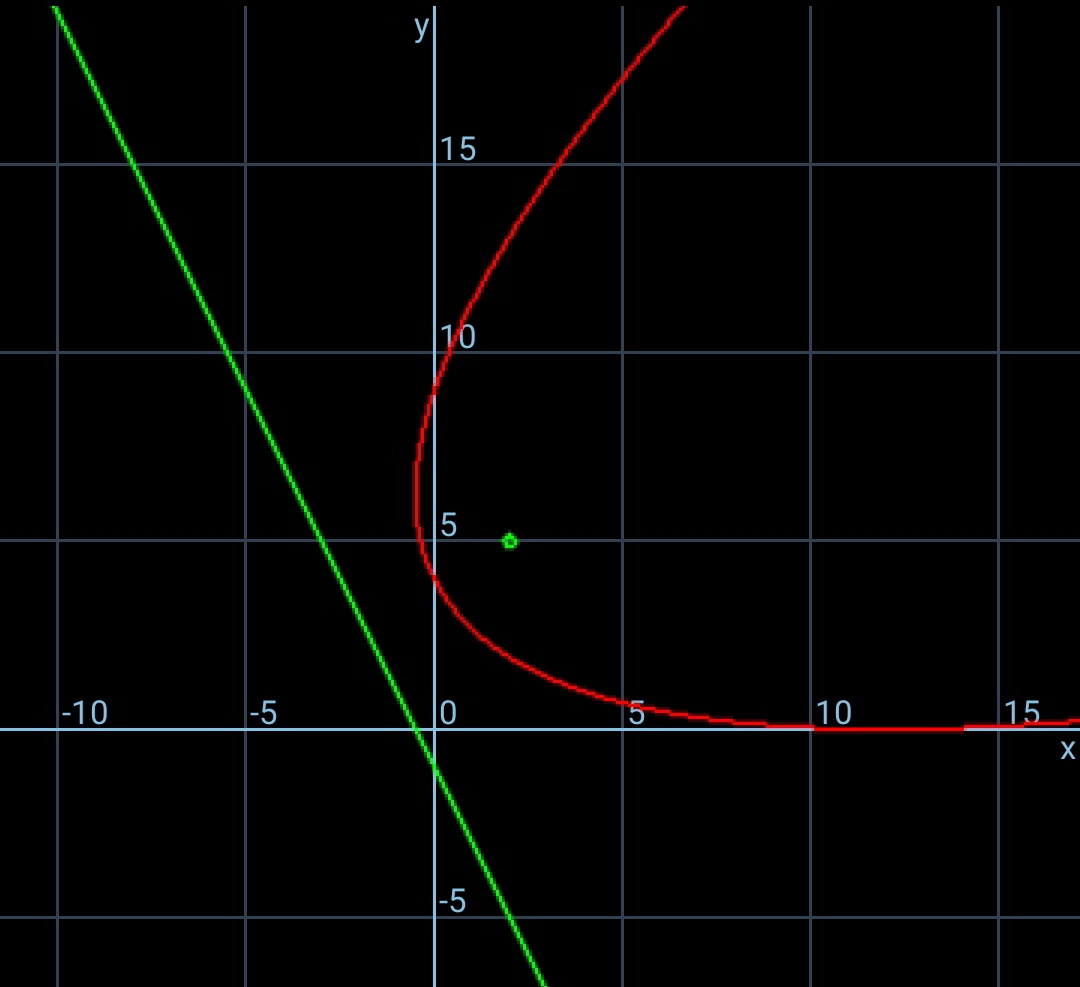
$${definition}\:{of}\:{parabola}: \\ $$$$\left({x}−\mathrm{3}\right)^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} =\left({y}−\mathrm{0}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{6}{y}+\mathrm{18}=\mathrm{0} \\ $$$$\Rightarrow{y}=\frac{{x}^{\mathrm{2}} }{\mathrm{6}}−{x}+\mathrm{3} \\ $$
Commented by jagoll last updated on 10/Apr/20
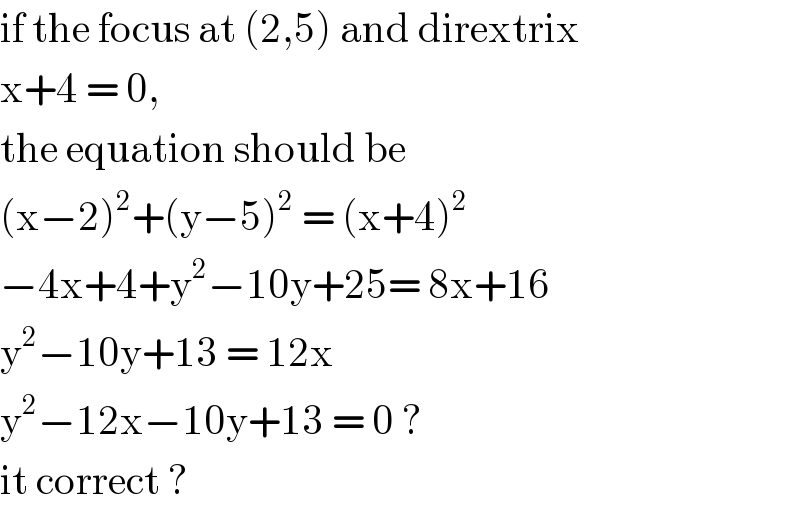
if the focus at (2,5) and dirextrix x+4 = 0, the equation should be (x−2)^2 +(y−5)^2 = (x+4)^2 −4x+4+y^2 −10y+25= 8x+16 y^2 −10y+13 = 12x y^2 −12x−10y+13 = 0 ? it correct ?
$$\mathrm{if}\:\mathrm{the}\:\mathrm{focus}\:\mathrm{at}\:\left(\mathrm{2},\mathrm{5}\right)\:\mathrm{and}\:\mathrm{dirextrix} \\ $$$$\mathrm{x}+\mathrm{4}\:=\:\mathrm{0},\: \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{should}\:\mathrm{be}\: \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{5}\right)^{\mathrm{2}} \:=\:\left(\mathrm{x}+\mathrm{4}\right)^{\mathrm{2}} \\ $$$$−\mathrm{4x}+\mathrm{4}+\mathrm{y}^{\mathrm{2}} −\mathrm{10y}+\mathrm{25}=\:\mathrm{8x}+\mathrm{16} \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{10y}+\mathrm{13}\:=\:\mathrm{12x} \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{12x}−\mathrm{10y}+\mathrm{13}\:=\:\mathrm{0}\:?\: \\ $$$$\mathrm{it}\:\mathrm{correct}\:? \\ $$
Commented by mr W last updated on 10/Apr/20
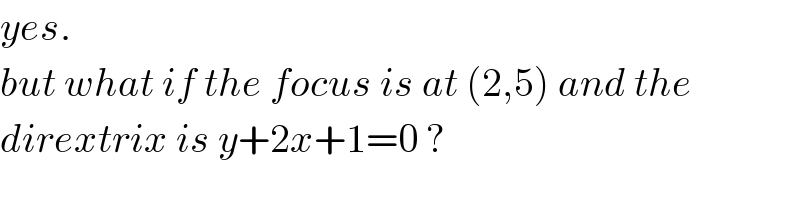
yes. but what if the focus is at (2,5) and the dirextrix is y+2x+1=0 ?
$${yes}. \\ $$$${but}\:{what}\:{if}\:{the}\:{focus}\:{is}\:{at}\:\left(\mathrm{2},\mathrm{5}\right)\:{and}\:{the} \\ $$$${dirextrix}\:{is}\:{y}+\mathrm{2}{x}+\mathrm{1}=\mathrm{0}\:? \\ $$
Commented by jagoll last updated on 10/Apr/20
does this matter wrong sir?
$$\mathrm{does}\:\mathrm{this}\:\mathrm{matter}\:\mathrm{wrong}\:\mathrm{sir}? \\ $$
Commented by mr W last updated on 10/Apr/20
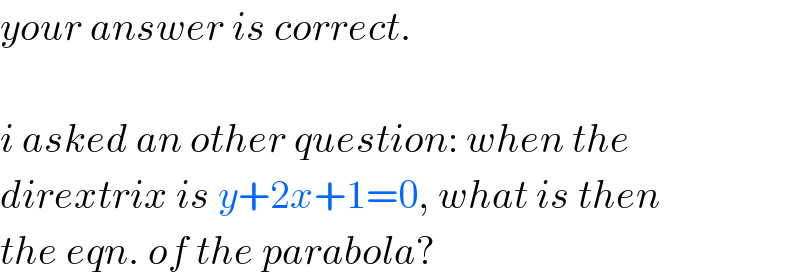
your answer is correct. i asked an other question: when the dirextrix is y+2x+1=0, what is then the eqn. of the parabola?
$${your}\:{answer}\:{is}\:{correct}. \\ $$$$ \\ $$$${i}\:{asked}\:{an}\:{other}\:{question}:\:{when}\:{the} \\ $$$${dirextrix}\:{is}\:{y}+\mathrm{2}{x}+\mathrm{1}=\mathrm{0},\:{what}\:{is}\:{then} \\ $$$${the}\:{eqn}.\:{of}\:{the}\:{parabola}? \\ $$
Commented by john santu last updated on 10/Apr/20
if focus at (2,5) and dirextrix is y+2x+1 = 0, we get p = (1/2)∣((5+4+1)/( (√5)))∣ p = (√5) , the line passes through focus orthogonal to dirextrix ⇒x−2y + 6=0 the parabola 4p(x−x_v )= (y−y_v )^2 by rotated θ = tan^(−1) ((1/2)). it correct
$${if}\:{focus}\:{at}\:\left(\mathrm{2},\mathrm{5}\right)\:{and}\:{dirextrix}\:{is} \\ $$$${y}+\mathrm{2}{x}+\mathrm{1}\:=\:\mathrm{0},\:{we}\:{get}\:{p}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mid\frac{\mathrm{5}+\mathrm{4}+\mathrm{1}}{\:\sqrt{\mathrm{5}}}\mid \\ $$$${p}\:=\:\sqrt{\mathrm{5}}\:,\:{the}\:{line}\:{passes}\:{through} \\ $$$${focus}\:{orthogonal}\:{to}\:{dirextrix} \\ $$$$\Rightarrow{x}−\mathrm{2}{y}\:+\:\mathrm{6}=\mathrm{0}\: \\ $$$${the}\:{parabola}\:\mathrm{4}{p}\left({x}−{x}_{{v}} \right)=\:\left({y}−{y}_{{v}} \right)^{\mathrm{2}} \\ $$$${by}\:{rotated}\:\theta\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right).\:{it}\:{correct} \\ $$
Commented by som(math1967) last updated on 10/Apr/20
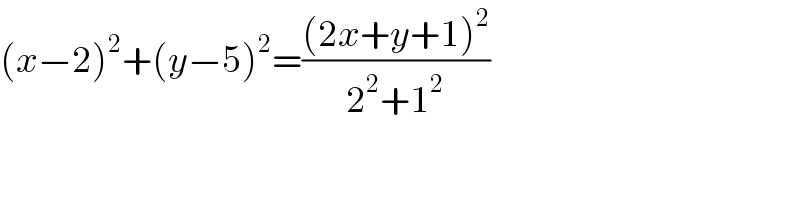
(x−2)^2 +(y−5)^2 =(((2x+y+1)^2 )/(2^2 +1^2 ))
$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\frac{\left(\mathrm{2}{x}+{y}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }\: \\ $$
Commented by mr W last updated on 10/Apr/20
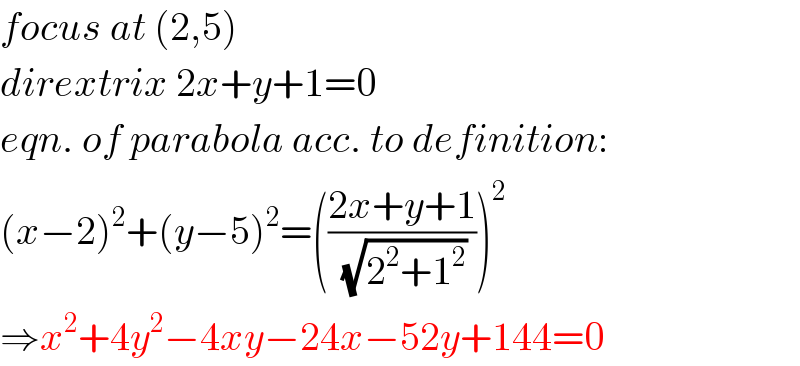
focus at (2,5) dirextrix 2x+y+1=0 eqn. of parabola acc. to definition: (x−2)^2 +(y−5)^2 =(((2x+y+1)/( (√(2^2 +1^2 )))))^2 ⇒x^2 +4y^2 −4xy−24x−52y+144=0
$${focus}\:{at}\:\left(\mathrm{2},\mathrm{5}\right) \\ $$$${dirextrix}\:\mathrm{2}{x}+{y}+\mathrm{1}=\mathrm{0} \\ $$$${eqn}.\:{of}\:{parabola}\:{acc}.\:{to}\:{definition}: \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\left(\frac{\mathrm{2}{x}+{y}+\mathrm{1}}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} −\mathrm{4}{xy}−\mathrm{24}{x}−\mathrm{52}{y}+\mathrm{144}=\mathrm{0} \\ $$
Commented by mr W last updated on 10/Apr/20
Commented by Rio Michael last updated on 10/Apr/20
wow am so grateful sirs
$$\mathrm{wow}\:\mathrm{am}\:\mathrm{so}\:\mathrm{grateful}\:\mathrm{sirs} \\ $$
Commented by john santu last updated on 10/Apr/20
how if the vertex parabola is (2,−1) and dirextrix y−2x+2=0 ?
$${how}\:{if}\:{the}\:{vertex}\:{parabola}\:{is}\: \\ $$$$\left(\mathrm{2},−\mathrm{1}\right)\:{and}\:{dirextrix}\:{y}−\mathrm{2}{x}+\mathrm{2}=\mathrm{0}\:? \\ $$$$ \\ $$
Commented by jagoll last updated on 10/Apr/20
great sir
$$\mathrm{great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *